今日主要总结一下动态规划0-1背包的一道题目，474. 一和零问题

题目：416. 分割等和子集

Leetcode题目地址
题目描述：
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。

请你找出并返回 strs 的最大子集的长度，该子集中 最多 有 m 个 0 和 n 个 1 。

如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。

示例 1：

输入：strs = [“10”, “0001”, “111001”, “1”, “0”], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {“10”,“0001”,“1”,“0”} ，因此答案是 4 。
其他满足题意但较小的子集包括 {“0001”,“1”} 和 {“10”,“1”,“0”} 。{“111001”} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。
示例 2：

输入：strs = [“10”, “0”, “1”], m = 1, n = 1
输出：2
解释：最大的子集是 {“0”, “1”} ，所以答案是 2 。

提示：

1 <= strs.length <= 600
1 <= strs[i].length <= 100
strs[i] 仅由 ‘0’ 和 ‘1’ 组成
1 <= m, n <= 100

本题重难点

首先本道题容易存在一个误区：该题并不是多重背包，而是0 - 1背包的问题！

多重背包是每个物品，数量不同的情况。

本题中strs 数组里的元素就是物品，每个物品都是一个！
而m 和 n相当于是一个背包，两个维度的背包。
理解成多重背包的同学主要是把m和n混淆为物品了，感觉这是不同数量的物品，所以以为是多重背包。

但本题其实是01背包问题！
这不过这个背包有两个维度，一个是m 一个是n，而不同长度的字符串就是不同大小的待装物品。
大家在做这道题之前最好看一下一文搞懂纯0-1背包问题我对0-1背包的基础理论知识有详细的讲解，本道题其实就是0-1 背包问题的应用，而这道题的难点主要在于怎么把一和零问题问题抽象成一个0-1 背包问题。

上一篇一文搞懂纯0-1背包问题文章我们讲过背包问题，大家都知道，有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。
要注意题目描述中商品是不是可以重复放入。

即一个商品如果可以重复多次放入是完全背包，而只能放入一次是0-1背包，写法还是不一样的。

要明确本题中我们要使用的是0-1背包，因为元素我们只能用一次。

开始动规五部曲：

1. 确定dp数组（dp table）以及下标的含义
   dp[i][j]：最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。

2. 确定递推公式
   dp[i][j] 可以由前一个strs里的字符串推导出来，strs里的字符串有x个0，y个1。
   dp[i][j] 就可以是 dp[i - x][j - y] + 1。
   然后我们在遍历的过程中，取dp[i][j]的最大值。
   所以递推公式：dp[i][j] = max(dp[i][j], dp[i - x][j - y] + 1);
   此时大家可以回想一下01背包的递推公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
   对比一下就会发现，字符串的x和y相当于物品的重量（weight[i]），字符串本身的个数相当于物品的价值（value[i]）,这个也是转化抽象成0 - 1背包问题的关键！！！ 这就是一个典型的01背包！ 只不过物品的重量有了两个维度而已。

3. dp数组如何初始化
   在动态规划：关于01背包问题，你该了解这些！（滚动数组） (opens new window)中已经讲解了，01背包的dp数组初始化为0就可以。
   因为物品价值不会是负数，初始为0，保证递推的时候dp[i][j]不会被初始值覆盖。

4. 确定遍历顺序
   在一文搞懂纯0-1背包问题中，我们讲了0 - 1背包为什么一定是外层for循环遍历物品，内层for循环遍历背包容量且从后向前遍历！
   那么本题也是，物品就是strs里的字符串，背包容量就是题目描述中的m和n。
   代码所示：

for (string str : strs) { // 遍历物品
    int x= 0, y= 0;
    for (char c : str) {
        if (c == '0') x++;
        else y++;
    }
    for (int i = m; i >= x; i--) { // 遍历背包容量且从后向前遍历！
        for (int j = n; j >= y; j--) {
            dp[i][j] = max(dp[i][j], dp[i - x][j - y] + 1);
        }
    }
}

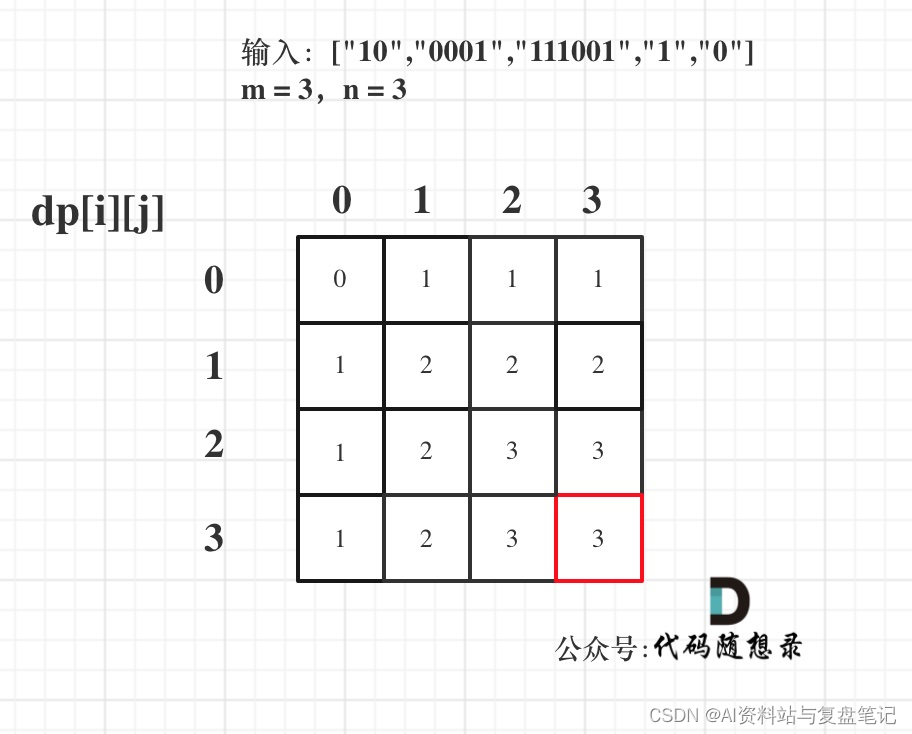
5. 举例推导dp数组

以输入：[“10”,“0001”,“111001”,“1”,“0”]，m = 3，n = 3为例 最后dp数组的状态如下所示：

C++代码

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        vector<vector<int>>dp(m + 1, vector<int>(n + 1, 0));
        for(auto& str : strs){
            int x = 0, y = 0;
            for(auto& s : str){
                if(s == '0') x++;
                else y++;
            }
            for(int i = m; i >= x; i--){
                for(int j = n; j >= y; j--){
                    dp[i][j] = max(dp[i][j], dp[i - x][j - y] + 1);
                }
            }
        }
        return dp[m][n];
    }
};

---

总结

动态规划
英文：Dynamic Programming，简称DP，如果某一问题有很多重叠子问题，使用动态规划是最有效的。
动态规划中每一个状态一定是由上一个状态推导出来的，这一点就区分于贪心，贪心没有状态推导，而是从局部直接选最优的

对于动态规划问题，可以拆解为如下五步曲，这五步都搞清楚了，才能说把动态规划真的掌握了！

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

这篇文章主要总结了一些动态规划解决一和零问题，依然是使用动规五部曲，做每道动态规划题目这五步都要弄清楚才能更清楚的理解题目！

不少同学刷过这道提，可能没有总结这究竟是什么背包。

此时我们讲解了0-1背包的多种应用，

1、纯 0 - 1 背包是求 给定背包容量 装满背包 的最大价值是多少。
2、416. 分割等和子集是求 给定背包容量，能不能装满这个背包。
3、1049. 最后一块石头的重量 II 是求 给定背包容量，尽可能装，最多能装多少
4、 494. 目标和 是求 给定背包容量，装满背包有多少种方法。 本题一和零问题是求 给定背包容量，装满背包最多有多少个物品。

欢迎大家关注本人公众号：编程复盘与思考随笔

(关注后可以免费获得本人在csdn发布的资源源码)