1、堆的基本概念
之前在学习优先级队列的时候, 学习到了堆的概念,现在重新回忆一下:
- 堆在逻辑上,是一颗完全二叉树
- 堆在物理上,是存储在数组中的
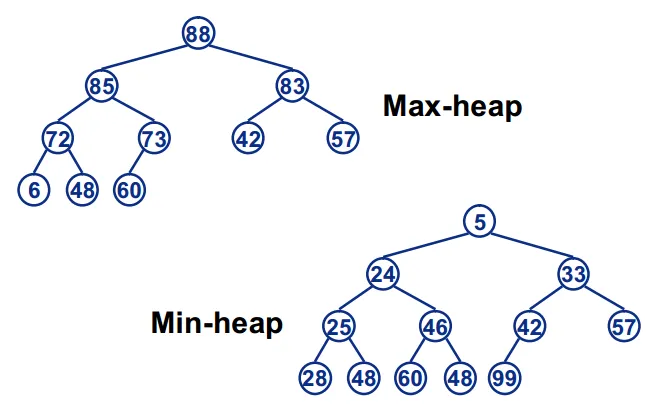
- 任意根节点值>=子树节点值,叫做大顶堆。
- 任意根节点值<=子树节点值,叫做小顶堆。
- 堆的基本作用是快速找到集合中的最值。
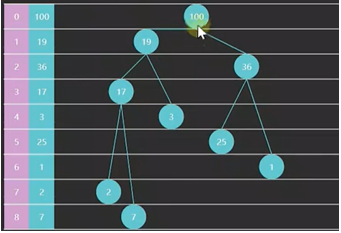
前置知识点:
从索引0开始存储节点数据有如下规律:
- 节点i的父节点索引为 floor((i-1)/2) ,i>0
- 节点i的左子节点为 2i+1,右子节点为 2i+2,当然索引都要小于堆容量size
2、堆的实现
1、节点的下沉操作
- 先找出当前节点的左右子节点
- 定义一个max值,代表节点数据最大的值的索引,赋初始值为parent节点
- 和左右节点分别比较(如果有子节点),更新max值
- 如果max值有改变,说明子节点比当前节点打,执行下沉操作
- 递归调动下沉操作
// 下沉操作
private void down(int parent) {
int left = parent * 2 + 1;
int right = left + 1;
int max = parent;
if (left < size && array[max] < array[left]) {
max = left;
}
if (right < size && array[max] < array[right]) {
max = right;
}
if (parent != max) {
swap(parent, max);
// 这里有个递归调用,跳出递归的条件就是parent == max
down(max);
}
}
// 交换操作
private void swap(int x, int y) {
int tmp = array[x];
array[x] = array[y];
array[y] = tmp;
}2、节点的上浮操作
- 计算出父节点的坐标index
- 当前节点和父节点进行比较,如果比父节点大,那么就执行上浮操作
- 循环1和2两个步骤,直到跳出循环。
private void up(int child) {
int parent = (child - 1) / 2;
while (parent >= 0 && array[parent] < array[child]) {
swap(parent, child);
child = parent;
parent = (child - 1) / 2;
}
}
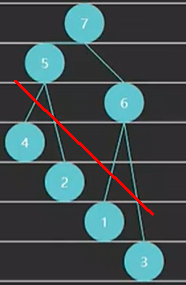
3、堆的构造方法 --- 建立堆的操作
找到堆中的最后一个非叶子节点,从当前节点往前遍历,不断的执行下沉操作

public void heapify() {
// 先找到最后一个非叶子节点(size/2-1),往前遍历,对每个节点执行下潜操作。
for (int i = size / 2 - 1; i >= 0; i--) {
down(i);
}
}4、取出堆顶元素
- 堆顶元素先用一个临时变量存储,便于返回
- 将堆顶元素和最后一个元素互换位置,这个时候,size-- 就相当于把堆顶元素移除了
- 此时新的堆顶元素不符合大顶堆的规律,执行下沉操作即可
移除指定元素的操作,思路也是一样的,代码如下:
// 移除堆顶部元素方法
public int poll() {
return poll(0);
}
// 移除指定位置元素方法
public int poll(int index) {
if (isEmpty() || index >= size || index < 0) {
return 0;
}
int removed = array[index];
swap(index, size - 1);
size--;
down(index);
return removed;
}5、添加新的元素
- 将新元素添加到最后的位置
- 对最后的位置进行上浮操作,然后size++;
如果数组满了,可以执行扩容,或者其他操作。
public boolean offer(int offered) {
if (isFull()) {
array = Arrays.copyOf(array, array.length*2);
}
array[size] = offered;
up(size);
size++;
return true;
}3、利用堆排序
算法描述:
- heapify 建立大顶堆
- 堆顶和堆底的元素交换顺序,缩小size并下沉调整堆
- 重复第二步,直到堆中只剩一个元素
其他排序方法:
前面已经实现了大顶堆,其实poll方法拿出来的,就是当前最大的元素,因此排序方法可以写成下面的格式。
// 倒叙排序 public int[] sort(int[] arr) { MaxHeap maxHeap = new MaxHeap(arr); int[] res = new int[maxHeap.size]; int count = 0; while (maxHeap.size > 0) { res[count] = maxHeap.poll(); count++; } return res; } // 正序排序 public int[] sort2(int[] arr) { MaxHeap maxHeap = new MaxHeap(arr); int[] res = new int[maxHeap.size]; int count = maxHeap.size - 1; while (maxHeap.size > 0) { res[count] = maxHeap.poll(); count--; } return res; }
215. 数组中的第K个最大元素
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
解题思路:
可以利用堆排序来求解:
- 使用小顶堆,先把数组前K个元素入队,这样堆顶的元素就是前K个元素中,第K个大的
- 从k+1个元素开始,与堆顶元素进行比较,如果比堆顶元素大,那么就替换堆顶元素,然后重新构建小顶堆
- 循环2步骤,循环完成,堆顶的元素就是所求的值。
// 借用PriorityQueue实现小顶堆 public int findKthLargest(int[] nums, int k) { PriorityQueue<Integer> queue = new PriorityQueue<>(); for (int i = 0; i < k; i++) { queue.offer(nums[i]); } for (int i = k; i < nums.length; i++) { if (nums[i] > queue.peek()) { // 这里replace方法更好,但是因为PriorityQueue没有这个方法, // 所以先出后入,效果一样,但是效率会降低 queue.poll(); queue.offer(nums[i]); } } return queue.peek(); }
703. 数据流中的第 K 大元素
题目比较难以理解,简单的说就是,给一个数组,和一个k的值,进行初始化,每次add的时候,加入一个元素,然后,把当前数据里面第K大的元素删除并返回。
解题思路:
- 定义一个小顶堆,可以用优先队列,存储前K大的元素,那么栈顶,就是第K大的元素。
- 加入元素到队列中,如果size大于k,那么就poll,保证队列中只有K个元素
- 返回堆顶的元素,就是本题的解。
class KthLargest { int k; PriorityQueue<Integer> queue; public KthLargest(int k, int[] nums) { this.k = k; queue = new PriorityQueue<>(); for (int num : nums) { queue.offer(num); } } public int add(int val) { queue.offer(val); while (queue.size() > k) { queue.poll(); } return queue.peek(); } }
295. 数据流的中位数
不断的往定义的列表中添加数据,取这个列表中的中位数
解题思路:
- 定义两个优先级队列,一个大顶堆,一个小顶堆
- 列表中的元素需要满足以下条件
- 两个优先级的队列中,元素之差不能超过1
- 大顶堆中的数据都是列表中值比较小的一半
- 小顶堆中的数据都是列表中值比较大的一半
实现代码:
- 添加元素时,要添加的元素和大顶堆中的堆顶元素对比,如果比他小,则添加到大顶堆中,否则,添加到小顶堆中
- 添加完元素,要平衡两个队列的元素数量,如果大顶堆的数据比小顶堆中的数据多2,那么就把大顶堆中堆顶的数据poll出来offer进小顶堆,反之亦然。
- 取中位数操作:如果队列数据是奇数,那么取元素较多的哪个堆的堆顶数据即可,如果为偶数,那么取两个堆顶数据求平均值。
public class MedianFinder { int sizeA; int sizeB; PriorityQueue<Integer> queue1; PriorityQueue<Integer> queue2; public MedianFinder() { this.sizeA = 0; this.sizeB = 0; // 大顶堆 queue1 = new PriorityQueue<>(new Comparator<Integer>() { @Override public int compare(Integer o1, Integer o2) { return o2 - o1; } }); // 小顶堆 queue2 = new PriorityQueue<>(new Comparator<Integer>() { @Override public int compare(Integer o1, Integer o2) { return o1 - o2; } }); } public void addNum(int num) { if (sizeA == 0) { queue1.offer(num); sizeA++; return; } if (queue1.peek() > num) { queue1.offer(num); sizeA++; if (sizeA - sizeB > 0) { queue2.offer(queue1.poll()); sizeA--; sizeB++; } } else { queue2.offer(num); sizeB++; if (sizeB - sizeA > 0) { queue1.offer(queue2.poll()); sizeB--; sizeA++; } } } public double findMedian() { double x; if (sizeA - sizeB == 1) { x = queue1.peek() * 1.0; } else if (sizeB - sizeA == 1) { x = queue2.peek() * 1.0; } else { x = (queue1.peek() + queue2.peek()) / 2.0; } return x; } public static void main(String[] args) { MedianFinder medianFinder = new MedianFinder(); medianFinder.addNum(40); System.out.println(medianFinder.findMedian()); medianFinder.addNum(12); System.out.println(medianFinder.findMedian()); medianFinder.addNum(16); System.out.println(medianFinder.findMedian()); } }本题代码是借用Java中的优先队列实现大顶堆和小顶堆。
提供一种更加简单的写法,但是效率会低一些
class MedianFinder { PriorityQueue<Integer> queue1; PriorityQueue<Integer> queue2; public MedianFinder() { // 大顶堆 queue1 = new PriorityQueue<>(new Comparator<Integer>() { @Override public int compare(Integer o1, Integer o2) { return o2 - o1; } }); // 小顶堆 queue2 = new PriorityQueue<>(new Comparator<Integer>() { @Override public int compare(Integer o1, Integer o2) { return o1 - o2; } }); } public void addNum(int num) { // 队列元素相等,就把元素加入到q1中,但是要先加q2,然后poll出来在加q1, if (queue1.size() == queue2.size()) { queue2.offer(num); queue1.offer(queue2.poll()); } // 队列元素不等,就把元素加到q2中,但是要先加入q1,然后poll出来在加q2, else { queue1.offer(num); queue2.offer(queue1.poll()); } } public double findMedian() { if (queue2.size() == queue1.size()) { return (queue2.peek() + queue1.peek()) / 2.0; } else { return queue1.peek(); } } }