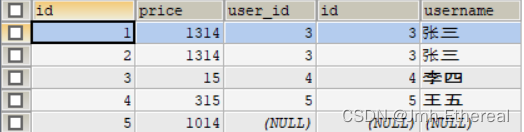
2022年深圳杯数学建模
D题 复杂水平井三维轨道设计
原题再现:
在油气田开采过程中,井眼轨迹直接影响着整个钻井整体效率。对于复杂水平井,较差的井眼轨迹很可能会造成卡钻或施加钻压困难等重大事故的发生。因而,在施工之前分析影响井眼轨迹走向规律的诸多因素,设计最适当的井眼轨迹显得十分重要。
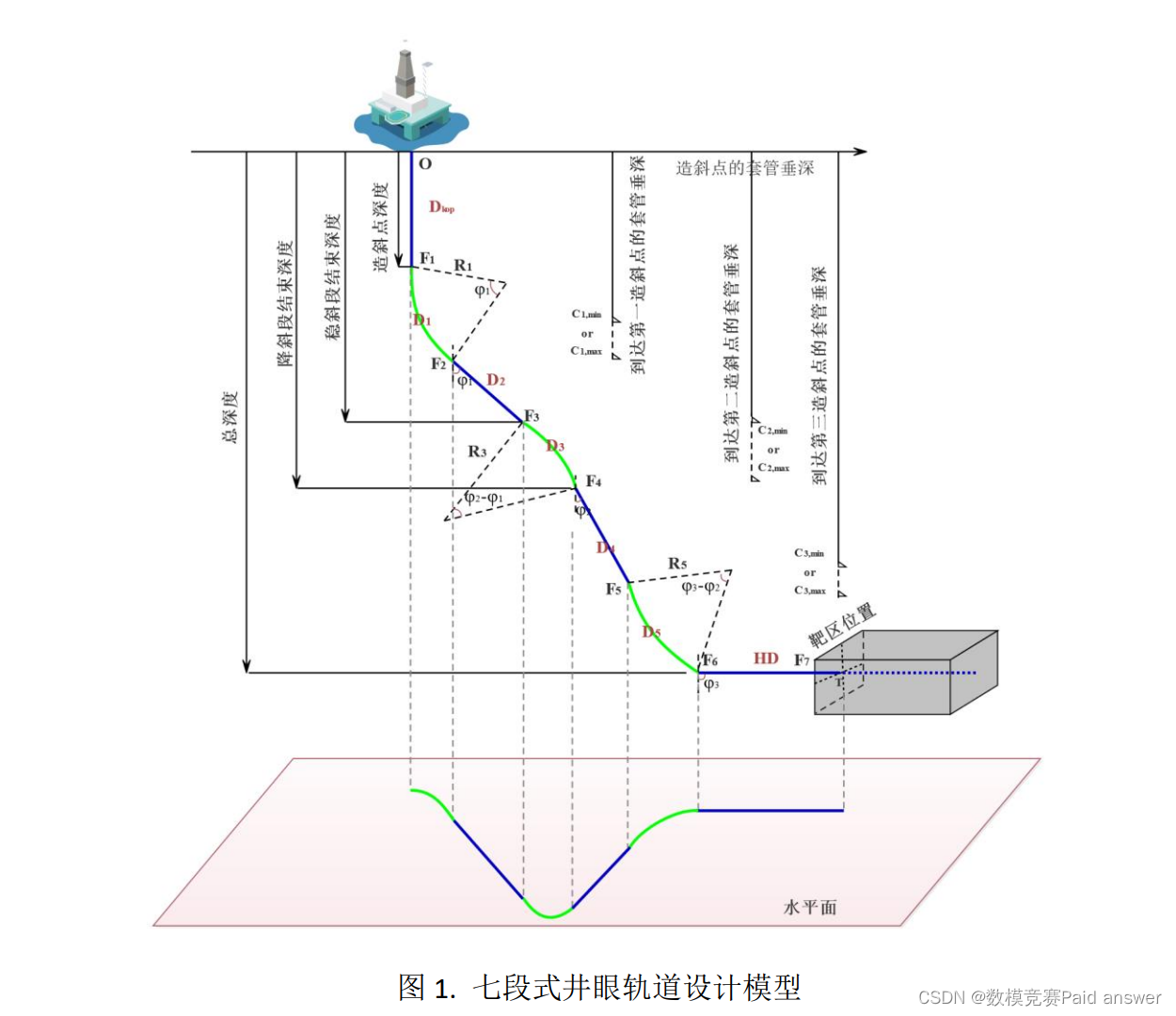
在井眼轨道设计模型中,设计轨道往往由一些连续的曲线构成。目前常用的复杂水平井的井眼轨道设计模型有“垂直段 + 增斜段 + 稳斜段 + 扭方位段 + 稳斜段 + 增斜段 + 水平段”的七段式井眼轨道设计模型,如图 1 所示。描述井眼轨道的参数可分为基本测斜参数、坐标参数、挠曲参数和工艺参数,基本测斜参数包括井深、井斜角、方位角;坐标参数用来确定轨道上一点的空间位置,在空间直角坐标系下,空间坐标可由北坐标、东坐标和垂深表示;挠曲参数主要指井眼轨道的曲率、挠率等参数;工艺参数是指钻井施工中用来确定井眼轨道的参数,主要包括造斜点、工具造斜率和工具面角。
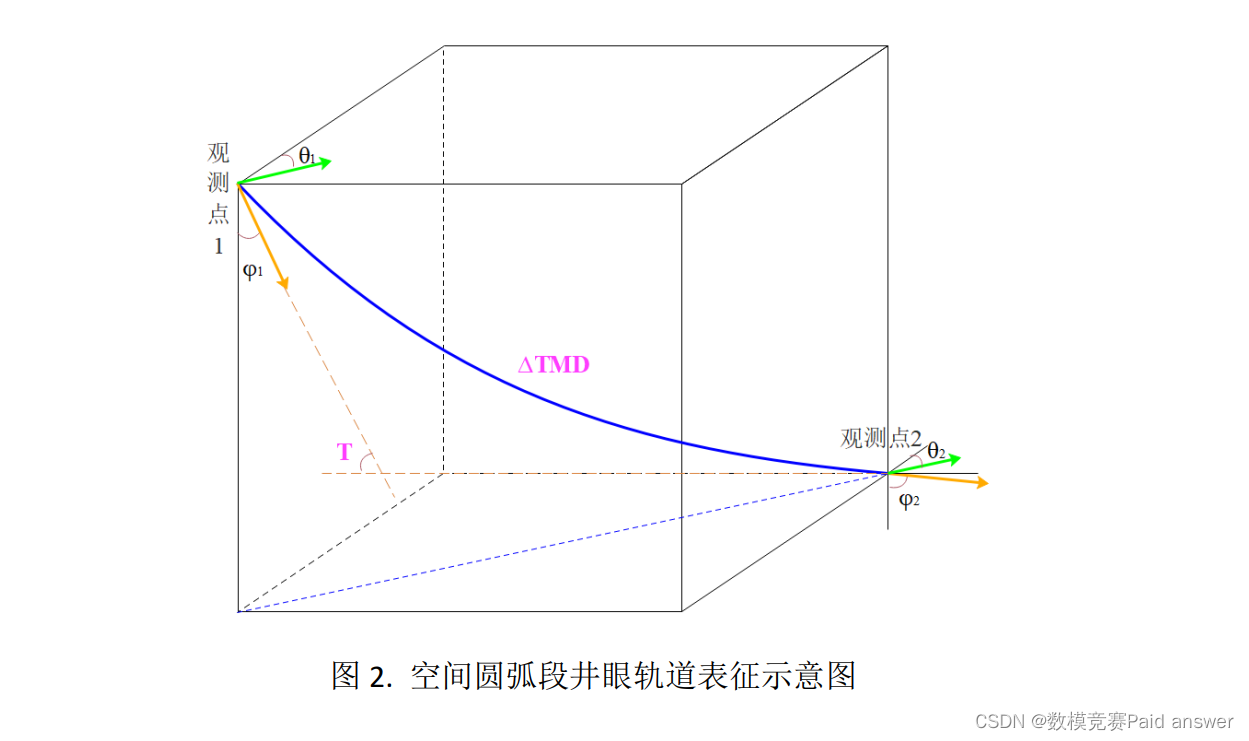
七段式井眼轨道设计模型由空间上的圆弧(如增斜段、扭方位段)和直线(如垂直段、稳斜段)构成,相邻曲线、直线之间光滑连接。对于井眼轨道设计模型的每个井段,通过表征三维井眼轨道所需要的特征参数将观测点 1 到观测点 2处确定井眼轨道的形状和姿态,如图 2 所示。图 2 中所示井段是由观测点 1 的方位角(𝜃1)和井斜角(𝜑1)、观测点 2 的方位角(𝜃2)和井斜角(𝜑2)以及狗腿度(𝑇)征成。狗腿度为从井眼内的一点到另一点,井眼前进方向变化的角度。狗腿度既反映了井斜角度的变化,又反映了方位角度的变化。
石油套管是用于支撑油、气井井壁的钢管,以保证完井后整个油井的正常运行。为此,套管坐封点应该位于合适的地层中,以便在固井后为套管鞋提供压力完整性。对于七段式井眼轨道设计模型,套管坐封点限制了井斜角的角度。为此,在设计时需要考虑套管坐封点的影响,如图 1 所示。
钻井公司作为采油厂的服务方,合理的完工验收标准是服务合同的要件。由于地层的复杂性,完全精准地按设计的井眼轨道完成钻井的可能性较小。如何平衡钻井成本和风险与完井采油的方便之间的冲突,提出一套合理的钻井完工验收标准也是本题目的任务之一。
请根据附录中的要求及相关参数建立模型解决以下问题:
1、以井段为研究对象,采用七段式井眼轨道设计模型,结合井眼轨道优化设计参数范围表,确定理想的井眼轨道模型。
2、对于复杂水平井来说,当管柱在井眼轨道中上下移动时,就会产生阻力。小的阻力和扭矩有助于获得光滑的井眼轨道。在问题 1 的基础上,考虑摩阻扭矩和阻力等情况下,确定理想的井眼轨道模型。
3、假设靶区窗口为长方形(如图 1 所示),靶心位于窗口中心处。由于测量的影响,井眼轨道定位不可能绝对准确。因此,在问题 2 的基础上,考虑命中率的情况,确定理想的井眼轨道模型。
4、通过平衡钻井成本和风险与完井采油的方便之间的冲突,试提出一套合理的水平井钻井完工验收标准。
模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:(代码和文档not free)
论文及程序仅供学习与参考
clc
ub=[1000 0.05 20/180*pi 1e4 280/180*pi 0.05 70/180*pi 1e4 340/180*pi 0.05 95/180*pi 2500
360/180*pi];
%
x0=[600.000000033230,0.0499925875432984,0.251281784577095,8135.87054070139,4.88689196614623,0.0499968793949498,0.703700778004902,2302.52301332556,5.86390402261779,0.0499978475987956,1.57079667653942,2500,6.19592152519464];
% bestans=inf;
% bestx=[];
% for i=1:100
% x0=lb.*ones(1,13)+rand(1,13).*(ub-lb);
% val=mubiao(x0);
% if val<bestans
% bestans=val;
% bestx=x;
% end
% end
x0=lb.*ones(1,13)+rand(1,13).*(ub-lb);
bestans=inf;
bestx=[];
x0=zeros(1,13);
x0=[600.000000435625,0.0499937835871316,0.277421869896148,8667.95585024487,4.88692132819307,0.0499968781918714,0.710782773523233,1908.33276341582,5.93167876542183,0.0499979250231581,1.57079902229204,2500,6.19592704860859];
x0=[600.000000004856,0.0498194123145741,0.246838160545951,6986.61336511958,4.88691243686372,0.0499998905363713,0.698133901959542,2895.70852760148,5.75984827430497,0.0480233512021104,1.57079632679508,lb(12),6.19591922750954];
%x0=[600.000000000474,0.0499922910852401,0.188439861671324,7807.56595163688,4.88093300907059,0.0499971437030730,0.698136879582935,2274.05305014408,5.75959558773011,0.0499360742110562,1.57079632679509,2500,6.19592428891987];
ans1=[];
for i=1:10
% x0=lb.*ones(1,13)+rand(1,13).*(ub-lb);
%
x0=[600.000000000474,0.0499922910852401,0.188439861671324,7807.56595163688,4.88093300907059,0.0499971437030730,0.698136879582935,2274.05305014408,5.75959558773011,0.0499360742110562,1.57079632679509,2500+(i-5)*10,6.19592428891987];
% lb=[600 0 10/180*pi 0 270/180*pi 0 40/180*pi 0 330/180*pi 0 90/180*pi 2500+(i-5)*10
355/180*pi];
% ub=[1000 0.05 20/180*pi 1e4 280/180*pi 0.05 70/180*pi 1e4 340/180*pi 0.05 95/180*pi
2500+(i-5)*10 360/180*pi];
option = optimoptions('fmincon','Algorithm','interior-point');
% option = optimoptions('fmincon','Algorithm','sqp');
% option = optimoptions('fmincon','Algorithm','active-set');
[x,fval] = fmincon(@mubiao,x0,[],[],[],[],lb,ub,@feixinxing,option);
fval
if fval<bestans
bestans=fval;
bestx=x;
end
ans1(i)=fval;
x0=x;
end
figure(2);
plot(2459,ans1(1),'w.');
hold on;
for i=1:10
plot(2500+(i-5)*10,ans1(i),'r*');
if i>1
line([2500+(i-6)*10 2500+(i-5)*10],[ans1(i-1) ans1(i)],'LineStyle','-','linewidth',1);
end
hold on;
end
r1=t2r(bestx(2),0,bestx(3),bestx(5),bestx(5)); %x(2)
r2=t2r(bestx(6),bestx(3),bestx(7),bestx(5),bestx(9)); %x(6)
r3=t2r(bestx(10),bestx(7),bestx(11),bestx(9),bestx(13)); %x(10)
o=[0 0 0];
disp(o);
f7=[5107.5 -3179 10875];
f1=o+[0 0 x(1)];
f2=f1+[r1*tan(x(3)/2)*sin(x(3))*cos(x(5)) r1*tan(x(3)/2)*sin(x(3))*sin(x(5)) r1*sin(x(3))];
f3=f2+[x(4)*sin(x(3))*cos(x(5)) x(4)*sin(x(3))*sin(x(5)) x(4)*cos(x(3))];
f4=f3+[r2*tan((x(7)-x(3))/2)*(sin(x(3))*cos(x(5))+sin(x(7))*cos(x(9)))
r2*tan((x(7)-x(3))/2)*(sin(x(3))*sin(x(5))+sin(x(7))*sin(x(9)))
r2*tan((x(7)-x(3))/2)*(cos(x(7))+cos(x(3)))];
f5=f4+[x(8)*sin(x(7))*cos(x(9)) x(8)*sin(x(7))*sin(x(9)) x(8)*cos(x(7))];
f6=f7-[x(12)*sin(x(11))*cos(x(13)) x(12)*sin(x(11))*sin(x(13)) x(12)*cos(x(11))];
disp(f1);f1(3)=-f1(3);temp=f1(2);f1(2)=f1(1);f1(1)=temp;
disp(f2);f2(3)=-f2(3);temp=f2(2);f2(2)=f2(1);f2(1)=temp;
disp(f3);f3(3)=-f3(3);temp=f3(2);f3(2)=f3(1);f3(1)=temp;
disp(f4);f4(3)=-f4(3);temp=f4(2);f4(2)=f4(1);f4(1)=temp;
disp(f5);f5(3)=-f5(3);temp=f5(2);f5(2)=f5(1);f5(1)=temp;
disp(f6);f6(3)=-f6(3);temp=f6(2);f6(2)=f6(1);f6(1)=temp;
disp(f7);f7(3)=-f7(3);temp=f7(2);f7(2)=f7(1);f7(1)=temp;
figure(1);
% xlim([o(1)-1000 f7(3)])
% ylim([-f7(3) 1000])
% zlim([o(3)-1000 f7(3)])
plot3(o(1),o(2),o(3),'k.','markersize',10);
hold on;
plot3(-500,500,-500,'w.');
plot3(f1(1),f1(2),f1(3),'k.','markersize',10);
line([o(1) f1(1)],[o(2) f1(2)],[o(3) f1(3)],'Color','blue','LineStyle','-','linewidth',2);
view(3);
plot3(f2(1),f2(2),f2(3),'k.','markersize',10);
plot3(f3(1),f3(2),f3(3),'k.','markersize',10);
plot3(f4(1),f4(2),f4(3),'k.','markersize',10);
line([f3(1) f2(1)],[f3(2) f2(2)],[f3(3) f2(3)],'Color','blue','LineStyle','-','linewidth',2);
view(3);
plot3(f5(1),f5(2),f5(3),'k.','markersize',10);
line([f4(1) f5(1)],[f4(2) f5(2)],[f4(3) f5(3)],'Color','blue','LineStyle','-','linewidth',2);
view(3);
plot3(f6(1),f6(2),f6(3),'k.','markersize',10);
plot3(f7(1),f7(2),f7(3),'k.','markersize',10);
line([f6(1) f7(1)],[f6(2) f7(2)],[f6(3) f7(3)],'Color','blue','LineStyle','-','linewidth',2);
view(3);
grid on
axis square
PathL(1)=pi*r1*x(3);
PathL(2)=pi*r2*(x(7)-x(3));
PathL(3)=pi*r3*(x(11)-x(7));
function f = mubiao(x)
r1=t2r(x(2),0,x(3),x(5),x(5)); %x(2)
r2=t2r(x(6),x(3),x(7),x(5),x(9)); %x(6)
r3=t2r(x(10),x(7),x(11),x(9),x(13)); %x(10)
f=x(1)+pi*r1*x(3)+x(4)+pi*r2*(x(7)-x(3))+x(8)+pi*r3*(x(11)-x(7))+x(12);
end
function [c,ceq] = feixinxing(x)
% 非线性不等式约束
T=0.05;
A=180/pi;
r1=t2r(x(2),0,x(3),x(5),x(5)); %x(2)
r2=t2r(x(6),x(3),x(7),x(5),x(9)); %x(6)
r3=t2r(x(10),x(7),x(11),x(9),x(13)); %x(10)
c = [x(1)+r1*sin(x(3))+x(4)*cos(x(3))-7000;
-x(1)-r1*sin(x(3))-x(4)*cos(x(3))+6000;
x(1)+r1*sin(x(3))+x(4)*cos(x(3))+r2*tan((x(7)-x(3))/2)*(cos(x(7))+cos(x(3)))+x(8)*cos(x(7))-10200;
-x(1)-r1*sin(x(3))-x(4)*cos(x(3))-r2*tan((x(7)-x(3))/2)*(cos(x(7))+cos(x(3)))-x(8)*cos(x(7))+10000;
x(1)+r1*sin(x(3))+x(4)*cos(x(3))+r2*tan((x(7)-x(3))/2)*(cos(x(7))+cos(x(3)))+x(8)*cos(x(7))+r3*tan((x(11)-x(7))/2)*(cos(x(11))+cos(x(7)))-10900;
-x(1)-r1*sin(x(3))-x(4)*cos(x(3))-r2*tan((x(7)-x(3))/2)*(cos(x(7))+cos(x(3)))-x(8)*cos(x(7))-r3*tan((x(11)-x(7))/2)*(cos(x(11))+cos(x(7)))+10850;
A*1/r1-T;
-A*1/r1;
A*1/r2*(x(7)-x(3))*sqrt((x(7)-x(3))^2+(x(9)-x(5))^2*sin((x(7)+x(3))/2)^2)-T ;
-A*1/r2*(x(7)-x(3))*sqrt((x(7)-x(3))^2+(x(9)-x(5))^2*sin((x(7)+x(3))/2)^2);
A*1/r3*(x(11)-x(7))*sqrt((x(11)-x(7))^2+(x(13)-x(9))^2*sin((x(11)+x(7))/2)^2)-T;
-A*1/r3*(x(11)-x(7))*sqrt((x(11)-x(7))^2+(x(13)-x(9))^2*sin((x(11)+x(7))/2)^2);
];
% 非线性等式约束
N7=5107.5;
E7=-3179;
H7=10875;
ceq = [
r1*tan(x(3)/2)*sin(x(3))*cos(x(5))+x(4)*sin(x(3))*cos(x(5))+r2*tan((x(7)-x(3))/2)*(sin(x(3))*cos(x(5))+sin(x(7))*cos(x(9)))+x(8)*sin(x(7))*cos(x(9))+r3*tan((x(11)-x(7))/2)*(sin(x(7))*cos(x(9))+sin(x(11))*cos(x(13)))+x(12)*sin(x(11))*cos(x(13))-N7
;
r1*tan(x(3)/2)*sin(x(3))*sin(x(5))+x(4)*sin(x(3))*sin(x(5))+r2*tan((x(7)-x(3))/2)*(sin(x(3))*sin(x(5))+sin(x(7))*sin(x(9)))+x(8)*sin(x(7))*sin(x(9))+r3*tan((x(11)-x(7))/2)*(sin(x(7))*sin(x(9))+sin(x(11))*sin(x(13)))+x(12)*sin(x(11))*sin(x(13))-E7
;
r1*sin(x(3))+x(4)*cos(x(3))+r2*tan((x(7)-x(3))/2)*(cos(x(3))+cos(x(7)))+x(8)*cos(x(7))+r3*tan((x(11)-x(7))/2)*(cos(x(7))+cos(x(11)))+x(12)*cos(x(11))-H7
];
end
function r = t2r(t,p1,p2,j1,j2)
r=180/(pi*t*(p2-p1))*sqrt((p2-p1)^2+(j2-j1)^2*sin((p1+p2)/2)^2);
end