哈希表（hash）

什么是hash？

散列,是把任意长度的输入通过散列算法变换成固定长度输出，该输出的值就是散列值。这种转换是一种压缩映射。映射表达的是一一对应的关系，也就是说，散列值的空间通常会小于输入空间。

const md5 = require('md5-node');
const password = 12345;
console.log(md5(password));

哈希算法不能从结果去推断输出，也就是说哈希算法是不可逆的。

哈希特性

不可逆，可以作为加密算法存在。
计算极快

MD5是不可逆的。对比方式进行校验，（web安全：彩虹表）

哈希用途

密码
文件完整校验

数组的不足：

如果是基于索引，数组性能好，但如果基于内容，性能就比较低（插入删除：链表性能好；查询修改：数组性能好）。

举个栗子

有800个好友，设计一个数据结构存储好友信息，名字、邮箱地址

链表查询慢，每次必须从头到尾遍历，用数组需要索引，增加id

const friend = [

{ id:1,name:'张三' ,email:'123@qq.com'},

{ id:2,name:'李四' ,email:'456@qq.com'},

]

有没有一个方法可以将名字直接作为索引提升查询速度？

将字符串name转换成数组的索引，这种东西叫哈希表。

哈希表通常是基于数组时限的，但相对于数组，优势：

它可以提供非常快的插入-删除-查找操作（哈希表的结构：数组，但是它和数组不同的是哈希表对于索引一种转换，我们称之为哈希函数）

例如：单词如何转化数字编码？

ASCLL码，编码方式可将字符转化成数字

哈希表是以键值对存储的数据结构，哈希表的键是经过散列函数计算出来的；每一个关键码对应一个值，我们把这种以关键码 -> 值的形式存储数据的数组称为哈希表（散列表）

最简单的哈希函数：把ascll 码加在一起，取模一个数字，最后模出来是多少就是多少（取余数）

class HashTable {
	constructor(){
		// 创建哈希表
		this.table = []; 
	}
	loseHashCode(key){
		let hash = 0 ;
		for(let i=0;i<key.length;i++){
			// 计算KEY unicode码
			hash += key[i].charCodeAt();
		}
		// 取模 37质数，很大程度上避免碰撞
		return hash % 37;
	}
	// 新增元素
	put( key ,value ){
		// 获取key
		const position = this.loseHashCode(key);
		this.table[position] = value;
	}
	// 移除元素
	remove(key){
		this.table[this.loseHashCode(key)] = undefined;
	}
	// 获取元素
	get(key){
		return this.table[this.loseHashCode(key)];
	}
}
const hashtable = new HashTable();
hashtable.put('小白','123@qq.com');
console.log(hashtable);

哈希覆盖

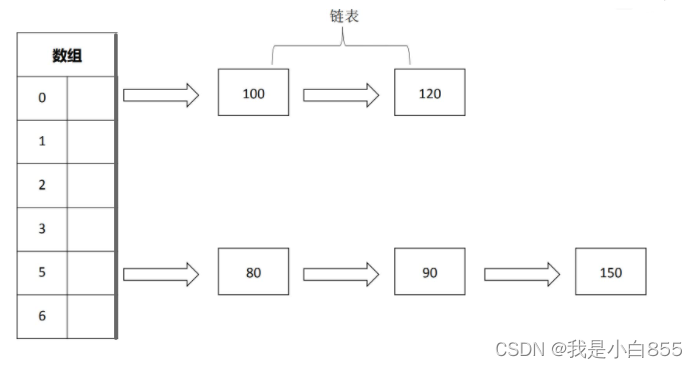
数组里面，下标相同，数据覆盖，哈希表一样，对于不同要存储的数据经过哈希函数的得到的索引有可能相同。

解决方法：

链地址法

开放地址法：

开放地址法是一种解决数据存放冲突的方法，常用的有线性探测、二次探测和再哈希法

线性探测法

寻找空白的位置来放置冲突的数据项

插入的时候,发现原来index位置已经从存储，则从index+1往后找寻空位置，进行插入

查询的时候，查找到空位置就结束，不会查询整个表

删除的时候,不可以设置为NULL。

但是弊端：聚集（一连串填充单元）

当哈希表越来越满时聚集越来越严重，这导致产生非常长的探测长度，后续的数据插入将会非常费时。通常数据超过三分之二满时性能下降严重，因此设计哈希表关键确保不会超过这个数据容量的一半，最多不超过三分之二。

聚集会影响哈希表的性能，无论hi插入、删除、查询

二次探测法

查询优化算法

二次探测是过程是x+1,x+4,x+9，...

二次探测的步数是原始位置相隔的步数的平方

二次探测可以消除在线性探测中产生的聚集问题，但是二次探测还是会产生一种更明确更细的聚集。二次聚集的产生是在二次探测的基础上产生的现象。例如N个数据经hash函数计算后都映射到到数组下标10，探测第二个数字需要以一步长，第三个数字需要以4步长为单位，第四个数字则需要以九为步长。好在二次探测并不常用，解决聚集问题还是有一种更好的办法：再哈希法。