在上期Postgres技术内幕系列直播中,我们为大家介绍了Postgres投影算子和表达式计算实现原理和底层细节。本文根据直播内容整理,作者现任HashData内核研发工程师。
投影 (projection)
关系代数中的一种, 用于从关系R中选出属性包含在A中的列。
在PG中也用于引入额外的列(比如计算表达式)
快问快答
create table t (int a, int b);
以下哪些 sql 会触发投影逻辑?select * from t;select a, b from t;select b, a from t;select a as b, b as a from t;select a from t;select a, b, b from t;select a + 1, b from t;select ctid, * from t;欢迎留言,写下你的答案哦~
PG对投影的实现
整体实现可以分为三个主要部分:
1、判断是否需要投影
当且仅当被扫描的关系的描述符和计划节点的targetlist不匹配的时候,才需要进行投影,tlist_matches_tupdesc 函数用于实现相关的判断逻辑。
static bool
tlist_matches_tupdesc(PlanState *ps, List *tlist, Index varno, TupleDesc tupdesc)
{
int numattrs = tupdesc->natts;
int attrno;
ListCell *tlist_item = list_head(tlist);
/* Check the tlist attributes */
for (attrno = 1; attrno <= numattrs; attrno++)
{
Form_pg_attribute att_tup = TupleDescAttr(tupdesc, attrno - 1);
Var *var;
if (tlist_item == NULL)
return false; /* tlist too short */
var = (Var *) ((TargetEntry *) lfirst(tlist_item))->expr;
if (!var || !IsA(var, Var))
return false; /* tlist item not a Var */
/* if these Asserts fail, planner messed up */
Assert(var->varno == varno);
Assert(var->varlevelsup == 0);
if (var->varattno != attrno)
return false; /* out of order */
if (att_tup->attisdropped)
return false; /* table contains dropped columns */
if (att_tup->atthasmissing)
return false; /* table contains cols with missing values */
/*
* Note: usually the Var's type should match the tupdesc exactly, but
* in situations involving unions of columns that have different
* typmods, the Var may have come from above the union and hence have
* typmod -1. This is a legitimate situation since the Var still
* describes the column, just not as exactly as the tupdesc does. We
* could change the planner to prevent it, but it'd then insert
* projection steps just to convert from specific typmod to typmod -1,
* which is pretty silly.
*/
if (var->vartype != att_tup->atttypid ||
(var->vartypmod != att_tup->atttypmod &&
var->vartypmod != -1))
return false; /* type mismatch */
tlist_item = lnext(tlist, tlist_item);
}
if (tlist_item)
return false; /* tlist too long */
return true;
}
其核心逻辑就是遍历targetlist并判断与扫描表的描述符是否匹配,比较简单,这里不再展开讨论。
2、构建投影所需要的信息
ProjectionInfo *
ExecBuildProjectionInfo(List *targetList,
ExprContext *econtext,
TupleTableSlot *slot,
PlanState *parent,
TupleDesc inputDesc)
{
/* Insert EEOP_*_FETCHSOME steps as needed */
ExecInitExprSlots(state, (Node *) targetList);
/* Now compile each tlist column */
foreach(lc, targetList)
{
/* 考虑投影列为var的情况 */
if (tle->expr != NULL &&
IsA(tle->expr, Var) &&
((Var *) tle->expr)->varattno > 0)
{
if (inputDesc == NULL)
isSafeVar = true; /* can't check, just assume OK */
else if (attnum <= inputDesc->natts)
{
Form_pg_attribute attr = TupleDescAttr(inputDesc, attnum - 1);
/*
* If user attribute is dropped or has a type mismatch, don't
* use ASSIGN_*_VAR. Instead let the normal expression
* machinery handle it (which'll possibly error out).
*/
if (!attr->attisdropped && variable->vartype == attr->atttypid)
{
isSafeVar = true;
}
}
/* 对于简单的情况只需要 EEOP_ASSIGN_*_VAR 即可 */
if (isSafeVar)
{
/* Fast-path: just generate an EEOP_ASSIGN_*_VAR step */
switch (variable->varno)
{
case INNER_VAR:
/* get the tuple from the inner node */
scratch.opcode = EEOP_ASSIGN_INNER_VAR;
break;
case OUTER_VAR:
/* get the tuple from the outer node */
scratch.opcode = EEOP_ASSIGN_OUTER_VAR;
break;
/* INDEX_VAR is handled by default case */
default:
/* get the tuple from the relation being scanned */
scratch.opcode = EEOP_ASSIGN_SCAN_VAR;
break;
}
/*
* 这里是核心逻辑 构建了投影所需要的执行步骤 在执行过程中按照步骤依次执行即可
* 这么做的本质是为了降低函数递归调用的运行成本
*/
ExprEvalPushStep(state, &scratch);
}
else
{
/* 具体来说,包含表达式计算,或者系统变量等情况时,要按照常规方式处理表达式 */
/*
* Otherwise, compile the column expression normally.
*
* We can't tell the expression to evaluate directly into the
* result slot, as the result slot (and the exprstate for that
* matter) can change between executions. We instead evaluate
* into the ExprState's resvalue/resnull and then move.
*/
ExecInitExprRec(tle->expr, state,
&state->resvalue, &state->resnull);
// 投影求值计算的时候会用到 attnum 和 resultnum
scratch.d.assign_var.attnum = attnum - 1;
scratch.d.assign_var.resultnum = tle->resno - 1;
ExprEvalPushStep(state, &scratch);
}
}
}
}
本节我们主要注解了上述代码中 fast-path 相关逻辑,其余逻辑在后续展开讲解。
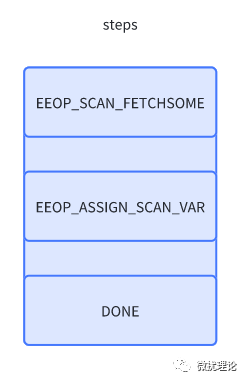
这段代码的核心逻辑在于通过调用 ExprEvalPushStep 构建了用数组表示的投影的执行过程,并通过opcode标识每个步骤的类型,这样在执行阶段即可根据opcode调用不同的过程,请参考下文的执行过程一起理解。
相比于传统的表达式求值逻辑,这样写的好处在于减少函数递归调用。
3、执行投影算子
执行器投影算子入口函数,可以看到关键函数是ExecEvalExprSwitchContext,在PG中和表达式求值有关的逻辑都通过这个函数实现。
#ifndef FRONTEND
static inline TupleTableSlot *
ExecProject(ProjectionInfo *projInfo)
{
ExprState *state = &projInfo->pi_state;
TupleTableSlot *slot = state->resultslot; // 投影之后的结果;目前还是未计算的状态
/* Run the expression, discarding scalar result from the last column. */
(void) ExecEvalExprSwitchContext(state, econtext, &isnull);
return slot;
}
首先要介绍一下PG表达式求值的框架,投影求值也是利用表达式求值实现的,即调用ExecEvalExprSwitchContext ,其底层调用了 ExecInterpExpr。
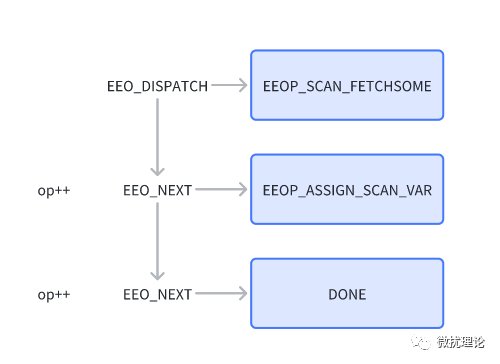
整个执行过程建立在一套由宏定义实现的分发器机制之上,实现了对之前构建的表达式求值步骤顺次执行的逻辑。在过程执行中,我们会用ExprState来存储中间计算结果和其他执行状态。具体代码如下:
// opcode对应步骤的实现逻辑的标识 用于goto
#define EEO_CASE(name) CASE_##name:
// 分发至步骤的执行逻辑
#define EEO_DISPATCH() goto *((void *) op->opcode)
//
#define EEO_OPCODE(opcode) ((intptr_t) dispatch_table[opcode])
// 当前步骤执行完毕时移动至下一个需要执行的步骤
#define EEO_NEXT() \
do { \
op++; \
EEO_DISPATCH(); \
} while (0)
ExecInterpExpr(ExprState *state, ExprContext *econtext, bool *isnull)
{
op = state->steps; // 存储所有的步骤,我们通过宏不断移动当前执行的步骤
resultslot = state->resultslot; // 用于存放最后返回的结果值
innerslot = econtext->ecxt_innertuple;
outerslot = econtext->ecxt_outertuple;
scanslot = econtext->ecxt_scantuple;
EEO_DISPATCH();
EEO_CASE()
EEO_CASE(EEOP_DONE)
{
goto out;
}
EEO_CASE(EEOP_SCAN_FETCHSOME)
{
CheckOpSlotCompatibility(op, scanslot);
slot_getsomeattrs(scanslot, op->d.fetch.last_var);
EEO_NEXT();
}
EEO_CASE(EEOP_ASSIGN_SCAN_VAR)
{
int resultnum = op->d.assign_var.resultnum;
int attnum = op->d.assign_var.attnum;
/*
* We do not need CheckVarSlotCompatibility here; that was taken
* care of at compilation time. But see EEOP_INNER_VAR comments.
*/
resultslot->tts_values[resultnum] = scanslot->tts_values[attnum];
resultslot->tts_isnull[resultnum] = scanslot->tts_isnull[attnum];
EEO_NEXT();
}
out:
*isnull = state->resnull
return state->resvalue
}
这样,我们就实现了投影列计算的逻辑,最终的tuple存储在 state->resultslot里,供上层算子使用。
表达式计算
下面我们介绍表达式计算的实现。表达式计算的过程和前面投影列求值的过程复用了同样的逻辑,即利用同样的分发机制进行求值。
明显不同的地方包括:
1)计算逻辑通常更为复杂,需要多个步骤完成,本质上是以迭代的方式对表达式树进行求值;
2)表达式可以预计算,其中常量的部分在优化器阶段就可以求值,避免迭代过程中重复求值。
下面我们通过一个例子来研究一下表达式树对应的求值步骤时如何构建的。explain select (SQRT(POWER(i,i))) from generate_series(1,5) i;首先,我们看一下PG在内存中是如何表示表达式树的,以上面的查询为例,下述FuncExpr可以非常清晰的找出到(SQRT(POWER(i,i)))的对应关系。
FuncExpr [funcid=1344 funcresulttype=701 funcretset=false funcvariadic=false funcformat=COERCE_EXPLICIT_CALL is_tablefunc=false]
FuncExpr [funcid=1368 funcresulttype=701 funcretset=false funcvariadic=false funcformat=COERCE_EXPLICIT_CALL is_tablefunc=false]
FuncExpr [funcid=316 funcresulttype=701 funcretset=false funcvariadic=false funcformat=COERCE_IMPLICIT_CAST is_tablefunc=false]
Var [varno=1 varattno=1 vartype=23 varnosyn=1 varattnosyn=1]
FuncExpr [funcid=316 funcresulttype=701 funcretset=false funcvariadic=false funcformat=COERCE_IMPLICIT_CAST is_tablefunc=false]
Var [varno=1 varattno=1 vartype=23 varnosyn=1 varattnosyn=1]
一般来说,求解这样的表达式树通常采用递归计算的方式,先算底层表达式,再算高层表达式,整体类似于后序遍历树的过程。
PG为了提高执行效率,选择在执行阶段用投影求值的方式迭代执行,因此在执行初始化阶段需要采用类似于后序遍历树的方式,将每个子表达式加入求值步骤数组中。
构建求值步骤的调用栈如下:
-> ExecBuildProjectionInfo
-> ExecInitExprSlots // EEOP_*_FETCHSOME
->ExprEvalPushStep
for targetList:
-> ExecInitExprRec(tle->expr, )
scratch.resvalue = resv // 当前步骤的结果;上层通过指针传入我们应该存放的地址
case T_FuncExpr:
-> ExecInitFunc // 当前函数 [funcid=1344]
fcinfo = scratch->d.func.finfo
for args: // 这层有一个参数
-> ExecInitExprRec(arg, state, &fcinfo->args[argno].value) // resv - where to stor the result of the node into
case T_FuncExpr:
-> ExecInitFunc // 当前函数 [funcid=1368]
for args: // 这层有两个参数
-> ExecInitExprRec()
case T_FuncExpr:
-> ExecInitFunc // 当前函数 [funcid=316]
for args: // 这层有一个参数 Var [varno=1 varattno=1 vartype=23 varnosyn=1 varattnosyn=1]
-> ExecInitExprRec()
case T_Var:
// regular user column
scratch.d.var.attnum = variable->varattno - 1;
-> ExprEvalPushStep()
ExprEvalPushStep()
ExprEvalPushStep()
ExprEvalPushStep()
ExprEvalPushStep()
scratch.opcode = EEOP_DONE;
ExprEvalPushStep()
整个过程的主体是对表达式树的递归遍历。表达式树通常中间包含若干个 T_FuncExpr或其他类型的表达式节点,每个节点有若干个参数,参数可能同样是一个表达式,子节点求值步骤全部生成后,才将当前步骤生成放入数组;叶子节点通常是 T_Var 或者 T_Const,处理方式和投影一致。
本节重点介绍一下对于 T_FuncExpr 类型的步骤构建过程和之前没讲的非 fast_path 的表达式求值逻辑。主要包含两个函数:ExecInitExprRec 和 ExecInitFunc。
其中 ExecInitExprRec 是表达式求值的关键函数,也是递归调用发生的地方;代码会根据不同的表达式类型,调用不同的逻辑,每个分支根据具体的情况会递归调用 ExecInitExprRec,随后将当前步骤推入步骤数组 ExprEvalPushStep 。其中,有一个很重要的步骤是 scratch.resvalue = resv,这样当前步骤计算完成的值就可以被上层调用者以传指针的方式传入(相当于上层表达式可以拿到子表达式的求值结果),从而将整个递归的计算过程串联起来。
ExecInitFunc 是对函数表达式类型计算的过程,由于比较复杂,写成了一个独立的函数。其主要逻辑是遍历当前函数的参数,分别通过调用ExecInitExprRec进行求值步骤的初始化;子表达式求值的结果则可以通过 &fcinfo->args[argno].value 获取;完成后,将当前函数的求值步骤推入步骤数组。
上述例子的实际求值过程如下,在前述的分发机制中依次执行以下步骤即可:
EEO_CASE(EEOP_SCAN_FETCHSOME)
EEO_CASE(EEOP_SCAN_VAR) // scan i
EEO_CASE(EEOP_FUNCEXPR_STRICT) // i4tod
EEO_CASE(EEOP_SCAN_VAR) // scan i
EEO_CASE(EEOP_FUNCEXPR_STRICT) // i4tod
EEO_CASE(EEOP_FUNCEXPR_STRICT) // dpow
EEO_CASE(EEOP_FUNCEXPR_STRICT) // dsprt
EEO_CASE(EEOP_ASSIGN_TMP) // 将计算结果赋值到resultslot
EEO_CASE(EEOP_DONE)
常量预计算优化
对于表达式树中的常量部分,我们可以在优化阶段就计算好,避免重复求值。同样利用一个例子来讨论这个问题。在下述例子中,如果POWER(2,3)可以在优化阶段即被替换为8,那么在执行阶段,显然就可以避免重复计算5次POWER(2,3)。
select i+POWER(2,3) from generate_series(1,5) i;
调用栈如下:
-> preprocess_expression
-> eval_const_expressions
-> eval_const_expressions_mutator
-> expression_tree_mutator (case T_List)
-> eval_const_expressions_mutator
-> expression_tree_mutator (case T_TargetEntry)
-> eval_const_expressions_mutator (case T_OpExpr)
-> simplify_function
// 对表达式列表递归调用 eval_const_expressions_mutator
-> args = expand_function_arguments()
-> args = (List *) expression_tree_mutator(args,eval_const_expressions_mutator)
-> evaluate_function // try to pre-evaluate a function call
-> evaluate_expr // pre-evaluate a constant expression
// 初始化表达式节点的执行状态信息
-> ExecInitExpr
-> ExecInitExprSlots() // Insert EEOP_*_FETCHSOME steps as needed
-> ExecInitExprRec() // 将执行步骤填入 ExprState->steps 数组
case T_FuncExpr:
-> ExecInitFunc // 主要工作是将 argument 求值;并放入 state 的 list 中
foreach(lc, args)
if IsA(arg, Const)
fcinfo->args[argno].value = con->constvalue
else
ExecInitExprRec() // 递归对表达式参数求值
-> ExprEvalPushStep
-> const_val = ExecEvalExprSwitchContext
-> evalfunc()
op = state->steps
resultslot = state->resultslot
outerslot = econtext->ecxt_outertuple
EEO_DISPATCH() // goto op->opcode
代码的核心逻辑在于通过 eval_const_expressions_mutator 和 express_tree_mutator 函数遍历表达式树;如果遇到 op_expr 则调用 simplify_function()->evaluate_function() 简化子表达树中的常量。evaluate_function 会检查子表达式是否含有非常量;如果全是常量,则可以继续简化。
简化的过程实质就是将执行器阶段的求值过程提前至优化阶段:首先生成节点执行状态信息和求值步骤数组;然后调用 ExecEvalExprSwitchContext 顺次执行;最后通过makeConst生成一个常量节点,替换原来复杂的表达式子节点。
至此,我们就系统地介绍了PG中关于投影和表达式计算的实现逻辑。投影在大部分情况下几乎是一个必须的操作,为数不多的优化手段可能在于将上层算子的投影下推,不再展开讨论。