数字信号处理6

昨天简单的复习了一下离散时间信号是什么以及系统的概念、系统要做的工作和系统中几个简单的原件，今天跟着昨天的内容继续学习。

一、离散时间系统的分类：

为什么要对系统进行分类呢，这就像是我们对函数进行分类一样，有些函数有的性质其他函数没有，相同的，也可能后者有着前者没有的性质，所以，我们要对函数进行分类，同理，系统也一样，一个系统如果有特定的性质，那么这个性质是对所有的输入信号都必须满足，如果说，这个性质只对某些输入信号满足，那他就不具有这个性质，所以，就有了一个常用的判断一个系统是否具有某个性质的方法：举反例，如果举得出来，那这个系统就没有这个性质。

其实，系统的分类方法很多，比如说有：

1、静态-动态系统

2、时不变-时变系统

3、线性-非线性系统

4、因果-非因果系统

5、稳定-不稳定系统

其实，这些在字面意思上就已经很清楚了，但是还是稍微的解释一下：

1、静态：在任意时刻n的输出至多依赖于同一时刻的输入样布，和过去、将来的样本无关，那就是静态或者无记忆的，后面我们会有一种递归的概念，下一时刻和上一时刻是相关的，显然，静态系统没有这个概念

2、动态，那这就很好理解了，动态就是系统n时刻的输出完全由区间n-N到n的输入样本决定，就是说他是有记忆的，那就是个动态系统，而如果我们的N是无穷大，那就说系统是无限记忆。

显然，N=0的情况就是静态系统。

3、时不变、时变：这个更好理解了，系统的输入输出特性不随着时间变化，那就是时不变，相反的，那就是时变系统，就这么理解，我们有个输入信号x(n)，输入到一个系统中，系统的输出是y(n)，假设还有一个和x(n)相同的，但是是提前了k个单位的信号：x(n-k)，系统的输出是y(n-k)，那么我们就可以比较，如果说，y(n-k)和y(n)的特性是相同的，那这个系统他就是时不变的，但如果这两个的特性不一样了，那这个系统就是时变的。

4、线性、非线性：

这两个是很重要的一个分类方法，其他的分类方法在后面的学习中我看到的很少，或者说，几乎没有。

什么是线性呢，书上说的是满足叠加性的系统就是线性系统，或者你就这么理解：有两个输入信号x1、x2和任意常数a，b，那么这两个信号的叠加性就是这样的：

$\tau [ax_1(n)+bx_2(n)]=a\tau[x_1(n)]+b\tau[x_2(n)]$

相应的，对于一个弛豫系统，如果说，零输入却是非零输出，那这个系统就是非线性系统。

5、因果、非因果：

其实这个系统他和静态和动态我感觉差不多，因果不就是依赖于当前和过去的输入么，那他和动态就很像，同样的，非因果它之和当前输入信号有关，和之前的输入信号无关，这和静态就很像。

6、稳定、不稳定：

当然，谁都希望自己的程序是稳定运行的，不是三天两头的出毛病，稳定也是这么个意思，就是系统对信号的处理要非常稳定。

这里我把书上对这两种系统进行一个解答：

一个任意的弛豫系统称为有界输入-有界输出(BIBO)稳定，当且仅当，每个有界输入会产生有限的输出，这就相当于区间极大值和极小值问题也就是说，输入信号之后，系统输出的信号值有上下界，那么这个系统就是稳定的，但如果我们输出的是无界的信号，输出也是无界的信号，那这个系统肯定就是不稳定系统。

二、离散时间系统的相连接：

昨天的最后，我们展示了，加法器、、乘法器（常数、信号）、单位延迟元件、单位超前元件等，他们都有着各自的功能，但是，一个复杂的系统往往需要多个元件组合而成，并不是说，我们用最简单的几个元件就能够实现一个复杂系统的功能，所以这就用到了复杂系统元件的相连接。其实这个没啥好讲的，得具体问题具体分析。

好了，把一些基础性的东西讲完了，现在我们来到了很重要的一部分：线性时不变系统(LTI)

一、线性系统的分析：

对于给定的信号，系统的输出这么分析呢，主要有这么两种办法：

1、基于系统输入输出方法的直接求解，

2、输入信号分解，分别处理后再将响应相加。

LTI系统输入输出关系的一般形式是：

$y(n)=-\sum_{k=1}^N a_ky(n-1)+\sum_{k=0}^Mb_kx(n-k)$

这个后面的差分方程求解中会用到。

第二种的话，就是我们把一个输入信号x(n)给他分解成多个基本信号成分的加权和：

$x(n)=\sum_kc_kx_k(n)$

当我们对每个信号用系统进行处理之后，再加起来就成了输入是x(n)的输出。

有个很简单的方法，如果说，我们对输入信号的特性并没有做限制，那就把输入信号分解成单位冲激序列的加权和，这样是比较方便的。

那么，怎么样才能把输入信号分解成单位冲激序列的加权和呢，我们得先求解系统对单位采样序列的响应，然后用线性系统的特性来求解对于给定输入信号的输出公式：

那么我们对于一个输入信号x(n)：

选取基本的信号：

$x_k(n)=\delta(n-k)$

其中，

$\delta(n-k)=\left\{\begin{matrix} 1 ,n=k\\ 0,n\neq k \end{matrix}\right.$

这样的话，将两者相乘： $x(n)\delta(n-k)=x(k)\delta(n-k)$ ，这样我们就构成了一个只在n=k处值为x(k)以外，其他值都是0的序列，同理的，我们就可以构建多个只在特定位置（如n=k）处有值而其他位置均为0的序列，那么显而易见，我们就通过这个方法实现了对一个线性系统的划分：

$x(n)=\sum_{k=-\infty}^{\infty}x(k)\delta(n-k)$

我用一个矩阵的形式来表示一下，就是，假设我们有个线性系统，输入信号是 $x(n)=\left\{1,2,3,2,1\right\}$ ,用上述方法给拆分成单位冲激响应之后，就有了如下形式：

$\begin{bmatrix} 1 &0 & 0 & 0 &0 \\ 0& 2 & 0 & 0 &0 \\ 0& 0 &3 & 0 &0 \\ 0& 0& 0&2 &0 \\ 0& 0& 0& 0 &1 \end{bmatrix}$

这其中，每一行都是一个进行了加权的单位冲激序列，当然，我这就是简单的一写，书上有个更加好的例子，我给稍微改了一下：

有一个有限长序列：

$x(n)=\left\{5,2,\underset{\perp }4,0,1,3\right\}$

我们看到，在这个序列中，-2，-1，0，2，3这五个数值非零，也就是说，在-2，-1，0，1，3这五个时刻的值是非0的，所以，我们就需要在k=这5个时刻的冲激，最后得到的x(n)就是这样子的：

$x(n)=5\delta(n+2)+2\delta(n+1)+4\delta(n)+\delta(n-2)+3\delta(n-3)$

其实我更喜欢上面那个用矩阵表示的，因为我觉得那个好看一些。

二、LTI对任意输入的响应的计算：

这里，，就要说到今日最重要的一个内容：卷积和

我们用LTI系统对输入信号x(n)和单位采样冲激h(n)来给出LTI的响应:y(n):

$y(n)=\sum_{k=-\infty}^{\infty} x(k)h(n_0-k)$

说法就是输入x(n)和冲激响应h(n)的卷积产生输出y(n)。

那么，卷积怎么计算呢？这才是今天的重点内容，但是其实也简单，四个步骤：反转、移位，乘积、求和，直接看图最简单了：

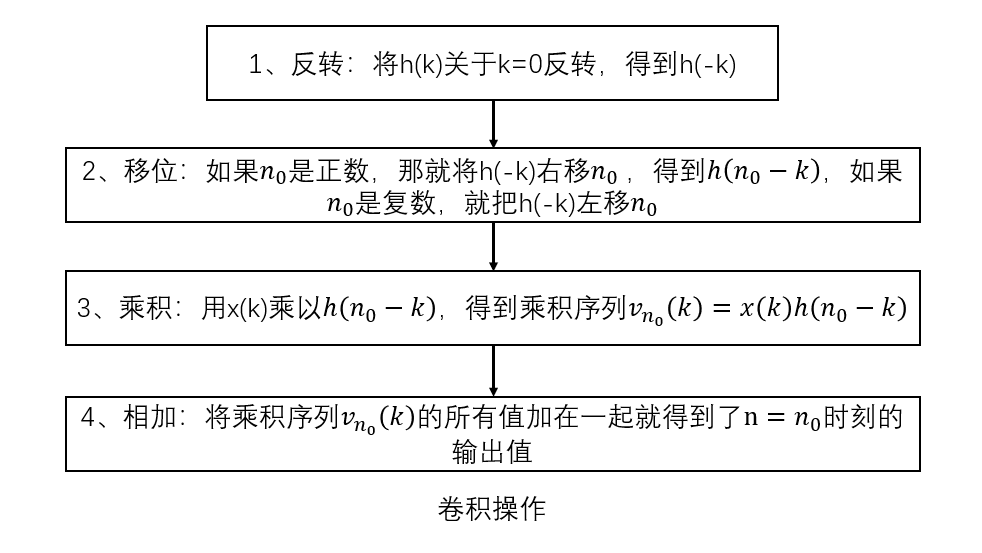
就用书上的例子吧：

$h(n)=\left\{1,\underset{\wedge }2,1,-1\right\}$ , $x(n)=\left\{\underset{\wedge }1,2,3,1\right\}$

让我们来计算：

1、反转：我们把h给反转了：

$h(k)=\left\{1,\underset{\wedge }2,1,-1\right\}-> h(-k)=\left\{-1,1,\underset{\wedge }2,1\right\}$

2、移位、乘积：

n=0的时候，响应序列：

$v_0(k)=x(k)h(-k)$

依次计算n=-1,1,2,3,4,5的响应序列：

$v_{-1}(k) ,v_{1}(k), v_{2}(k), v_{3}(k), v_{4}(k), v_{5}(k)$

3、求和：把上述的响应序列全给加起来，我们就得到了LTI系统的计算结果。

后面还会学到一种和卷积很相似的运算，但是两者的意义是不一样的，不能把两者给搞混淆了。

其实，上次听课的时候我就以及了解了卷积的一个知识，但是我还没有学到那里，所以一直在纠结到底写不写他，但是，想了想，时频现在都在用，写写无妨：时域的卷积是想加形式，频率域的卷积是相乘形式，这两者通过转化，实际上是一样的效果。我想简单的写一下卷积，emm，试试看呗，能写出来更好，写不出来的话，numpy也提供了卷积操作np.convolve(x,h)直接用也行。

import numpy as np
x=np.array([1,2,1,-1])
#单位冲激响应
h=np.array([1,2,3,1])
y=np.zeros(len(x)+len(h)-1,dtype=int)
for i in range(len(x)):
    for j in range(len(h)):
        y[i+j]+=x[i]*h[j]
print(y)
print(np.convolve(x,h))

结果是一样的，这我就放心了。

然后，我找了个图，我觉得这个对算法的讲解比较好：

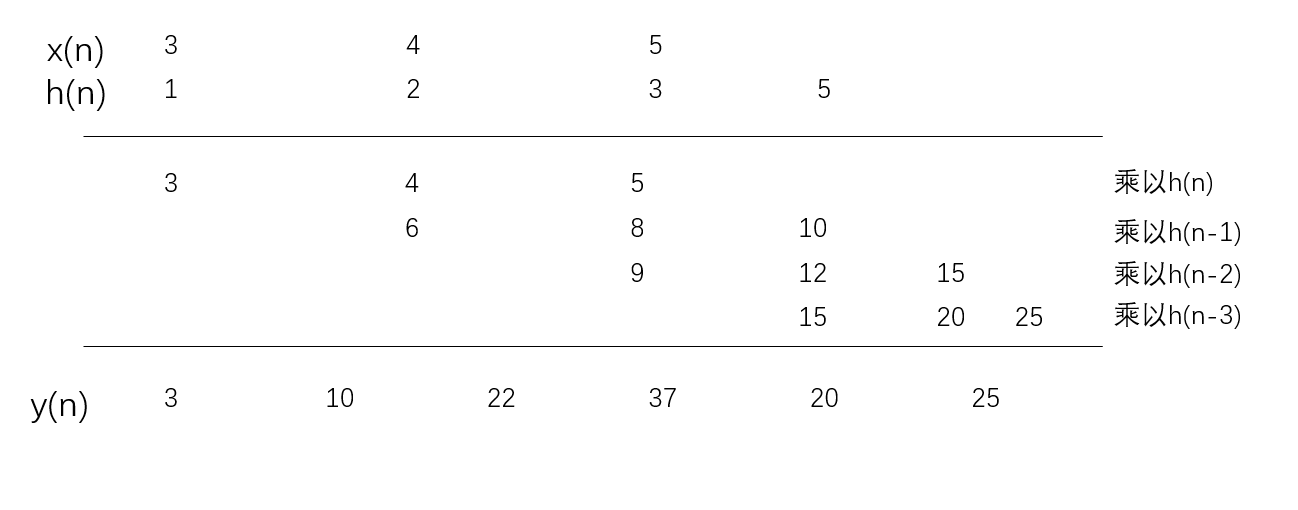
其实，从这个算法看出来的就是，对h每次提前一个单位。

后面呢这个就可以更好的解释了：

这两个方法其实是等价的：

$\left\{\begin{matrix} y(n)=\sum_{k=-\infty}^\infty x(k)h(n-k)\\ \\ y(n)=\sum_{k=-\infty}^\infty x(n-k)h(k) \end{matrix}\right.$

上面的图和我的代码就是用的第一种情况，在实际计算机中会方便很多，要是你用手算的话，那就1-4步老老实实的去计算。

好了，卷积的计算就说完了，但是卷积有哪些性质呢？

1、恒等性、位移性：

当我们采用单位采样序列的时候，我们的卷积是这个样子滴：

$x(n)\delta(n-k)=y(n-k)=x(n-k)$

神奇吧，就相当于提前了k个单位

2、交换律、结合律、分配：

和数学中的交换结合类似，就是符号变了变，之后，我们在使用卷积的时候，通常用的是*：

交换：

$x(n)*h(n)=h(n)*x(n)$

结合：

$y(n)=[x(n)*h(n)]*h_2(n)=x(n)*[h(n)*h_2(n)]$

分配：

$y(n)=x(n)*[h_1(n)+h_2(n)]=x(n)*h_1(n)+x(n)*h_2(n)$

从结合律可以得到一个很有意思的性质：如果我们有L个冲激响应为 $h_1(n),h_2(n),\cdots,h_L(n)$ 的线性时不变系统级联在一起，那么就有一个等价的LTI系统，其冲激响应等于这些冲激响应的L-1重卷积：

$h(n)=h_1(n)*h_2(n)*\cdots*h_L(n)$

同样的，我们也可以把这个性质给反转过来，一个LTI系统必然可以分解成为级联的子系统。

相似的，从分配率中也可以得到的一个性质：多个冲激响应的组合可以成为一个大的冲激响应，而一个大的冲激响应是可以转换成若干个小的冲激响应的。

因果LTI系统：

之前我们就讲解了因果系统，这是一个什么样子的系统呢？同一片博客，应该是有印象的，因果系统就是某一时刻的输出依赖之前的输出， $n=n_0$ 时刻的输出依赖的是 $n\leqslant n_0$ 时刻的信号。

emm，就用书上给的例子吧，我也想不出来啥好的自己举例：

有这么一个LTI系统，我们知道其在 $n=n_0$ 时刻的输出：

$y(n_0)=\sum_{k=-\infty}^{\infty}h(k)x(n_0-k)$

然后，我们把这个输出转换成两组，一组包含当前和过去的值，另一组则包含将来的值：

$y(n_0)=\sum_{k=-\infty}^{\infty}h(k)x(n_0-k)=\sum_{k=0}^{\infty}h(k)x(n_0-k)+\sum_{k=-\infty}^{-1}h(k)x(n_0-k)=[h(0)x(n_0)+h(1)h(n_0-1)+\cdots]+[h(-1)x(n_0+1)+h(-2)h(n_0+2)+\cdots]$