2022年华数杯全国大学生数学建模
A题 环形振荡器的优化设计
原题再现:
芯片是指内含集成电路的硅片,在我们日常生活中的手机、电脑、电视、家用电器等领域都会使用到,是高端制造业的核心基石。芯片的制造工艺非常复杂,要经历上千道工序经过复杂工艺加工制造。尤其是数字芯片,随着工艺尺寸的不断缩小,数字芯片的优化设计变得尤为重要。
而环形振荡器是数字时钟芯片中的一种重要的结构,其设计中有三个重要的指标需要考虑:速度、面积和功耗。速度是指电路运行的时钟频率,一般来说,速度越快,能处理的数据量就越多,性能越好。面积是指电路的物理实现需要占用硅片的面积,占用的面积越小,芯片成本越低。功耗是指电路工作所消耗的能量,功耗越低,发热量也越低,设备工作的时间更长,使用寿命越久。速度、面积、功耗是互相牵制的,在相同的制造工艺(制程)以及相同的电路条件下,一般来说,速度越快,晶体管尺寸越小,功耗也越高,反之亦然。相关概念与参数介绍见附录 1。
请阅读相关文档说明,回答下列问题。


整体求解过程概述(摘要)
本文针对环形振荡器的优化设计和多项目晶圆布图规划进行了研究。首先建立了环形振荡器的输出频率计算模型,并求解了不同参数环形振荡器的输出频率,然后基于此模型建立了在给定输出频率和反相器个数情况下,环形振荡器面积最小的优化模型和在给定输出频率条件下,环形振荡器功耗最小的优化模型,并分别用二分法和遗传算法求解了模型。最后建立了多项目晶圆布图规划剩余矩形面积最大的优化模型,并利用模拟退火算法求解了模型。计算了晶圆上最多可安放环形振荡器的数目。
针对问题一,建立了环形振荡器的输出频率计算模型,并求解了不同参数的环形振荡器的输出频率。首先分别求出了在不同阶段反向器的工作电流和其负载电容的值,然后再计算出反向器的下降沿延迟时间和上升沿延迟时间,得到反向器的平均延迟时间,最后利用环形振荡器中反向器的个数求得环形振荡器的输出频率。将求解结果记录在表格中。
针对问题二,建立了环形振荡器输出频率误差最小的优化模型,并用二分法求解模型得到了最
优决策变量。首先分析第一问模型得到输出频率与栅宽无关且与栅长有单调关系,因此将栅长作为决策变量,栅长宽范围作为约束条件,输出频率误差最小作为优化目标建立优化模型。再利用二分法求解出栅长的最优解。最后解出栅长值取 63.6967nm,栅宽值都取 120.0000nm。环形振荡器的最小面积为 7.0147um2。
针对问题三,建立了环形振荡器功耗最小的单目标多决策变量优化模型,并借助遗传算法求解了模型。首先将栅长宽范围和环形振荡器输出频率为 5MHZ 作为约束条件,晶体管的栅长宽和反向器个数作为决策变量,环形振荡器的动态功耗最小作为目标函数建立优化模型。再利用遗传算法,将环形振荡器动态功耗最为适应度函数,解出最优决策变量即:反相器的个数为 3 个,栅长值取370.8873nm,栅宽值都取 120.0000nm。环形振荡器的最小功率为 6.0314uW。
针对问题四,建立了多项目晶圆布图规划剩余矩形面积最大的优化模型,并借助模拟退火算法求解了模型。首先用横向编码描述了模块间的拓扑结构,以模块的位置和方向作为决策变量建立剩余矩形面积最大的优化模型。然后借助模拟退火算法,将剩余矩形面积的相反数和超过晶圆的面积作为损失函数,基于 Metropolis 准则求解模型。最后再经过人工干预得到最优的布图方案。得出剩余最大矩形的长为 2420um,宽为 534um,矩形的面积为 1.2923mm2。基于第三问模型求解出环形振荡器尺寸最优解为:长 56.85um,宽为 0.31um。因此第七个芯片上最多可放下 73278 个环形振荡器。
本文模型的优点为:1.抓住了问题的主要矛盾,对晶体管在不同工作区进行了分类,模型贴合实际。2.进行了合理的假设,在优化模型中抓住了核心的决策变量,让模型和算法简单高效。3.在布图规划中用横向编码描述了模块间的拓扑结构,简单且更利于算法实现,用模拟退火算法等启发式算法进行了全局搜索,得到的优化结果具有一定的参考意义。
模型假设:
1. 假设反相器输出的高电平为电源电压, 反相器输出的低电平电压为电源电压的五十分之一。
2. 假设在环形振荡器中, 下一级反相器在上一级反相器输出稳定后才开始变化。
3. 假设对环形振荡器电路功耗起支配作用的是由充电放电引起的动态功耗。
问题分析:
问题一分析
本问给出了不同环形振荡器的参数, 要求确定每个环形振荡器的输出频率。首先, 分不同晶体管, 不同工作阶段计算单个反相器对负载电容的充放电时间, 然后再算出反相器上升沿和下降沿时间, 最后平均得到反向器的延迟时间, 再结合反向器的个数求得输出频率。将本问给出的参数带入模型中可求出环形振荡器输出频率。
问题二分析
本问给出环形振荡器的输出频率和反相器个数, 要求确定环形振荡器面积最小时的晶体管尺寸。首先分析第一问的模型可知输出频率和栅极宽无关, 若要环形振荡器面积最小栅宽应当取极小值。因此建立以栅长为决策变量, 输出频率误差最小的优化模型, 用二分法求解模型得到栅长的最优解, 当栅宽取最小值时可求出环形振荡器的最小面积。
问题三分析
本问给出了环形振荡器的输出频率, 要求确定环形振荡器功耗最小时反相器的个数和晶体管的尺寸。首先, 将环形振荡器的动态功耗最小作为目标函数, 栅长宽范围和环形振荡器输出频率为 5MHZ 作为约束条件, 晶体管的栅长宽和反向器个数作为决策变量建立单目标多决策变量优化模型。然后将动态功耗作为适应度函数, 利用遗传算法求解出最优的决策变量。最后将最优决策变量带入目标函数可求出环形振荡器最小功耗。
问题四分析
本问给出了芯片在流片时晶圆的总面积和晶圆上其他 6 块芯片的尺寸, 要求确定在环形振荡器的功耗最小时, 输出频率为 2KHz 的环形振荡器的尺寸并确定多项目晶圆的布图方式, 以达到在晶圆上安装更多环形振荡器的目的。首先本问用横向编码描述了模块间的拓扑结构, 方便算法的实现。然后以模块的位置和方向作为决策变量建立剩余矩形面积最大的优化模型, 再借助模拟退火算法求解出了横向编码所能确定的最优布图方式, 最后人工干预得到了最优的布图方案。同时基于第三问的模型求出了环形振荡器的尺寸, 结合最优布图方案确定了可安放环形振荡器的数量。
模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:(代码和文档not free)
论文及程序仅供学习与参考
function f = Cacuf(W,L,n) %输入参数单位为m
V_limited = 0.024;
K_r = 68.7134 .* 1e-6;
K_f = 111.6634 .* 1e-6;
Vgs = 1.2;
time_foot = 1e-10; %时间步长1e-10
Vth_r = 0.398;
Vth_f = 0.42;
Vds = V_limited;
C = 3.137 * L * W;
time_rise = 0;
time_fall = 0;
%% rise
k1 = Vgs - Vth_r;
while 1
if Vds < k1
Id = K_r .* (W ./ L) .* ( k1 .* Vds - Vds .* Vds ./2);
else
Id = 1 ./ 2 .* K_r .* (W ./ L) .* k1 .* k1;
end
Vds = Vds + Id .* time_foot ./ C;
time_rise = time_rise + 1;
if Vds >= Vgs
break;
end
end
%% fall
k2 = Vgs - Vth_f;
while 1
if Vds < k2
Id = K_f .* (W ./ L) .* (k2 .* Vds - Vds .* Vds ./2);
else
Id = 1 ./ 2 .* K_f .* (W ./ L) .* k2 .* k2;
end
Vds = Vds - Id .* time_foot ./ C;
time_fall = time_fall + 1;
if Vds <= V_limited
break;
end
end
%%
tpd = ( time_rise + time_fall) ./2 .* time_foot;
f = 1 ./ ( 2 .* n .* tpd);
K_r = 68.7134 .* 1e-6;
K_f = 111.6634 .* 1e-6;
lastdw = 1e-9;
f = zeros(10,1);
Vth_r = 0.398;
Vth_f = 0.42;
Vgs = 1.2;
V_limited = 0.024;
time_foot = 1e-15; %时间步长1e-10
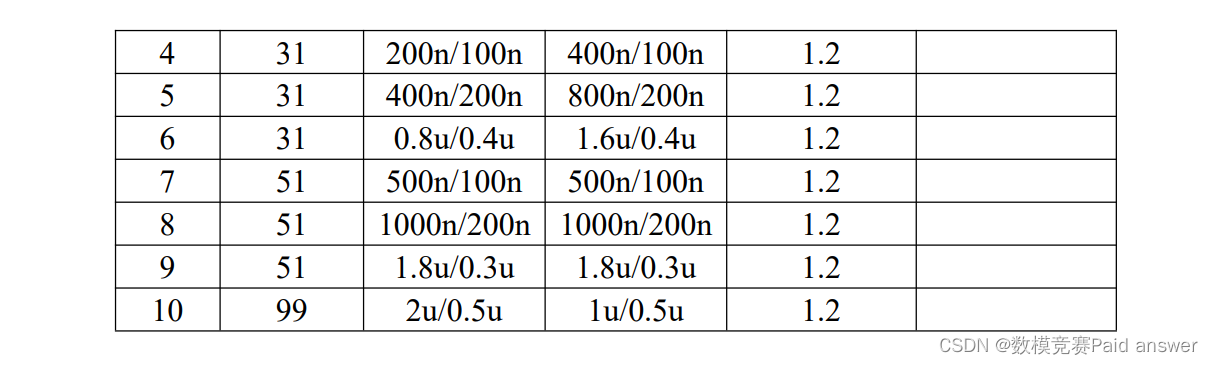
W_each = [[400 200];[800 400];[1600 800];[200 400];[400 800];[800 1600];[500 500];[1000
1000];[1800 1800];[2000 1000]];
L_each = [100 200 400 100 200 400 100 200 300 500];
n_each = [11 11 11 31 31 31 51 51 51 99];
for i = 1:10
W = (W_each(i,1) + W_each(i,2)) .* lastdw;
L = L_each(i) .* lastdw;
C = 3.137 * L * W;
Vds = V_limited;
n = n_each(i);
f(i) = Cacuf(W,L,n);
end