本文已收录于专栏 《算法合集》

---

---

一、简单释义

1、算法概念

  堆排序（Heap Sort）是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

2、算法目的

  把无序数组通过转换成堆的形式，通过堆的各个结点比较进行交换位置，最后形成一个有序数组  (文中以大根堆为例)

3、算法思想

  将待排序的序列构造成一个大根堆 或小根堆(文中以大根堆为例)，然后将堆顶元素与最后一个元素交换位置 ，再将剩余元素重新构造成一个堆，重复执行以上操作，直到整个序列有序。

4、算法性质

以大根堆为例，它总是满足下列性质：

  1. 空堆是一个大根堆
  2. 大根堆中某个结点的关键字小于等于其父结点的关键字；
  3. 大根堆是一个完全二叉树

二、核心思想

构建

  构造堆的过程就是将无序的序列构造成一个堆的过程。

排序

  将堆顶元素与最后一个元素交换位置，然后将剩余元素重新构造成一个堆的过程。

三、图形展示

宏观展示

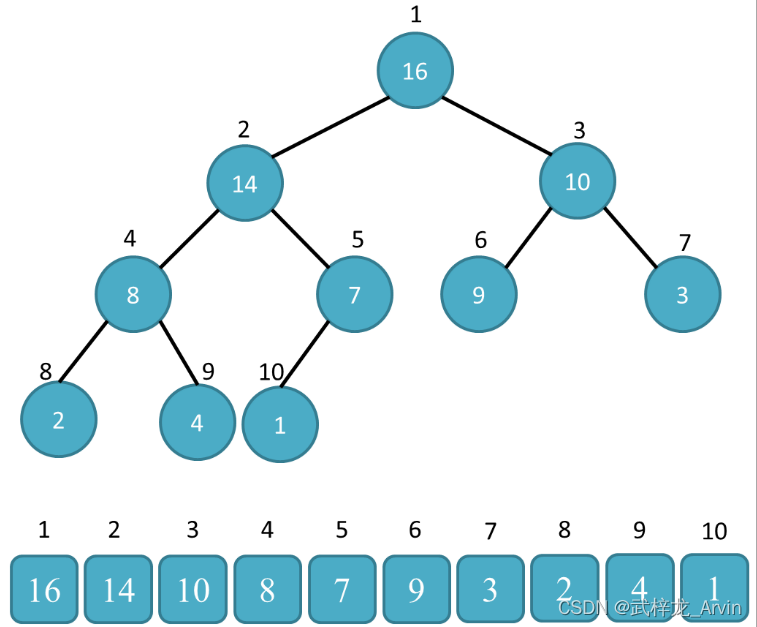
微观展示

  以4、6、3、5、9这个数组为例，根据数组构建二叉堆。

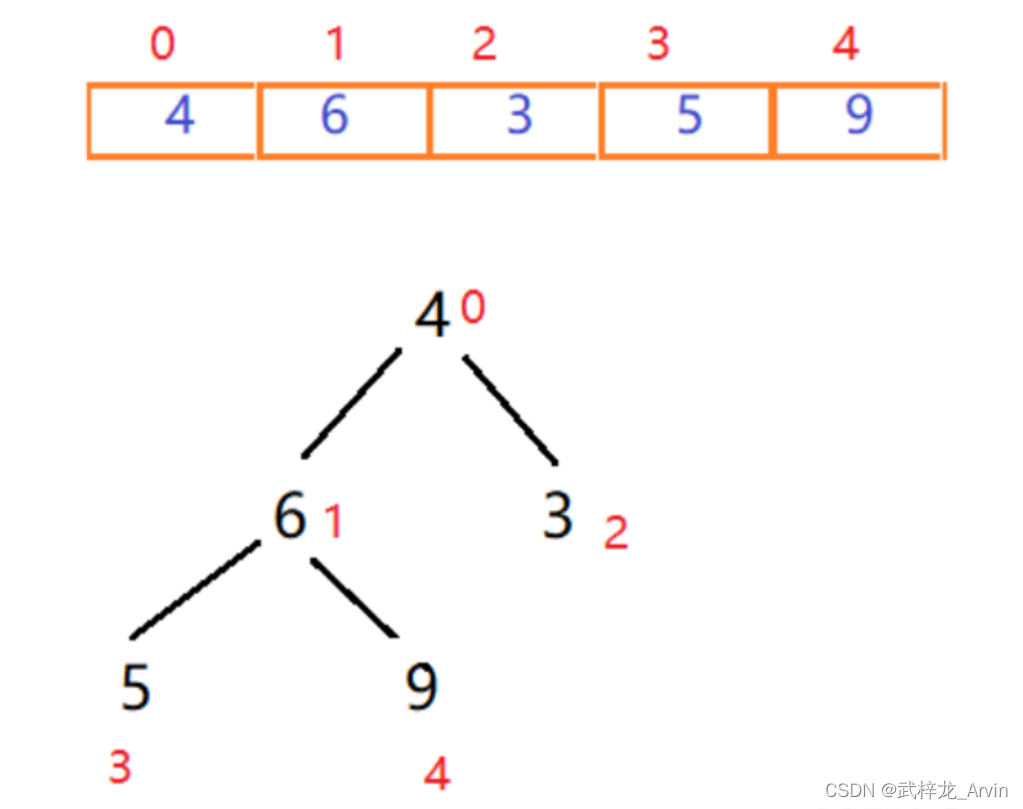
  1、第一次排序：从叶子结点往上进行比较，首先是5和6比较，5小于6不交换位置。然后9和6进行比较，9大于6交换位置。

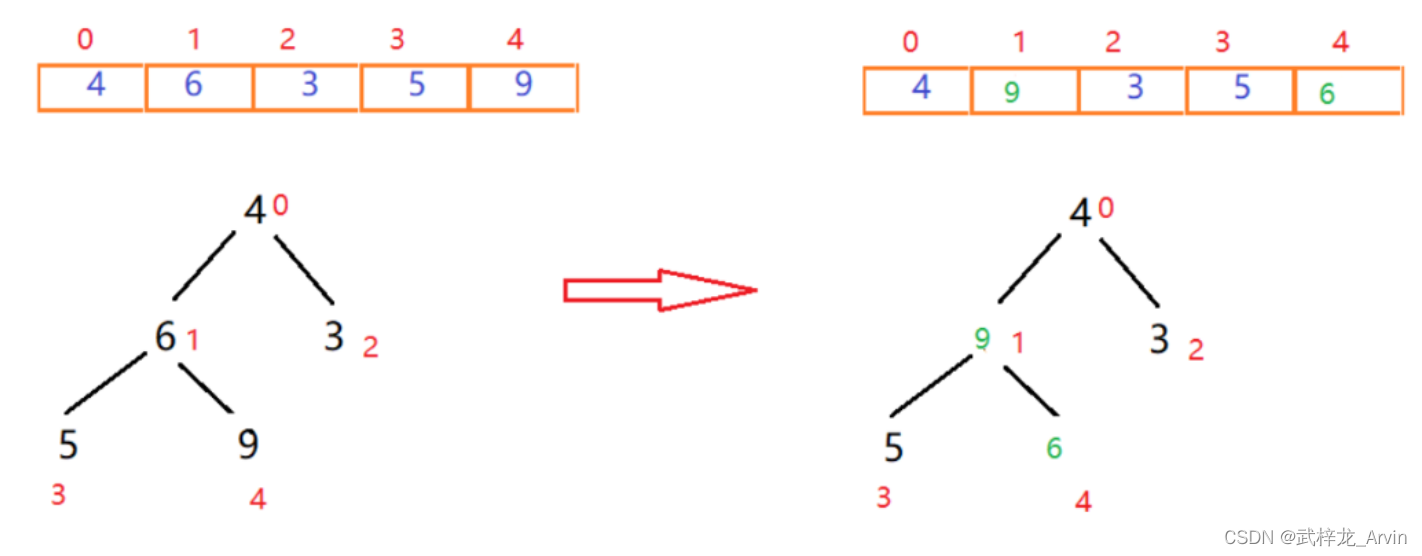
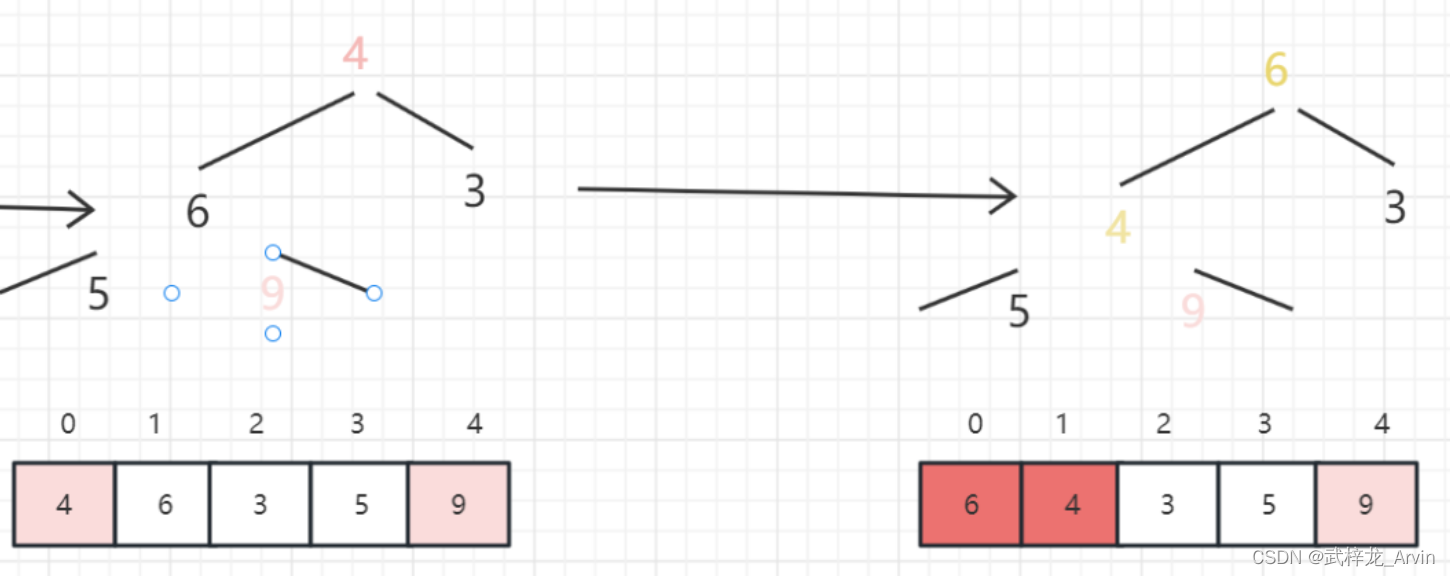
  2、第二次排序：9和4进行对比，9大于4交换位置。然后6和4进行比较，6大于4交换位置。最终的到一个最大值9。9和4交换位置继续排序。

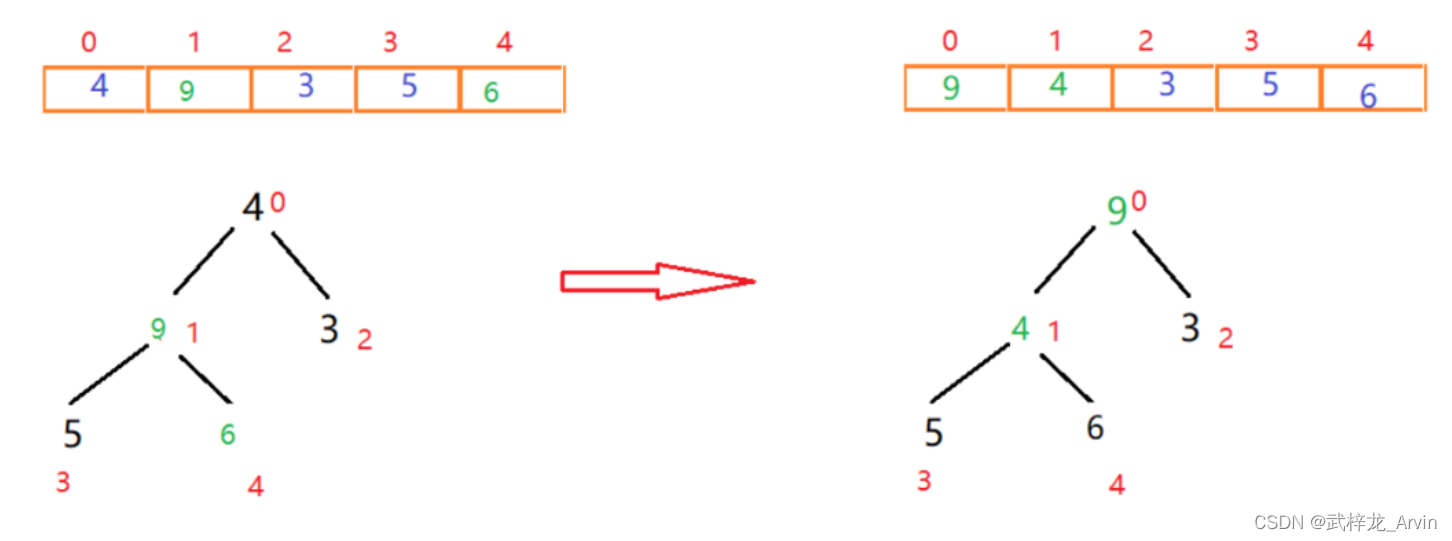
  3、第三次排序：重复上述操作。

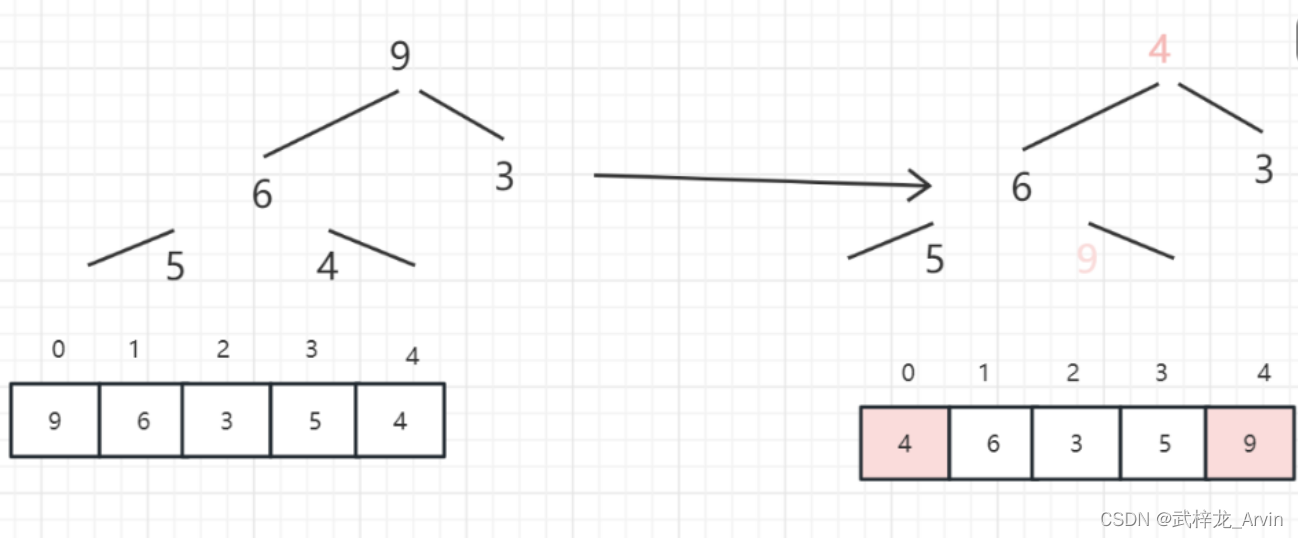
  4、第四次排序

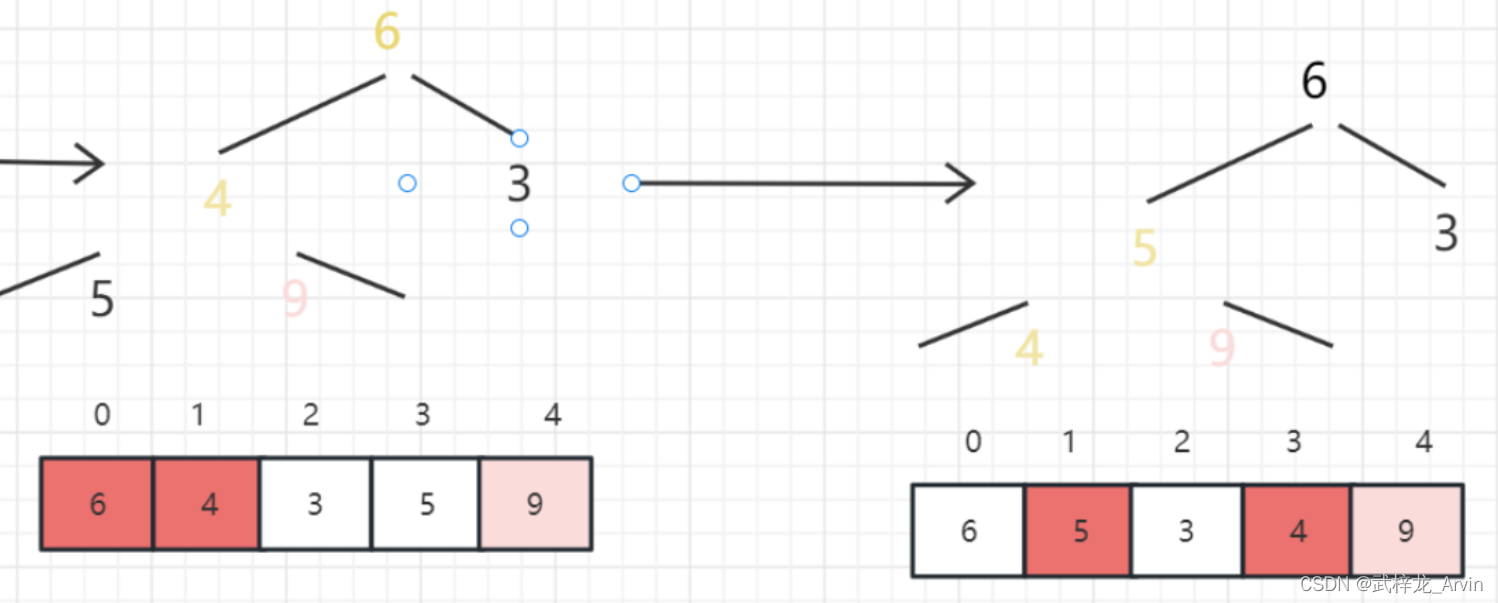
  5、第五次排序

四、算法实现

实现思路

  将图形化展示的过程转换成对应的开发语言，本文中主要以Java语言为例来进行算法的实现。

  1、首先将待排序的数组构造成一个大根堆，此时，整个数组的最大值就是堆结构的顶端
  2、将顶端的数与末尾的数交换，此时，末尾的数为最大值，剩余待排序数组个数为n-1
  3、将剩余的n-1个数再构造成大根堆，再将顶端数与n-1位置的数交换，反复执行，便能得到有序数组

  能把整个过程描述清楚实现起来才会更加容易！！！

代码实现

客户端调用

/**
 * @BelongsProject: demo
 * @BelongsPackage: com.wzl.Algorithm.HeapSort
 * @Author: Wuzilong
 * @Description: 堆排序
 * @CreateTime: 2023-05-22 11:45
 * @Version: 1.0
 */

public class HeapSort {

    public static void main(String[] args) {
        int[] numArray={4,6,3,5,9};
        heapSort(numArray);

    }
}

构造堆的方法

	//构造堆的方法
    public static void heapSort(int[] arr) {
        int n = arr.length;

        // 构造大根堆
        for (int i = n / 2 - 1; i >= 0; i--) {
            heapify(arr, n, i);
        }

        // 交换堆顶元素和最后一个元素，并重新构造堆
        for (int i = n - 1; i >= 0; i--) {
            swap(arr, 0, i);
            heapify(arr, i, 0);
            System.out.println( Arrays.toString(arr));
        }
    }

元素交换的方法

    private static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

元素比较的方法

    private static void heapify(int[] arr, int n, int i) {
        int largest = i;
        int left = 2 * i + 1;
        int right = 2 * i + 2;

        if (left < n && arr[left] > arr[largest]) {
            largest = left;
        }
        if (right < n && arr[right] > arr[largest]) {
            largest = right;
        }
        if (largest != i) {
            swap(arr, i, largest);
            heapify(arr, n, largest);
        }

    }

运行结果

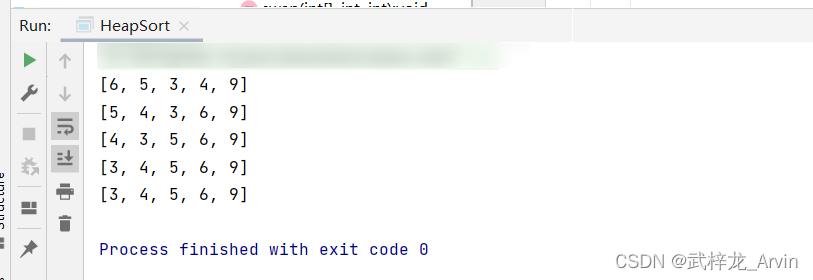
五、算法描述

1、问题描述

  通过给定的数据集合，创建堆。可以先创建堆数组的内存空间。然后一个一个执行堆的插入操作。

2、算法过程

整个算法过程分为以下几步：
  1）将待排序序列构造成一个大根堆或小根堆。
  2）将堆顶元素与最后一个元素交换位置，堆的大小减一。
  3）对剩余元素重新构造成一个堆。
  4）重复执行步骤 2 和步骤 3，直到整个序列有序。

3、算法总结

  构造的过程就是将无序的序列构造成一个堆的过程。堆的定义是：对于任意一个非叶子节点 i，其左子节点为 2i+1，右子节点为 2i+2，且父节点的值大于等于（或小于等于）其子节点的值。因此，我们可以从最后一个非叶子节点开始，依次将其与其子节点比较，如果不满足堆的定义，则交换位置，直到整个序列构造成一个堆为止。
  排序的过程就是将堆顶元素与最后一个元素交换位置，然后将剩余元素重新构造成一个堆的过程。每次交换后，堆的大小减一，因此我们可以通过一个变量来记录堆的大小，从而将排序的过程限制在堆的范围内。

六、算法分析

1、时间复杂度

  堆排序是一种基于二叉堆的排序算法，其时间复杂度：最好、最坏和平均均为 O(nlogn)

2、空间复杂度

  堆排序是一种原地排序算法，所以空间复杂度为 O(1)。

3、算法稳定性

  堆排序是一种不稳定的排序算法。在堆排序过程中，由于交换堆顶元素和最后一个元素的位置可能会改变相同元素之间的相对顺序，所以堆排序不是稳定的排序算法。

🎯 此文章对你有用的话记得留言+点赞+收藏哦🎯