【深度学习入门到进阶】必看系列,含激活函数、优化策略、损失函数、模型调优、归一化算法、卷积模型、序列模型、预训练模型、对抗神经网络等

专栏详细介绍:【深度学习入门到进阶】必看系列,含激活函数、优化策略、损失函数、模型调优、归一化算法、卷积模型、序列模型、预训练模型、对抗神经网络等
本专栏主要方便入门同学快速掌握相关知识。声明:部分项目为网络经典项目方便大家快速学习,后续会不断增添实战环节(比赛、论文、现实应用等)
专栏订阅:深度学习入门到进阶专栏
卷积算子:空洞卷积、分组卷积、可分离卷积、可变性卷积等详细讲解以及应用场景和应用实例剖析
1.空洞卷积(Dilated Convolution)
1.1 空洞卷积提出背景
在像素级预测问题中(比如语义分割,这里以FCN[1]为例进行说明),图像输入到网络中,FCN先如同传统的CNN网络一样对图像做卷积以及池化计算,降低特征图尺寸的同时增大感受野。但是由于图像分割是一种像素级的预测问题,因此我们使用转置卷积(Transpose Convolution)进行上采样使得输出图像的尺寸与原始的输入图像保持一致。综上,在这种像素级预测问题中,就有两个关键步骤:首先是使用卷积或者池化操作减小图像尺寸,增大感受野;其次是使用上采样扩大图像尺寸。但是,使用卷积或者池化操作进行下采样会导致一个非常严重的问题:图像细节信息被丢失,小物体信息将无法被重建(假设有4个步长为2的池化层,则任何小于 2 4 2^4 24pixel 的物体信息将理论上无法重建)。
1.2 空洞卷积及其应用
空洞卷积(Dilated Convolution),在某些文献中也被称为扩张卷积(Atrous Deconvolution),是针对图像语义分割问题中下采样带来的图像分辨率降低、信息丢失问题而提出的一种新的卷积思路。空洞卷积通过引入扩张率(Dilation Rate)这一参数使得同样尺寸的卷积核获得更大的感受野。相应地,也可以使得在相同感受野大小的前提下,空洞卷积比普通卷积的参数量更少。
空洞卷积在某些特定的领域有着非常广泛的应用,比如:
-
语义分割领域:DeepLab系列[2,3,4,5]与DUC[6]。在DeepLab v3算法中,将ResNet最后几个block替换为空洞卷积,使得输出尺寸变大了很多。在没有增大运算量的前提下,维持分辨率不降低,获得了更密集的特征响应,从而使得还原到原图时细节更好。
-
目标检测领域:RFBNet[7]。在RFBNet算法中,利用空洞卷积来模拟pRF在人类视觉皮层中的离心率的影响,设计了RFB模块,从而增强轻量级CNN网络的效果。提出基于RFB网络的检测器,通过用RFB替换SSD的顶部卷积层,带来了显著的性能增益,同时仍然保持受控的计算成本。
-
语音合成领域:WaveNet[8]等算法。
1.3 空洞卷积与标准卷积的区别
对于一个尺寸为 3 × 3 3\times{3} 3×3 的标准卷积,卷积核大小为 3 × 3 3\times{3} 3×3 ,卷积核上共包含9个参数,在卷积计算时,卷积核中的元素会与输入矩阵上对应位置的元素进行逐像素的乘积并求和。而空洞卷积与标准卷积相比,多了扩张率这一个参数,扩张率控制了卷积核中相邻元素间的距离,扩张率的改变可以控制卷积核感受野的大小。尺寸为 3 × 3 3\times{3} 3×3 ,扩张率分别为 1 , 2 , 4 1,2,4 1,2,4 时的空洞卷积分别如 图1,图2,图3所示。
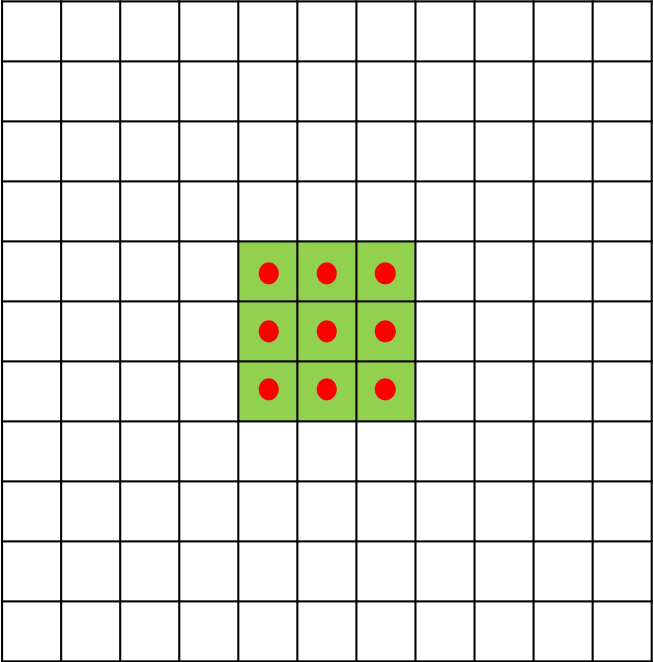
图1 扩张率为1时的3*3空洞卷积
扩张率为1时,空洞卷积与标准卷积计算方式一样。
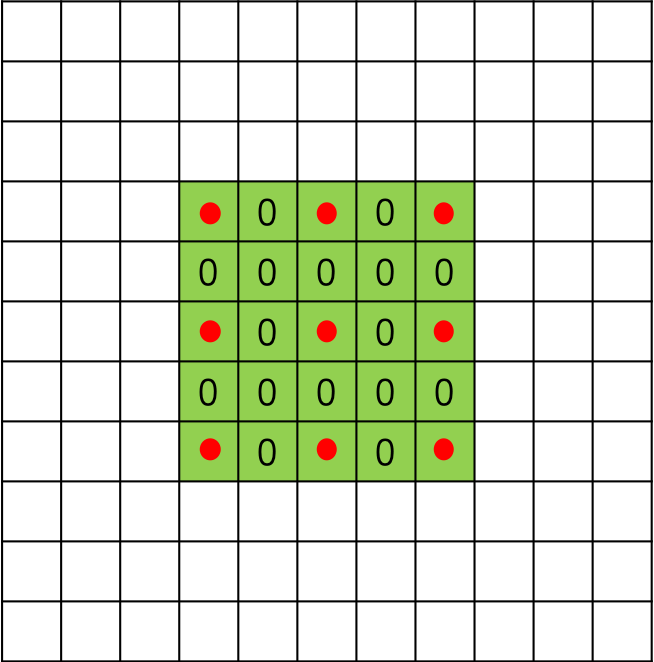
图2 扩张率为2时的3*3空洞卷积
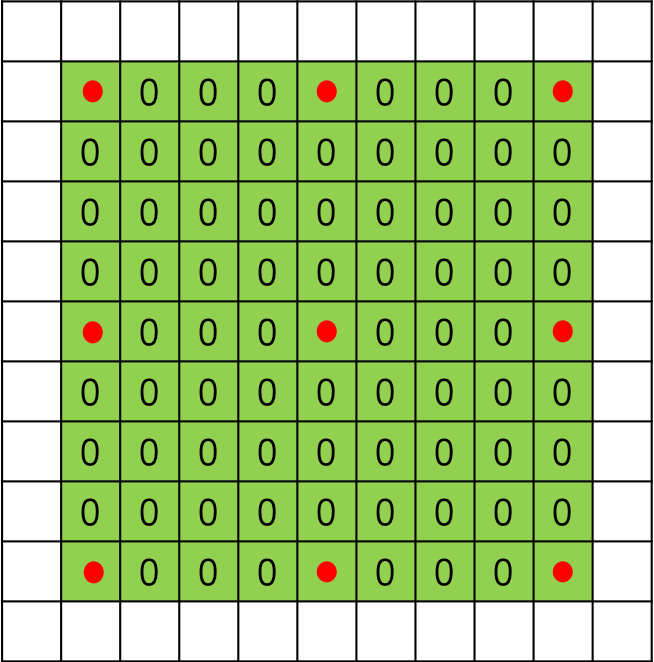
图3 扩张率为4时的3*3空洞卷积
扩张率大于1时,在标准卷积的基础上,会注入空洞,空洞中的数值全部填0。
1.4 空洞卷积的感受野
对于标准卷积而言,当标准卷积核尺寸为 3 × 3 3\times{3} 3×3 时,我们在输入矩阵上连续进行两次标准卷积计算,得到两个特征图。我们可以观察不同层数的卷积核感受野大小,如 图4 所示。
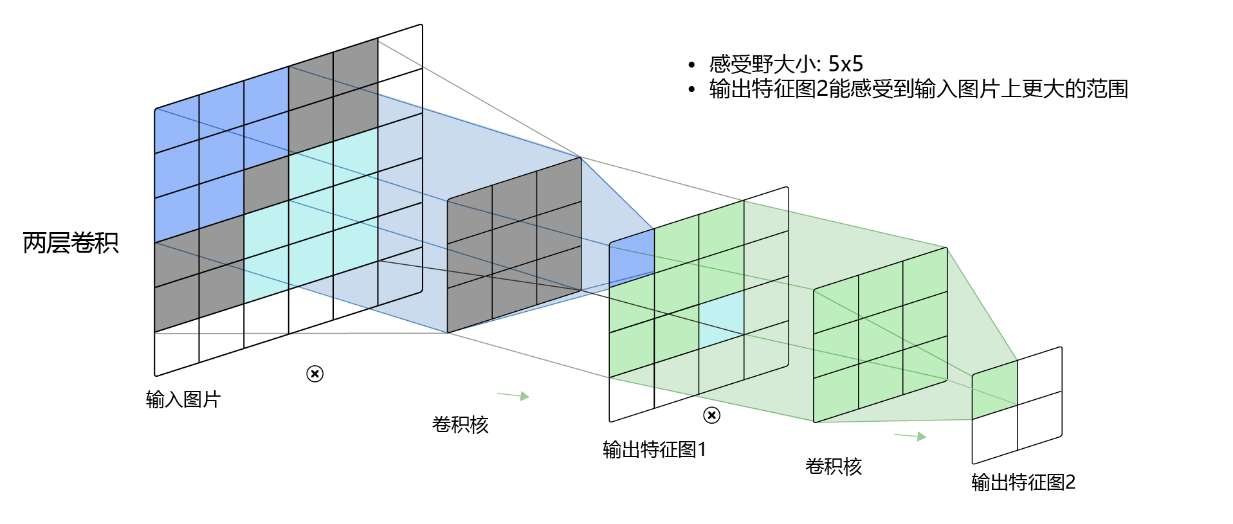
图4 标准卷积的感受野示例
其中, 3 × 3 3\times3 3×3卷积对应的感受野大小就是 3 × 3 3\times3 3×3,而通过两层 3 × 3 3\times3 3×3的卷积之后,感受野的大小将会增加到 5 × 5 5\times5 5×5。
空洞卷积的感受野计算方式与标准卷积大同小异。由于空洞卷积实际上可以看作在标准卷积核内填充’0’,所以我们可以将其想象为一个尺寸变大的标准卷积核,从而使用标准卷积核计算感受野的方式来计算空洞卷积的感受野大小。对于卷积核大小为 k k k ,扩张率为 r r r 的空洞卷积,感受野 F F F 的计算公式为:
F = k + ( k − 1 ) ( r − 1 ) F = k + (k-1)(r-1) F=k+(k−1)(r−1)
卷积核大小 k = 3 k=3 k=3 ,扩张率 r = 2 r=2 r=2 时,计算方式如 图5 所示。
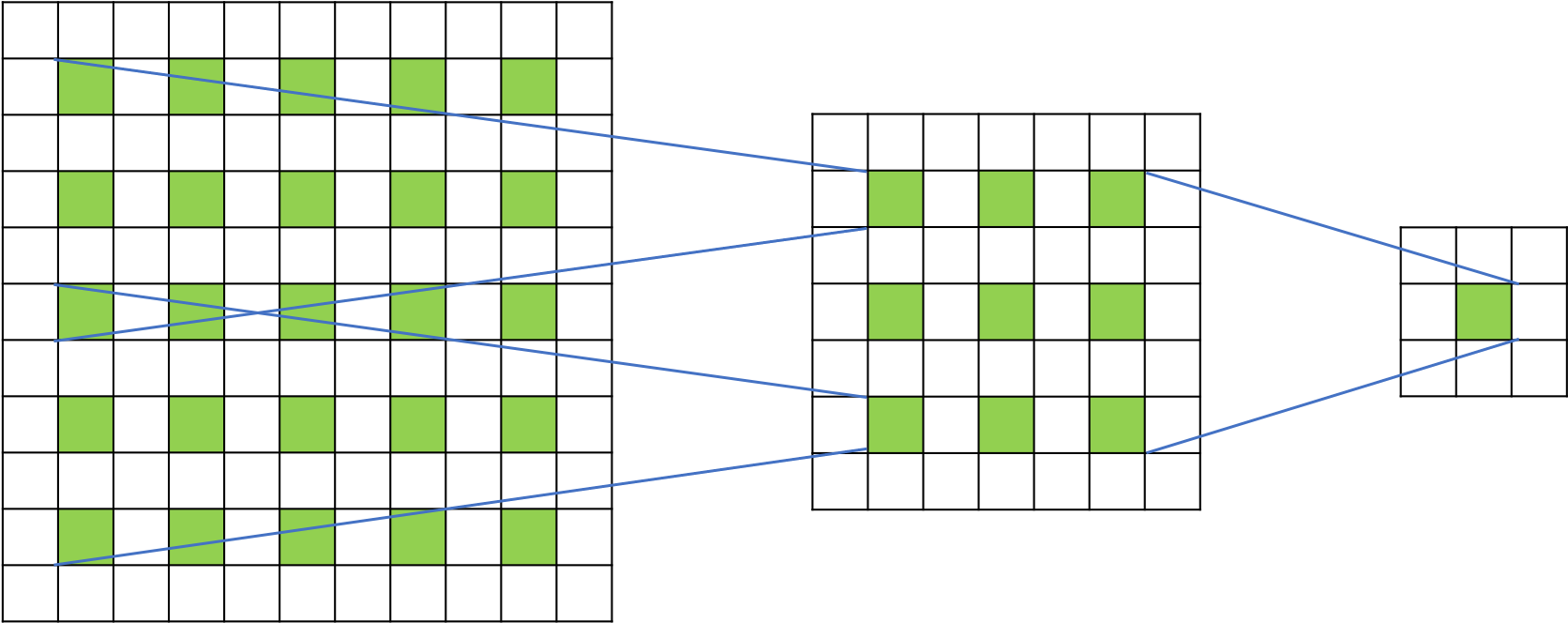
图5 空洞卷积的感受野示例
其中,通过一层空洞卷积后,感受野大小为 5 × 5 5\times5 5×5,而通过两层空洞卷积后,感受野的大小将会增加到 9 × 9 9\times9 9×9。
参考文献
[1] Fully Convolutional Networks for Semantic Segmentation
[2] Semantic image segmentation with deep convolutional nets and fully connected CRFs
[3] DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs
[4] Rethinking Atrous Convolution for Semantic Image Segmentation
[5] Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation
[6] Understanding Convolution for Semantic Segmentation
[7 ] Receptive Field Block Net for Accurate and Fast Object Detection
[8] WaveNet: a generative model for raw audio
2.分组卷积(Group Convolution)
2.1 分组卷积提出背景
分组卷积(Group Convolution)最早出现在AlexNet[1]中。受限于当时的硬件资源,在AlexNet网络训练时,难以把整个网络全部放在一个GPU中进行训练,因此,作者将卷积运算分给多个GPU分别进行计算,最终把多个GPU的结果进行融合。因此分组卷积的概念应运而生。
2.2 分组卷积与标准卷积的区别
对于尺寸为 H 1 × W 1 × C 1 H_1\times{W_1}\times{C_1} H1×W1×C1 的输入矩阵,当标准卷积核的尺寸为 h 1 × w 1 × C 1 h_1\times{w_1}\times{C_1} h1×w1×C1 ,共有 C 2 C_2 C2 个标准卷积核时,标准卷积会对完整的输入数据进行运算,最终得到的输出矩阵尺寸为 H 2 × W 2 × C 2 H_2\times{W_2}\times{C_2} H2×W2×C2 。这里我们假设卷积运算前后的特征图尺寸保持不变,则上述过程可以展示为 图1 。
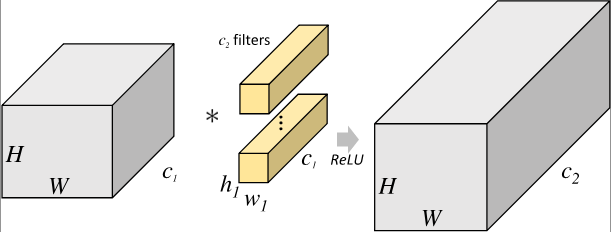
图1 标准卷积示意图
考虑到上述过程是完整运行在同一个设备上,这也对设备的性能提出了较高的要求。
分组卷积则是针对这一过程进行了改进。分组卷积中,通过指定组数 g g g 来确定分组数量,将输入数据分成 g g g 组。需要注意的是,这里的分组指的是在深度上进行分组,输入的宽和高保持不变,即将每 C 1 g \frac{C_1}{g} gC1 个通道的数据分为一组。因为输入数据发生了改变,相应的卷积核也需要进行对应的变化,即每个卷积核的输入通道数也就变为了 C 1 g \frac{C_1}{g} gC1 ,而卷积核的大小是不需要改变的。同时,每组的卷积核个数也由原来的 C 2 C_2 C2 变为 C 2 g \frac{C_2}{g} gC2 。对于每个组内的卷积运算,同样采用标准卷积运算的计算方式,这样就可以得到 g g g 组尺寸为 H 2 × W 2 × C 2 g H_2\times{W_2}\times{\frac{C_2}{g}} H2×W2×gC2 的输出矩阵,最终将这 g g g 组输出矩阵进行拼接就可以得到最终的结果。这样拼接完成后,最终的输出尺寸就可以保持不变,仍然是 H 2 × W 2 × C 2 H_2\times{W_2}\times{C_2} H2×W2×C2 。分组卷积的运算过程如 图2 所示。
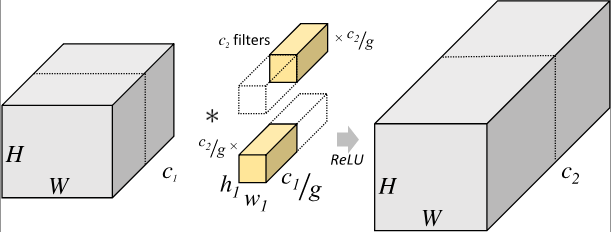
图2 分组卷积示意图
由于我们将整个标准卷积过程拆分成了 g g g 组规模更小的子运算来并行进行,所以最终降低了对运行设备的要求。同时,通过分组卷积的方式,参数量也可以得到降低。在上述的标准卷积中,参数量为:
h 1 × w 1 × C 1 × C 2 h_1 \times w_1 \times C_1 \times C_2 h1×w1×C1×C2
而使用分组卷积后,参数量则变为:
h 1 × w 1 × C 1 g × C 2 g × g = h 1 × w 1 × C 1 × C 2 × 1 g h_1 \times w_1 \times \frac{C_1}{g} \times \frac{C_2}{g} \times g = h_1 \times w_1 \times C_1 \times C_2 \times \frac{1}{g} h1×w1×gC1×gC2×g=h1×w1×C1×C2×g1
2.3 分组卷积应用示例
比如对于尺寸为 H × W × 64 H\times{W}\times{64} H×W×64 的输入矩阵,当标准卷积核的尺寸为 3 × 3 × 64 3\times{3}\times{64} 3×3×64 ,共有 64 64 64 个标准卷积核时,图3 为组数 g = 2 g=2 g=2 时的分组卷积计算方式。
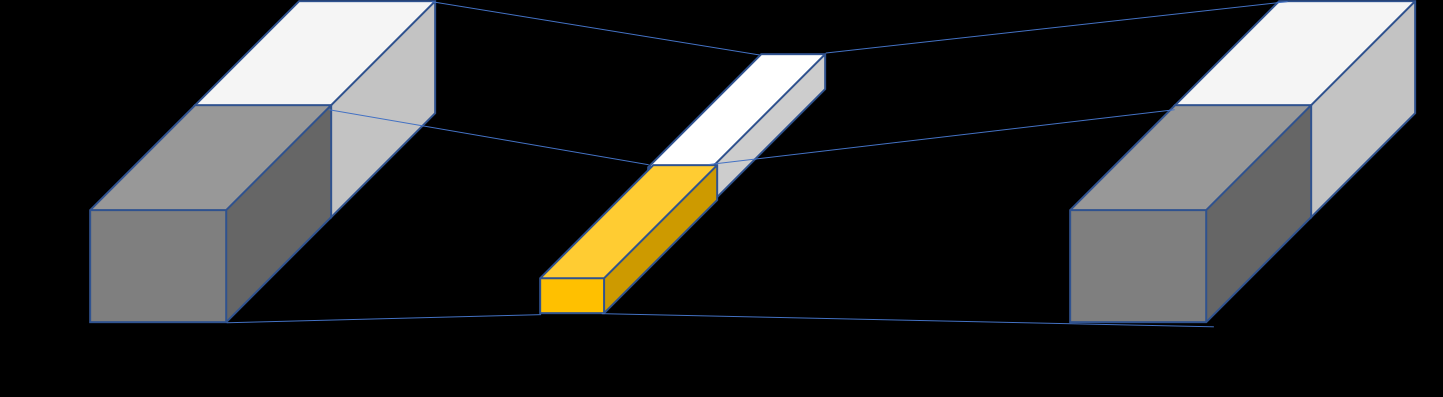
图3 组数为2时分组卷积示意图
此时,每组的输入通道数变为32,卷积核通道数也变为为32。所以,标准卷积对应的参数量是 3 × 3 × 64 × 64 = 36864 3\times{3}\times{64}\times{64}=36864 3×3×64×64=36864 ,而分组卷积的参数量变为 3 × 3 × 32 × 32 × 2 = 18432 3\times{3}\times{32}\times{32}\times{2}=18432 3×3×32×32×2=18432,参数量减少了一半。
参考文献[¶]
[1] ImageNet Classification with Deep Convolutional Neural Networks
© Copyright 2021, nlpers. Revision b063757f.
Built with Sphinx using a theme provided by Read the Docs.
3.可分离卷积(Separable Convolution)
3.1 可分离卷积提出背景
传统的卷积神经网络在计算机视觉领域已经取得了非常好的成绩,但是依然存在一个待改进的问题—计算量大。
当卷积神经网络应用到实际工业场景时,模型的参数量和计算量都是十分重要的指标,较小的模型可以高效地进行分布式训练,减小模型更新开销,降低平台体积功耗存储和计算能力的限制,方便部署在移动端。
因此,为了更好地实现这个需求,在卷积运算的基础上,学者们提出了更为高效的可分离卷积。
3.2 空间可分离卷积
空间分离卷积(spatial separable convolutions),顾名思义就是在空间维度将标准卷积运算进行拆分,将标准卷积核拆分成多个小卷积核。例如我们可以将卷积核拆分成两个(或多个)向量的外积:
[ 3 6 9 4 8 12 5 10 15 ] = [ 3 4 5 ] × [ 1 2 3 ] \begin{split} \left[\begin{array}{ccc} 3 & 6 & 9 \\ 4 & 8 & 12 \\ 5 & 10 & 15 \end{array}\right] = \left[\begin{array}{ccc} 3 \\ 4 \\ 5 \end{array}\right] \times \left[\begin{array}{ccc} 1 \quad 2 \quad 3 \end{array}\right] \end{split} 345681091215 = 345 ×[123]
此时,对于一副输入图像而言,我们就可以先用 3 × 1 3\times1 3×1的 kernel 做一次卷积,再用 1 × 3 1\times3 1×3的 kernel 做一次卷积,从而得到最终结果。具体操作如 图 1 所示。
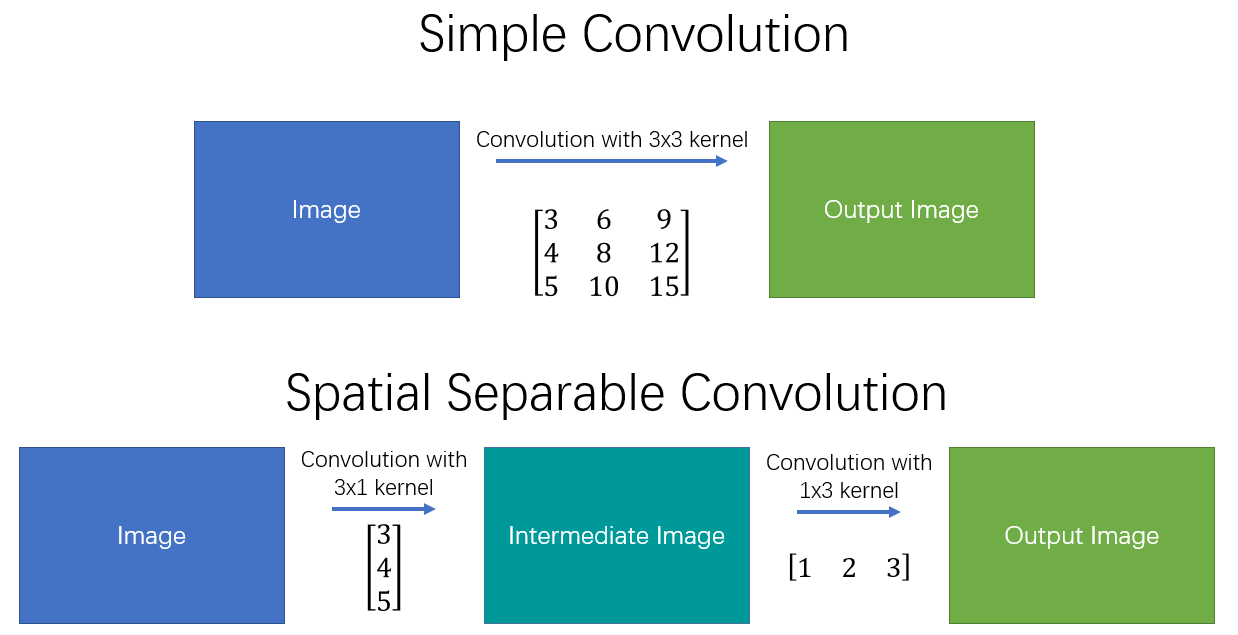
图 1 空间可分离卷积
这样,我们将原始的卷积进行拆分,本来需要 9 次乘法操作的一个卷积运算,就变为了两个需要 3 次乘法操作的卷积运算,并且最终效果是不变的。可想而知,乘法操作减少,计算复杂性就降低了,网络运行速度也就更快了。
但是空间可分离卷积也存在一定的问题,那就是并非所有的卷积核都可以拆分成两个较小的卷积核。 所以这种方法使用的并不多。
3.3 空间可分离卷积应用示例
空间可分离卷积在深度学习中应用较少,在传统图像处理领域比较有名的是可用于边缘检测的 sobel 算子,分离的 sobel 算子计算方式如下:
[ − 1 0 1 − 2 0 2 − 1 0 1 ] = [ 1 2 1 ] × [ − 1 0 1 ] \begin{split} \left[\begin{array}{ccc} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{array}\right] = \left[\begin{array}{ccc} 1 \\ 2 \\ 1 \end{array}\right] \times \left[\begin{array}{ccc} -1 \quad 0 \quad 1 \end{array}\right] \end{split} −1−2−1000121 = 121 ×[−101]
3.4 深度可分离卷积
深度可分离卷积(depthwise separable convolutions)的不同之处在于,其不仅仅涉及空间维度,还涉及深度维度(即 channel 维度)。通常输入图像会具有 3 个 channel:R、G、B。在经过一系列卷积操作后,输入特征图就会变为多个 channel。对于每个 channel 而言,我们可以将其想成对该图像某种特定特征的解释说明。例如输入图像中,“红色” channel 解释描述了图像中的 “红色” 特征,“绿色” channel 解释描述了图像中的 “绿色” 特征,“蓝色” channel 解释描述了图像中的 “蓝色” 特征。又例如 channel 数量为 64 的输出特征图,就相当于对原始输入图像的 64 种不同的特征进行了解释说明。
类似空间可分离卷积,深度可分离卷积也是将卷积核分成两个单独的小卷积核,分别进行 2 种卷积运算:深度卷积运算和逐点卷积运算。 首先,让我们看看正常的卷积是如何工作的。
3.4.1标准卷积
假设我们有一个 12 × 12 × 3 12\times 12\times 3 12×12×3 的输入图像,即图像尺寸为 12 × 12 12\times 12 12×12,通道数为 3,对图像进行 5 × 5 5\times 5 5×5 卷积,没有填充(padding)且步长为 1。如果我们只考虑图像的宽度和高度,使用 5 × 5 5\times 5 5×5 卷积来处理 12 × 12 12\times 12 12×12 大小的输入图像,最终可以得到一个 8 × 8 8\times 8 8×8 的输出特征图。然而,由于图像有 3 个通道,我们的卷积核也需要有 3 个通道。 这就意味着,卷积核在每个位置进行计算时,实际上会执行 5 × 5 × 3 = 75 5\times 5\times 3=75 5×5×3=75 次乘法。如 图 2 所示,我们使用一个 5 × 5 × 3 5\times 5\times 3 5×5×3 的卷积核进行卷积运算,最终可以得到 8 × 8 × 1 8\times 8\times 1 8×8×1 的输出特征图。

图 2 输出通道为 1 的标准卷积
如果我们想增加输出的 channel 数量让网络学习更多种特征呢?这时我们可以创建多个卷积核,比如 256 个卷积核来学习 256 个不同类别的特征。此时,256 个卷积核会分别进行运算,得到 256 个 8 × 8 × 1 8\times 8\times 1 8×8×1 的输出特征图,将其堆叠在一起,最终可以得到 8 × 8 × 256 8\times 8\times 256 8×8×256 的输出特征图。如 图 3 所示。
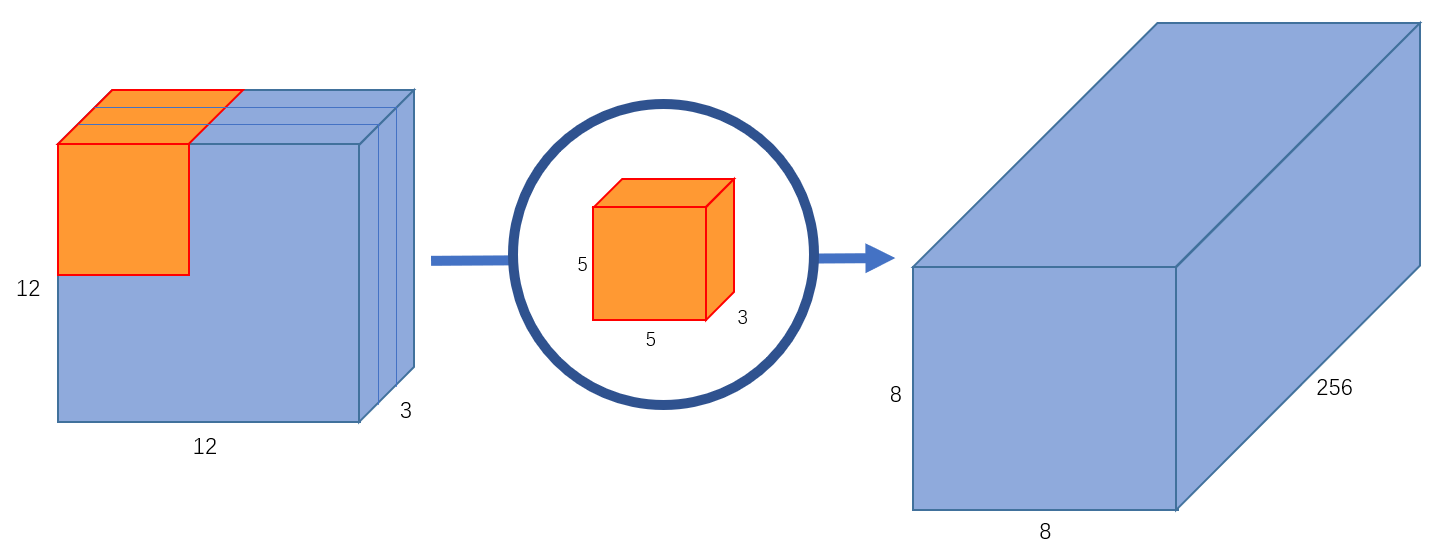
图 3 输出通道为 256 的标准卷积
接下来,再来看一下如何通过深度可分离卷积得到 8 × 8 × 256 8\times 8\times 256 8×8×256 的输出特征图。
3.4.2 深度卷积运算
首先,我们对输入图像进行深度卷积运算,这里的深度卷积运算其实就是逐通道进行卷积运算。对于一幅 12 × 12 × 3 12\times 12\times 3 12×12×3 的输入图像而言,我们使用大小为 5 × 5 5\times 5 5×5 的卷积核进行逐通道运算,计算方式如 图 4 所示。
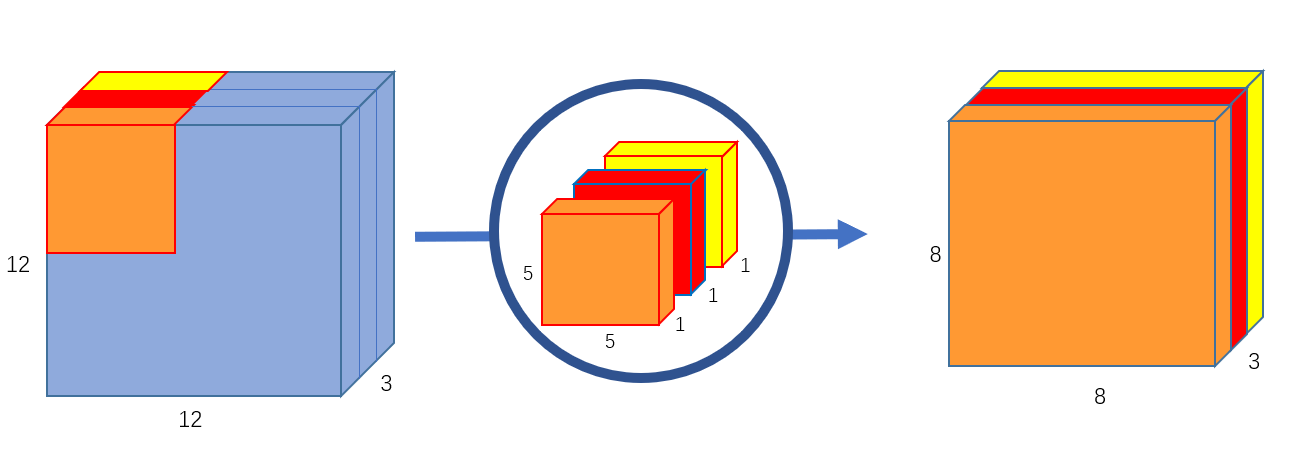
图 4 深度卷积运算
这里其实就是使用 3 个 5 × 5 × 1 5\times 5\times 1 5×5×1 的卷积核分别提取输入图像中 3 个 channel 的特征,每个卷积核计算完成后,会得到 3 个 8 × 8 × 1 8\times 8\times 1 8×8×1 的输出特征图,将这些特征图堆叠在一起就可以得到大小为 8 × 8 × 3 8\times 8\times 3 8×8×3 的最终输出特征图。这里我们可以发现深度卷积运算的一个缺点,深度卷积运算缺少通道间的特征融合 ,并且运算前后通道数无法改变。
因此,接下来就需要连接一个逐点卷积来弥补它的缺点。
3.4.3逐点卷积运算
前面我们使用深度卷积运算完成了从一幅 12 × 12 × 3 12\times 12\times 3 12×12×3 的输入图像中得到 8 × 8 × 3 8\times 8\times 3 8×8×3 的输出特征图,并且发现仅使用深度卷积无法实现不同通道间的特征融合,而且也无法得到与标准卷积运算一致的 8 × 8 × 256 8\times 8\times 256 8×8×256 的特征图。那么,接下来就让我们看一下如何使用逐点卷积实现这两个任务。
逐点卷积其实就是 1 × 1 1\times 1 1×1 卷积,因为其会遍历每个点,所以我们称之为逐点卷积。 1 × 1 1\times 1 1×1 卷积在前面的内容中已经详细介绍了,这里我们还是结合上边的例子看一下它的具体作用。
我们使用一个 3 通道的 1 × 1 1\times 1 1×1 卷积对上文中得到的 8 × 8 × 3 8\times 8\times 3 8×8×3 的特征图进行运算,可以得到一个 8 × 8 × 1 8\times 8\times 1 8×8×1 的输出特征图。如 图 5 所示。此时,我们就使用逐点卷积实现了融合 3 个通道间特征的功能。
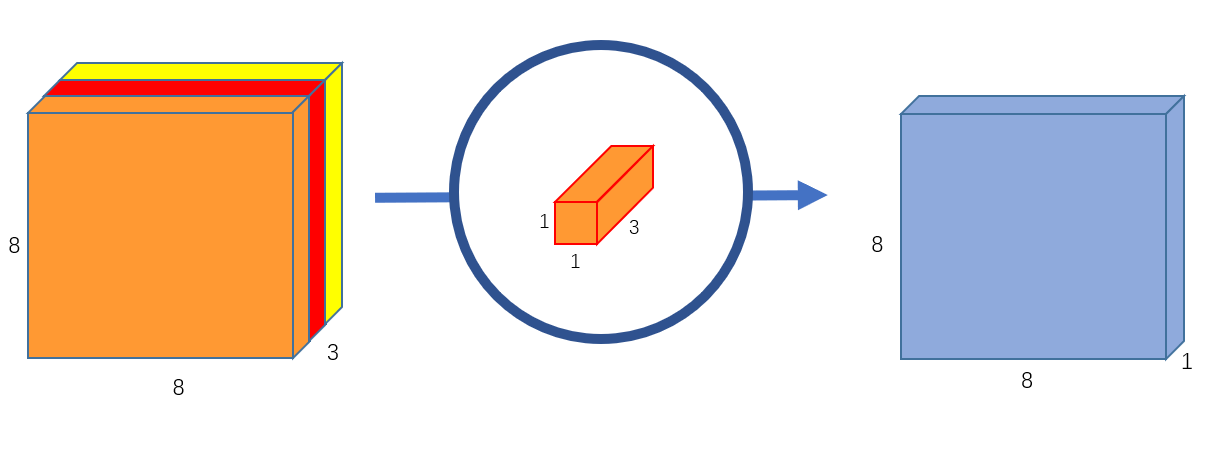
图 5 输出通道为 1 的逐点卷积
此外,我们可以创建 256 个 3 通道的 1 × 1 1\times 1 1×1 卷积对上文中得到的 8 × 8 × 3 8\times 8\times 3 8×8×3 的特征图进行运算,这样,就可以实现得到与标准卷积运算一致的 8 × 8 × 256 8\times 8\times 256 8×8×256 的特征图的功能。如 图 6 所示。
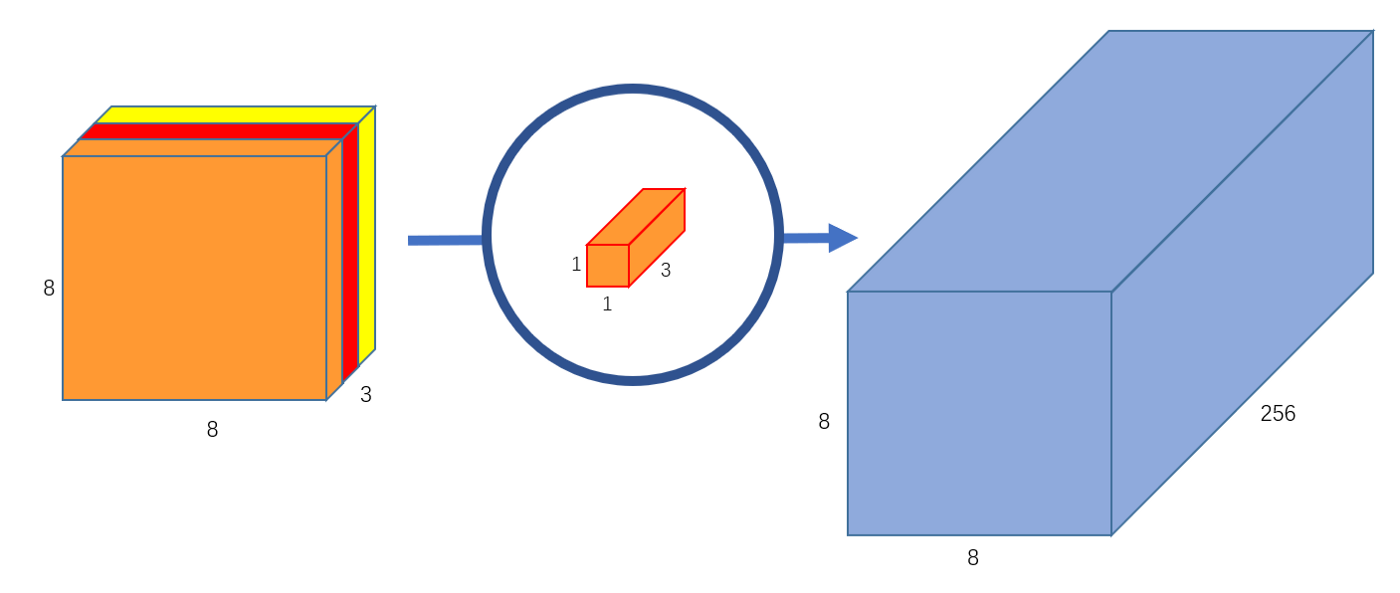
图 6 输出通道为 256 的逐点卷积
3.4.4 深度可分离卷积的意义
上文中,我们给出了深度可分离卷积的具体计算方式,那么使用深度可分离卷积代替标准卷积有什么意义呢?
这里我们看一下上文例子中标准卷积的乘法运算个数,我们创建了 256 个 5 × 5 × 3 5\times 5\times 3 5×5×3 的卷积核进行卷积运算,每个卷积核会在输入图片上移动 8 × 8 8\times 8 8×8 次,因此总的乘法运算个数为:
256 × 3 × 5 × 5 × 8 × 8 = 1228800 256 \times 3 \times 5 \times 5 \times 8 \times 8=1228800 256×3×5×5×8×8=1228800
而换成深度可分离卷积后,在深度卷积运算时,我们使用 3 个 5 × 5 × 1 5\times 5\times 1 5×5×1 的卷积核在输入图片上移动 8 × 8 8\times 8 8×8 次,此时乘法运算个数为:
3 × 5 × 5 × 8 × 8 = 4800 3 \times 5 \times 5 \times 8 \times 8=4800 3×5×5×8×8=4800
在逐点卷积运算时,我们使用 256 个 1 × 1 × 3 1\times 1\times 3 1×1×3 的卷积在输入特征图上移动 8 × 8 8\times 8 8×8 次,此时乘法运算个数为:
256 × 1 × 1 × 3 × 8 × 8 = 49152 256 \times 1 \times 1 \times 3 \times 8 \times 8=49152 256×1×1×3×8×8=49152
将这两步运算相加,即可得到,使用深度可分离卷积后,总的乘法运算个数变为:53952。可以看到,深度可分离卷积的运算量相较标准卷积而言,计算量少了很多。
3.4.5深度可分离卷积应用示例
MobileNetv1[1] 中使用的深度可分离卷积如 图 7 右侧所示。相较于左侧的标准卷积,其进行了拆分,同时使用了 BN 层以及 RELU 激活函数穿插在深度卷积运算和逐点卷积运算中。
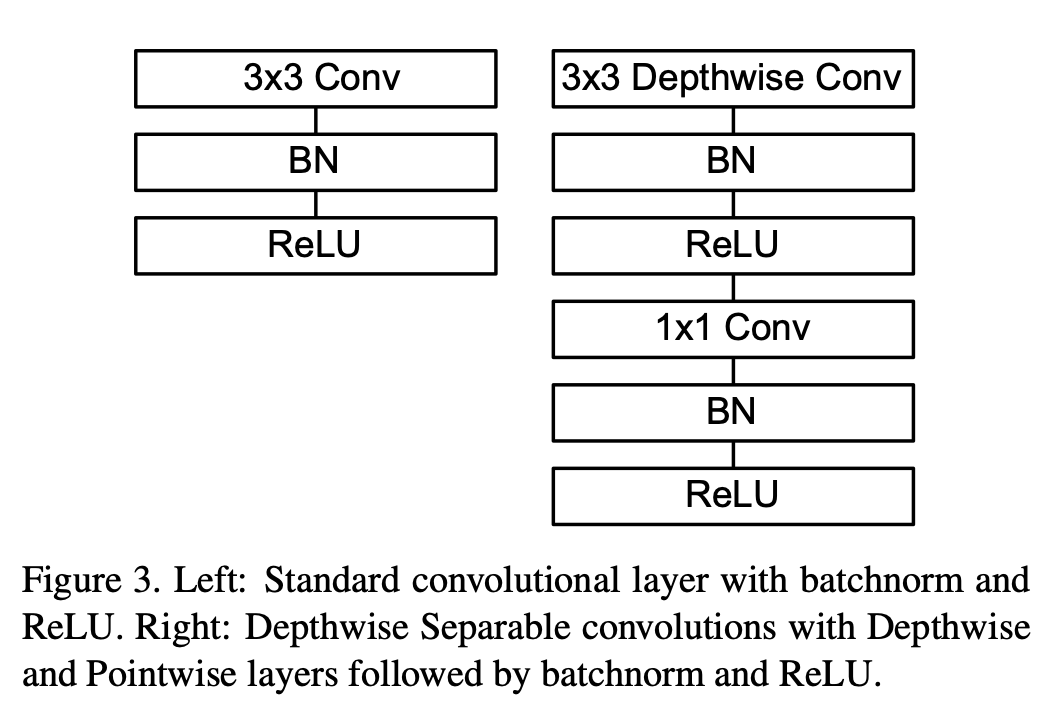
图 7 MobileNetv1 中的可分离卷积
参考文献 ¶
[1] MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications
4.可变形卷积详解
4.1 提出背景
视觉识别的一个关键挑战是如何适应物体尺度、姿态、视点和零件变形的几何变化或模型几何变换。
但对于视觉识别的传统CNN模块,不可避免的都存在固定几何结构的缺陷:卷积单元在固定位置对输入特征图进行采样;池化层以固定比率降低空间分辨率;一个ROI(感兴趣区域)池化层将一个ROI分割成固定的空间单元;缺乏处理几何变换的内部机制等。
这些将会引起一些明显的问题。例如,同一CNN层中所有激活单元的感受野大小是相同的,这对于在空间位置上编码语义的高级CNN层是不需要的。而且,对于具有精细定位的视觉识别(例如,使用完全卷积网络的语义分割)的实际问题,由于不同的位置可能对应于具有不同尺度或变形的对象,因此,尺度或感受野大小的自适应确定是可取的。
为了解决以上所提到的局限性,一个自然地想法就诞生了:卷积核自适应调整自身的形状。这就产生了可变形卷积的方法。
4.2 可变形卷积
4.2.1 DCN v1
可变形卷积顾名思义就是卷积的位置是可变形的,并非在传统的 N × N N × N N×N的网格上做卷积,这样的好处就是更准确地提取到我们想要的特征(传统的卷积仅仅只能提取到矩形框的特征),通过一张图我们可以更直观地了解:
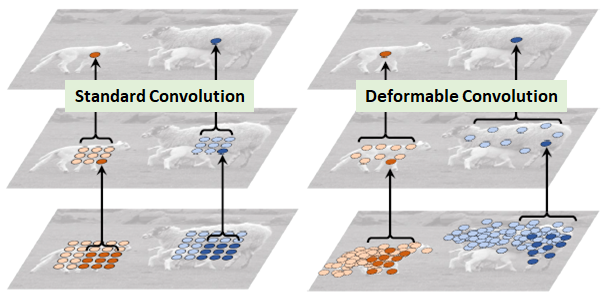
图1 绵羊特征提取
在上面这张图里面,左边传统的卷积显然没有提取到完整绵羊的特征,而右边的可变形卷积则提取到了完整的不规则绵羊的特征。
那可变卷积实际上是怎么做的呢?其实就是在每一个卷积采样点加上了一个偏移量,如下图所示:
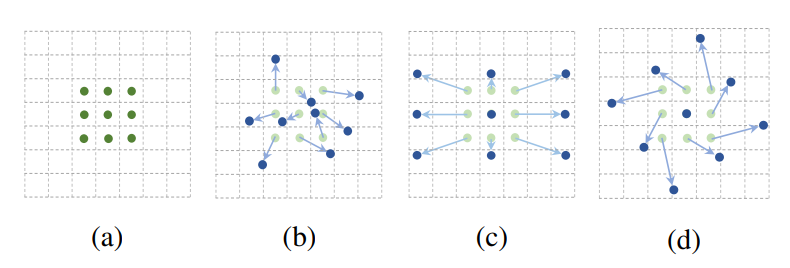
图2 卷积核和可变形卷积核
(a) 所示的正常卷积规律的采样 9 个点(绿点);(b)©(d) 为可变形卷积,在正常的采样坐标上加上一个位移量(蓝色箭头);其中 (d) 作为 (b) 的特殊情况,展示了可变形卷积可以作为尺度变换,比例变换和旋转变换等特殊情况。
普通的卷积,以 3 × 3 3\times3 3×3卷积为例对于每个输出 y ( p 0 ) y_(\mathrm{p}_0) y(p0),都要从 x x x上采样9个位置,这9个位置都在中心位置 x ( p 0 ) \mathrm{x}(p0) x(p0)向四周扩散, ( − 1 , − 1 ) (-1,-1) (−1,−1)代表 x ( p 0 ) \mathrm{x}(p0) x(p0)的左上角, ( 1 , 1 ) (1,1) (1,1)代表 x ( p 0 ) \mathrm{x}(p0) x(p0)的右下角。
R = { ( − 1 , − 1 ) , ( − 1 , 0 ) , . . . , ( 0 , 1 ) , ( 1 , 1 ) } \mathrm{R} = \{(-1,-1),(-1,0),...,(0,1),(1,1)\} R={(−1,−1),(−1,0),...,(0,1),(1,1)}
所以传统卷积的输出就是(其中 p n \mathrm{p}_n pn就是网格中的 n n n个点, w ( p n ) \mathrm{w}(\mathrm{p}_n) w(pn)表示对应点位置的卷积权重系数): $ y ( p 0 ) = ∑ p n ∈ R w ( p n ) ⋅ x ( p 0 + p n ) y(\mathrm{p}_0)=\sum_{\mathrm{p}_n\in\mathrm{R}}\mathrm{w}(\mathrm{p}_n) \cdot \mathrm{x}(\mathrm{p}_0+\mathrm{p}_n) y(p0)=∑pn∈Rw(pn)⋅x(p0+pn) $
正如上面阐述的可变形卷积,就是在传统的卷积操作上加入了一个偏移量 Δ p n \Delta \mathrm{p}_n Δpn,正是这个偏移量才让卷积变形为不规则的卷积,这里要注意这个偏移量可以是小数,所以下面的式子的特征值需要通过_双线性插值_的方法来计算。
y ( p 0 ) = ∑ p n ∈ R w ( p n ) ⋅ x ( p 0 + p n + Δ p n ) y(\mathrm{p}_0)=\sum_{\mathrm{p}_n\in\mathrm{R}}\mathrm{w}(\mathrm{p}_n) \cdot \mathrm{x}(\mathrm{p}_0+\mathrm{p}_n+\Delta \mathrm{p}_n) y(p0)=pn∈R∑w(pn)⋅x(p0+pn+Δpn)
那这个偏移量如何算呢?我们来看:
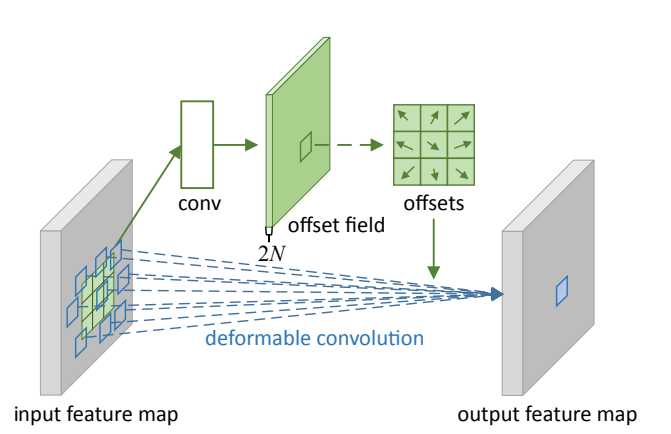
图3 3x3 deformable convolution
对于输入的一张feature map,假设原来的卷积操作是 3 × 3 3\times3 3×3的,那么为了学习偏移量offset,我们定义另外一个 3 × 3 3\times3 3×3的卷积层(图中上面的那层),输出的维度其实就是原来feature map大小,channel数等于 2 N 2N 2N(分别表示 x , y x,y x,y方向的偏移)。下面的可变形卷积可以看作先基于上面那部分生成的offset做了一个插值操作,然后再执行普通的卷积。
4.2.2 DCN v2
DCN v2 在DCN v1基础(添加offset)上添加每个采样点的权重
为了解决引入了一些无关区域的问题,在DCN v2中我们不只添加每一个采样点的偏移,还添加了一个权重系数 Δ m k \Delta m_k Δmk,来区分我们引入的区域是否为我们感兴趣的区域,假如这个采样点的区域我们不感兴趣,则把权重学习为0即可:
y ( p 0 ) = ∑ p n ∈ R w ( p n ) ⋅ x ( p 0 + p n + Δ p n ) ⋅ Δ m k y(\mathrm{p}_0)=\sum_{\mathrm{p}_n\in\mathrm{R}}\mathrm{w}(\mathrm{p}_n) \cdot \mathrm{x}(\mathrm{p}_0+\mathrm{p}_n+\Delta \mathrm{p}_n) \cdot \Delta m_k y(p0)=pn∈R∑w(pn)⋅x(p0+pn+Δpn)⋅Δmk
paddle中的API
paddle.vision.ops.deform_conv2d(*x*, *offset*, *weight*, *bias=None*, *stride=1*, *padding=0*, *dilation=1*, *deformable_groups=1*, *groups=1*, *mask=None*, *name=None*);
deform_conv2d 对输入4-D Tensor计算2-D可变形卷积。详情参考deform_conv2d。
核心参数解析:
-
x (Tensor) - 形状为 ( N , C , H , W ) (N,C,H,W) (N,C,H,W)的输入Tensor,数据类型为float32或float64。
-
offset (Tensor) – 可变形卷积层的输入坐标偏移,数据类型为float32或float64。
-
weight (Tensor) – 卷积核参数,形状为 M , C / g , k H , k W ] M,C/g,k_H,k_W] M,C/g,kH,kW], 其中 M 是输出通道数, g g g 是group组数, k H k_H kH是卷积核高度尺寸, k W k_W kW是卷积核宽度尺寸。数据类型为float32或float64。
-
stride (
int|list|tuple,可选) - 步长大小。卷积核和输入进行卷积计算时滑动的步长。如果它是一个列表或元组,则必须包含两个整型数:(stride_height,stride_width)。若为一个整数,stride_height = stride_width = stride。默认值:1。 -
padding (
int|list|tuple,可选) - 填充大小。卷积核操作填充大小。如果它是一个列表或元组,则必须包含两个整型数:(padding_height,padding_width)。若为一个整数,padding_height = padding_width = padding。默认值:0。 -
mask (Tensor, 可选) – 可变形卷积层的输入掩码,当使用可变形卷积算子v1时,请将mask设置为None, 数据类型为float32或float64。
输入:
-
input 形状: ( N , C i n , H i n , W i n ) (N,C_{in},H_{in},W_{in}) (N,Cin,Hin,Win)
-
weight形状: ( C o u t , C i n , H f , W f ) (C_{out},C_{in},H_f,W_f) (Cout,Cin,Hf,Wf)
-
offset形状: ( N , 2 ∗ H f ∗ W f , H o u t , W o u t ) (N,2*H_f*W_f,H_{out},W_{out}) (N,2∗Hf∗Wf,Hout,Wout)
-
mask形状: ( N , H f ∗ W f , H o u t , W o u t ) (N,H_f*W_f,H_{out},W_{out}) (N,Hf∗Wf,Hout,Wout)
输出:
- output形状: ( N , C o u t , H o u t , W o u t ) (N,C_{out},H_{out},W_{out}) (N,Cout,Hout,Wout)
其中:
H o u t = ( H i n + 2 ∗ p a d d i n g s [ 0 ] − ( d i l a t i o n s [ 0 ] ∗ ( H f − 1 ) + 1 ) ) s t r i d e s [ 0 ] + 1 W o u t = ( W i n + 2 ∗ p a d d i n g s [ 1 ] − ( d i l a t i o n s [ 1 ] ∗ ( W f − 1 ) + 1 ) ) s t r i d e s [ 1 ] + 1 \begin{split} H_{out}=\frac{(H_{in}+2*paddings[0]-(dilations[0]*(H_f-1)+1))} {strides[0]}+1 \\ W_{out}=\frac{(W_{in}+2*paddings[1]-(dilations[1]*(W_f-1)+1))} {strides[1]}+1 \end{split} Hout=strides[0](Hin+2∗paddings[0]−(dilations[0]∗(Hf−1)+1))+1Wout=strides[1](Win+2∗paddings[1]−(dilations[1]∗(Wf−1)+1))+1
算法实例:
#deformable conv v2:
import paddle
input = paddle.rand((8, 1, 28, 28))
kh, kw = 3, 3
weight = paddle.rand((16, 1, kh, kw))
# offset shape should be [bs, 2 * kh * kw, out_h, out_w]
# mask shape should be [bs, hw * hw, out_h, out_w]
# In this case, for an input of 28, stride of 1
# and kernel size of 3, without padding, the output size is 26
offset = paddle.rand((8, 2 * kh * kw, 26, 26))
mask = paddle.rand((8, kh * kw, 26, 26))
out = paddle.vision.ops.deform_conv2d(input, offset, weight, mask=mask)
print(out.shape)
# returns
[8, 16, 26, 26]
#deformable conv v1: 无mask参数
import paddle
input = paddle.rand((8, 1, 28, 28))
kh, kw = 3, 3
weight = paddle.rand((16, 1, kh, kw))
# offset shape should be [bs, 2 * kh * kw, out_h, out_w]
# In this case, for an input of 28, stride of 1
# and kernel size of 3, without padding, the output size is 26
offset = paddle.rand((8, 2 * kh * kw, 26, 26))
out = paddle.vision.ops.deform_conv2d(input, offset, weight)
print(out.shape)
# returns
[8, 16, 26, 26]
说明:
-
对于每个input的图片数据都是 ( C , H i n , W i n ) (C,H_{in},W_{in}) (C,Hin,Win)类型的数据,其中offset和mask(如果有)中的 H o u t H_{out} Hout和 W o u t W_{out} Wout表示的是输出图片的feature数据格式高和宽。
-
对于每个input图片数据数据对应的输出feature map图中每一个输出的特征位置都有对应的一个大小为 2 ∗ H f ∗ W f 2*H_f*W_f 2∗Hf∗Wf的偏移项和 H f ∗ W f H_f*W_f Hf∗Wf的掩膜项。这样的大小设置是因为偏移项对应的是我们采样的有 H f ∗ W f H_f*W_f Hf∗Wf个点,每个点都有对应的两个偏移方向和一个重要程度。前者就对应了我们的偏移项,后者就对应了掩膜项。
-
算法的过程可以理解为以下三个步骤:
-
通过offset获取对应输出位置的偏移数据,进行采样点的偏移
-
正常使用卷积核对偏移后的采样点进行卷积操作
-
使用mask对卷积的输出进行对应位置相乘 ,这决定了不同位置的关注程度
-
4.3 实例效果
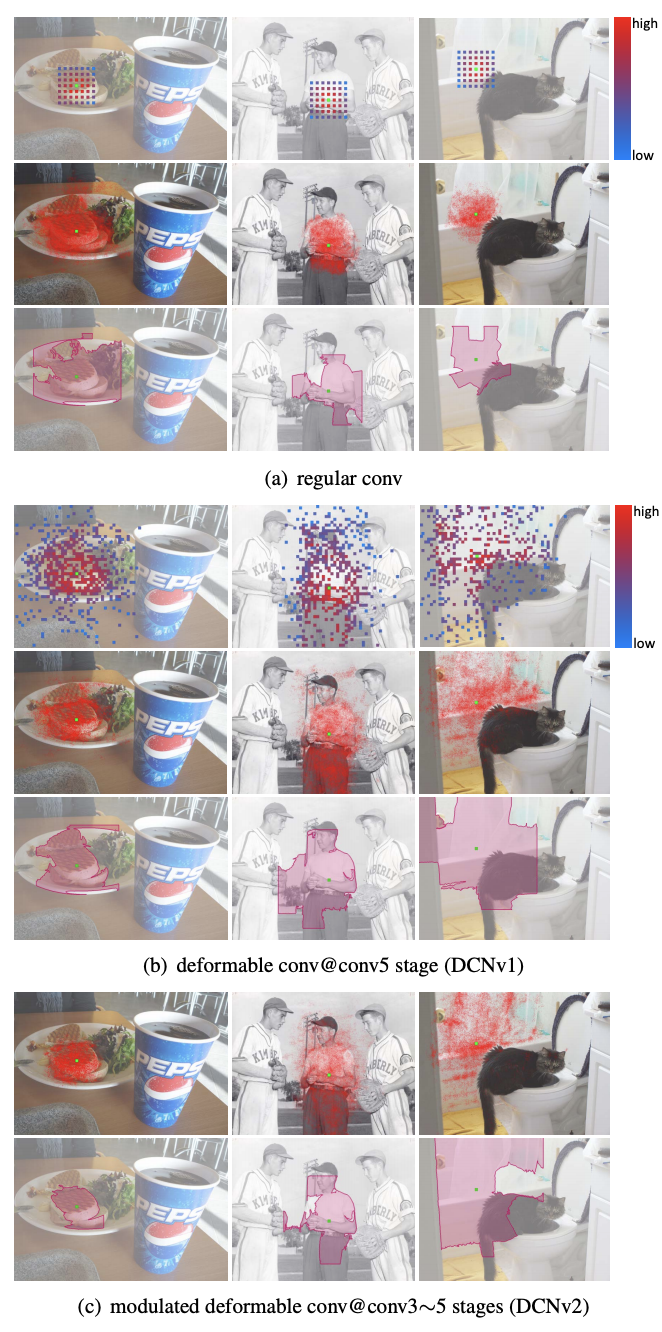
图4 regular、DCN v1、DCN v2的感受野对比
可以从上图4看到,可以看到当绿色点在目标上时,红色点所在区域也集中在目标位置,并且基本能够覆盖不同尺寸的目标,因此经过可变形卷积,我们可以更好地提取出感兴趣物体的完整特征,效果是非常不错的。
但DCN v1听起来不错,但其实也有问题:我们的可变形卷积有可能引入了无用的上下文(区域)来干扰我们的特征提取,这显然会降低算法的表现。通过上图4的对比实验结果(多边形区域框)我们也可以看到DCN v2更能集中在物体的完整有效的区域
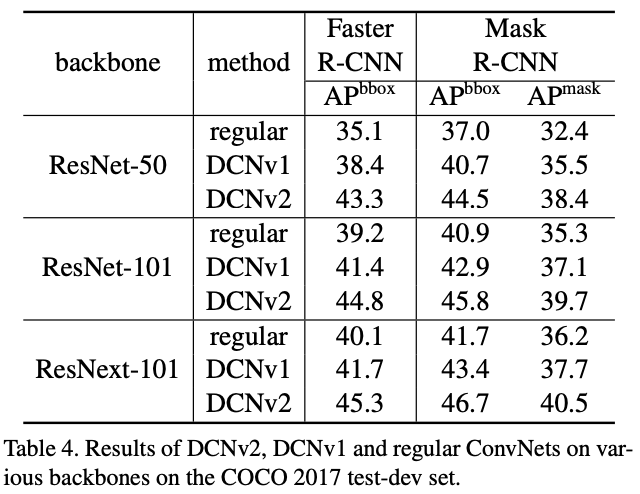
图5 regular、DCN v1、DCN v2的准确率对比
使用可变形卷积,可以更加高效的从图片中获取到目标的特征信息,可以起到提升传统卷积神经网络(如ResNet、Faster R-CNN等)识别和分割上的性能。如以上图5,可以将ResNet等网络中的
3
×
3
3\times3
3×3 标准卷积操作更改为
3
×
3
3\times3
3×3 可变形卷积操作,通过研究发现只要增加很少的计算量,就可以得到较大幅度的性能提升。
总结来说,DCN v1中引入的offset是要寻找有效信息的区域位置,DCN v2中引入权重系数是要给找到的这个位置赋予权重,这两方面保证了有效信息的准确提取。
参考文献
[1] Dai J , Qi H , Xiong Y , et al. Deformable Convolutional Networks[J]. IEEE, 2017.
[2] Zhu X , Hu H , Lin S , et al. Deformable ConvNets V2: More Deformable, Better Results[C]// 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). IEEE, 2019.
[3] https://blog.csdn.net/cristiano20/article/details/107931844
[4] https://www.zhihu.com/question/303900394/answer/540818451
[5] https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/vision/ops/deform_conv2d_cn.html