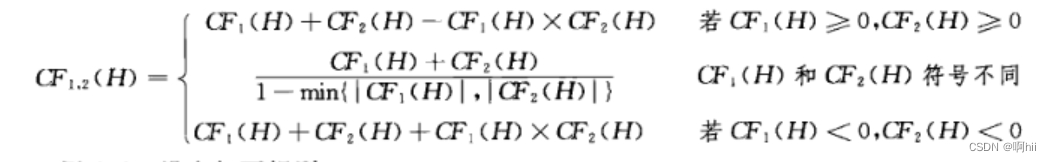注释部分只是复习用,不是答案
第五题

注释:便于复习
本来想搜个类似的,结果发现r1这种人家都带括号!!!额,没括号那我就从前往后算了,按顺序算准没错~
CF(H)的合成公式:
解:推理网络如下图:
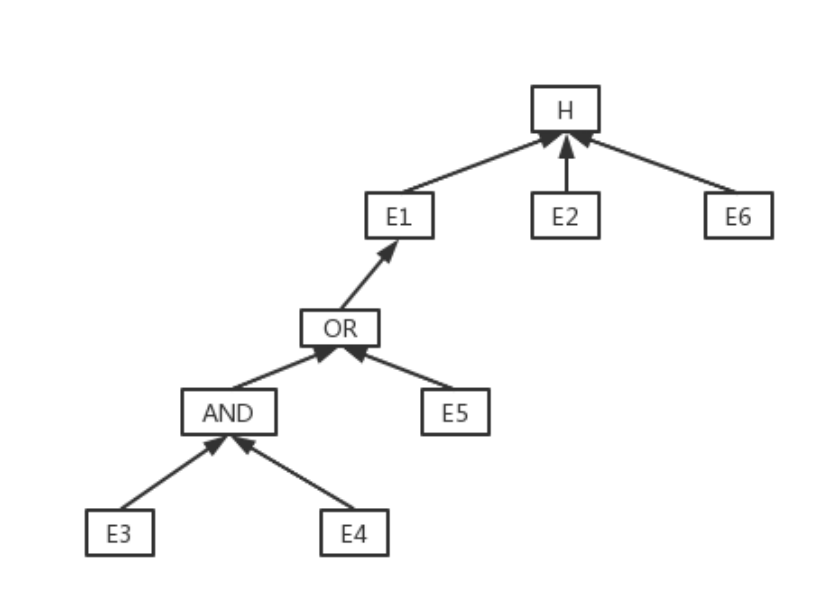
由r1可得:
CF(E1)=CF(E1,E3∧E4∨E5) × CF(E3∧E4∨E5)
=0.8 × max{0,CF(E3∧E4∨E5)}
=0.8 × max{0,max{CF(E3∧E4),CF(E5)}}
=0.8 × max{0,max{min{CF(E3),CF(E4)},CF(E5)}}
=0.8 × max{0,max{0.8,0.6}}
=0.8 × 0.8
=0.64
由r2可得:
CF1(H)=CF(H,E1) × CF(E1)
=0.6 × 0.64
=0.384
由r3可得:
CF2(H)=CF(H,E2) × CF(E2)
=0.7 × 0.6
=0.42
由r4可得:
CF3(H)=CF(H,E6) × CF(E6)
=0.8 × 0.4
=0.32
因为 CF1(H)、CF2(H)、CF3(H)都大于0,所以
CF1,2(H)=0.384 + 0.42 -0.384 × 0.42 = 0.64272
CF(H)=0.64272 + 0.32 - 0.64272 × 0.32 = 0.7570496
第七题

注释:便与复习:
额,最开始在想怎么算出其他m(A),后来懂了才晓得不存在的就是0,其他存在的加起来正好为1!!这样就没问题了。
解:集合有{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c},∅
则有:
(1)
m({a})=0.4
m({b})=0
m({c})=0
m({a,b})=0
m({a,c})=0.4
m({b,c})=0
m(∅)=0
m({a,b,c})=0.2
(2)
Bel({a})=m({a})=0.4
Bel({b})=m({b})=0
Bel({c})=m({c})=0
Bel({a,b})=m({a}) + m({b}) + m({a,b})=0.4
Bel({a,c})=m({a}) + m({c}) + m({a,c})=0.8
Bel({b,c})=m({b}) + m({c}) + m({b,c})=0
Bel({a,b,c})=m({a}) + m({b}) + m({c}) + m({a,b}) + m({a,c}) + m({b,c}) + m({a,b,c})=1
(3)
Pl({a})=1-Bel({a}’)=1-Bel({b,c})=1
Pl({b})=1-Bel({b}’)=1-Bel({a,c})=0.2
Pl({c})=1-Bel({c}’)=1-Bel({a,b})=0.6
Pl({a,b})=1-Bel({a,b}’)=1-Bel({c})=1
Pl({a,c})=1-Bel({a,c}’)=1-Bel({b})=1
Pl({b,c})=1-Bel({b,c}’)=1-Bel({a})=0.6
Pl({a,b,c})=1-Bel({a,b,c}’)=1-Bel(∅)=1
Pl(∅)=1-Bel(∅’)=1-Bel({a,b,c})=0
第九题

解:利用关系合成来构造模糊关系Rm:

注释:写一个思路,便于复习
Rm怎么算出来的,简单来说就是A代表行,B代表列
例如:第2行第3列元素的求法
Rm(2,3)=max{ min{ A(2),B(3)},(1-A(2))}
由已知条件可得:
A’ = {1,0.7,0.5,0.2,0,0}
与模糊关系进行合成得到结论的模糊集合:
B’ = A’ ∘ Rm = (0.4,0.4,0.5,0.7,0.9,1)
注释:写一个思路,便于复习
算出A’ ∘ Rm有两种方法,便于学习只放一种:
合成方法就是取A’的第i行元素分别与Rm第j列的对应元素相比较,两个数中取其小者,然后再在所得的一组数中取最大者,并以此数作为A’ ∘ Rm第i行、第j列的元素。
例如这个题目中:算一下第一行第一列的元素
A’ = {1,0.7,0.5,0.2,0,0}
B’=max{min{1,0},min{0.7,0.2},min{0.5,0.4},min{0.2,0.7},min{0,1},min{0,1}}
(看A的第一行和Rm的第一列,就很easy了!)
即模糊结论y为:
B’ = 0.4/1 + 0.4/2 + 0.5/3 + 0.7/4 + 0.9/5 + 1/6