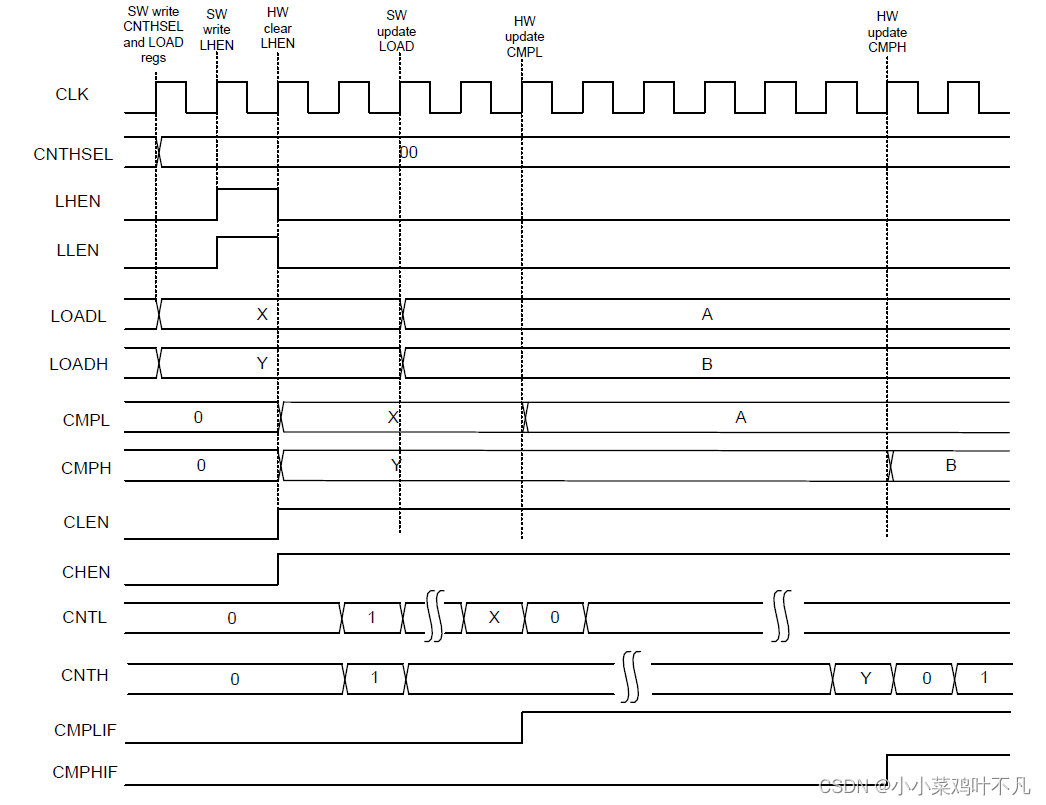
值迭代

通过上一章的学习,我们知道了贝尔曼最优方程的求解实际上分两部分,一是给定一个初始值
v
k
v_k
vk 找到最优策略
π
k
+
1
π_{k+1}
πk+1 ,二是更新
v
k
+
1
v_{k+1}
vk+1

下面,我们将详细剖析这个算法,以及其编程实现。首先,我们来看一下他的第一步:策略更新

通过给定的
v
k
v_k
vk 可以求得每个状态对应的
q
k
q_k
qk 再根据概率设计得到最优策略下对应的行为
a
k
∗
(
s
)
a_k^*(s)
ak∗(s)
第二步:值更新,同样的,通过给定的
v
k
v_k
vk 求得每个状态对应的
q
k
q_k
qk 再根据最优策略计算得到
v
k
+
1
v_{k+1}
vk+1

通过上面的讲解,我们得到下面的流程过程:

给出上述算法的伪代码,如下:

值迭代:案例
我们以一个例子加深理解。
r
边界
=
r
陷阱
=
−
1
,
r
终点
=
+
1
,
γ
=
0.9
r_{边界}=r_{陷阱}=-1,r_{终点}=+1,γ=0.9
r边界=r陷阱=−1,r终点=+1,γ=0.9

当
k
=
0
k=0
k=0


策略迭代
策略迭代分两步:策略评估
(
P
E
)
(PE)
(PE) 和策略优化
(
P
I
)
(PI)
(PI)。

求解
v
π
k
v_{πk}
vπk 有两种方法,第一种矩阵求解一般不用,主要是用第二种迭代的方法。

策略迭代具体步骤如下:


伪代码如下:

策略迭代:案例
同样,我们以一个例子加深理解。
r
边界
=
−
1
,
r
终点
=
+
1
,
γ
=
0.9
r_{边界}=-1,r_{终点}=+1,γ=0.9
r边界=−1,r终点=+1,γ=0.9,行为有:向左
a
l
a_l
al,向右
a
r
a_r
ar,原地
a
0
a0
a0



策略迭代:案例二

截断策略迭代算法
首先我们来比较一下值迭代与策略迭代的区别:


伪代码: