机器学习与深度学习——通过奇异值分解算法压缩图片

什么是奇异值分解？

奇异值分解（Singular Value Decomposition，SVD）是一种重要的线性代数方法，用于将一个矩阵分解成三个部分的乘积形式。它的应用非常广泛，包括数据降维、图像压缩、信号处理等领域。

对于一个 $m\times n$ 的实数矩阵 $A$ ，它的SVD分解可以表示为：

$\Sigma V^T$

其中， $U$ 和 $V$ 是正交矩阵， $\Sigma$ 是一个 $m\times n$ 的对角矩阵，且对角线上的元素 $\sigma_i$ 称为 $A$ 的奇异值（Singular Value）。具体来说，我们有以下步骤：

对矩阵 $AA^T$ 求特征值和特征向量，得到 $AA^T = U\Sigma^2U^T$ ，其中 $U$ 是由AA^{T的特征向量组成的正交矩阵，$\Sigma^2$是由AA}T的特征值组成的对角矩阵。
对矩阵 $A^TA$ 求特征值和特征向量，得到 $A^TA = V\Sigma^2V^T$ ，其中 $V$ 是由A^T A的特征向量组成的正交矩阵， $\Sigma^2$ 与上面一步相同。
将 $U$ 和 $V$ 中的列向量单位化。
令 $\Sigma$ 为 $\sqrt{\Sigma^2}$ 的矩阵，即对角线上的元素为 $\sigma_i$ ，其余为0。

最后得到的 $U$ 和 $V$ 满足 $UU^T=I$ 和 $VV^T=I$ ，即 $U$ 和 $V$ 是正交矩阵。这样，我们就将一个矩阵分解成了三个部分的乘积形式。更具体地说，我们可以将矩阵 $A$ 表示为：

$\Sigma V^T = \sum_{i=1}^{r}\sigma_iu_iv_i^T$

其中 $r$ 是矩阵 $A$ 的秩， $\sigma_i$ 是奇异值， $u_i$ 和 $v_i$ 分别是左奇异向量和右奇异向量，它们是对应于 $\sigma_i$ 的特征向量。奇异向量具有非常重要的性质，可以用于数据降维、图像压缩、信号处理等领域。

我们来做一个案列，感受一下奇异值分解算法。

目的

通过奇异值分解进行图片压缩，绘制出压缩后的图片和计算出压缩率

步骤

1、导入所需的库；
2、定义压缩函数 zip_img_by_svd
3、初始化压缩后的图片 zip_img 为全零数组
4、对每个通道进行 SVD 分解并进行归一化处理
5、将压缩后的近似矩阵乘以 255 并转换为 uint8 类型，并将原图像压缩成低维矩阵。
6、展示压缩前后的图像

代码：

#导入所需的库
import numpy as np
import matplotlib.pyplot as plt
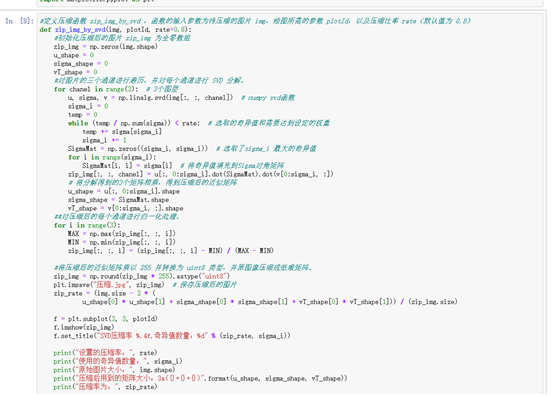
#定义压缩函数 zip_img_by_svd ，函数的输入参数为待压缩的图片 img，绘图所需的参数 plotId，以及压缩比率 rate（默认值为 0.8）
def zip_img_by_svd(img, plotId, rate=0.8):
#初始化压缩后的图片 zip_img 为全零数组，并初始化三个变量 u_shape、sigma_shape、vT_shape 为零。u_shape、sigma_shape、vT_shape 分别表示 u、sigma、vT 三个矩阵的形状
    zip_img = np.zeros(img.shape)
    u_shape = 0
    sigma_shape = 0
    vT_shape = 0
#对图片的三个通道进行遍历，并对每个通道进行 SVD 分解。然后通过奇异值数量，创建对应的 SigmaMat 对角矩阵，并将其填充为选取的奇异值。最后将三个矩阵相乘，得到压缩后的近似矩阵。
    for chanel in range(3):  # 3个图层
        u, sigma, v = np.linalg.svd(img[:, :, chanel])  # numpy svd函数
        sigma_i = 0
        temp = 0

        while (temp / np.sum(sigma)) < rate:  # 选取的奇异值和需要达到设定的权重
            temp += sigma[sigma_i]
            sigma_i += 1
        SigmaMat = np.zeros((sigma_i, sigma_i))  # 选取了sigma_i 最大的奇异值
        for i in range(sigma_i):
            SigmaMa
#对压缩后的每个通道进行归一化处理。
    for i in range(3):  # 对三个通道的矩阵数值进行归一化处理
        MAX = np.max(zip_img[:, :, i])
        MIN = np.min(zip_img[:, :, i])
        zip_img[:, :, i] = (zip_img[:, :, i] - MIN) / (MAX - MIN)
#将压缩后的近似矩阵乘以 255 并转换为 uint8 类型，并原图像压缩成低维矩阵。
## 保存压缩后的图片并输出相关压缩信息
plt.imsave("压缩.jpg", zip_img)  # 保存压缩后的图片
    zip_rate = (img.size - 3 * (
            u_shape[0] * u_shape[1] + sigma_shape[0] * sigma_shape[1] + vT_shape[0] * vT_shape[1])) / (zip_img.size)

    f = plt.subplot(3, 3, plotId)
    f.imshow(zip_img)
    f.set_title("SVD压缩率 %.4f,奇异值数量：%d" % (zip_rate, sigma_i))

    print("设置的压缩率：", rate)
    print("使用的奇异值数量：", sigma_i)
    print("原始图片大小：
#展示压缩前后的图像
if __name__ == '__main__':
    imgfile = "1.jpg"
    plt.figure(figsize=(12, 12))
    plt.rcParams['font.sans-serif'] = 'SimHei'  # 消除中文乱码
    img = plt.imread(imgfile)
    f1 = plt.subplot(331)  # 绘制子图，3行3列，3*3个子图，现在画第1幅
    f1.imshow(img)
    f1.set_title("原始图片")
    for i in range(8):  # 再画8个子图
        rate = (i + 1) / 10.0  # 压缩率 10% - 80%
        zip_img_by_svd(img, i + 2, rate)

效果图

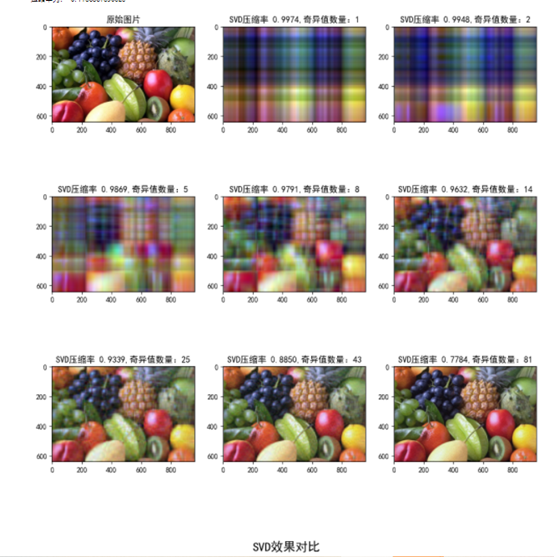
在这里插入图片描述

该代码主要分为两个部分：

zip_img_by_svd函数
这个函数接收待压缩的图片img，绘图所需的参数plotId以及压缩比率rate，然后对图片的三个通道进行遍历，并对每个通道进行奇异值分解（SVD）。然后通过设定的奇异值数量创建对应的SigmaMat对角矩阵，并将其填充为选取的奇异值。最后将三个矩阵相乘，得到压缩后的近似矩阵。

主函数
这个主函数首先读取指定路径下的原始图片，然后使用zip_img_by_svd函数对图片进行压缩，并展示压缩前后的图像。压缩率从10%变化到80%。

Σ是一个m×n的奇异值矩阵，对角线上的元素称为奇异值。SVD的一个重要应用是数据降维，即将高维数据压缩成低维数据，同时保留尽可能多的信息。在这个过程中，可以选择只保留最大的k个奇异值，从而得到一个k维的低维表示。

奇异值算法(Singular Value Algorithm,简称SVA)是一种用于求解矩阵特征值和特征向量的迭代算法。它的主要优点和缺点如下：

优点：