导入包

from utils import cos_sim, euclidean_dist

方法 EucSoftmax

变量

“”"Calculate cos distance loss.

Args:
    protos: protos vector in now episode (**class_size, hidden_size**)
    querys: queres vector to classify **(querys_len, hidden_size)**
    querys_y: corresponding y for query samples (**querys_len,** )
    t: (FloatTensor) temperature

Returns:
    return loss, neg dist (N*M)
"""

euclidean_dist(欧式距离）

欧氏距离也称为欧几里得距离，衡量得是多维空间中两个点之间绝对距离。

以古希腊数学家欧几里得命名的距离，也就是我们直观的两点之间直线最短的直线距离。

欧式距离的定义：是一个通常采用的距离定义，其是在$\ast \ast m$维空间中两个点之间的真实距离**。

在二维和三维空间中的欧氏距离就是两点之间的距离。二维的公式是:
$$d=\sqrt{(x_1-x_w{)}^2+(y_1-y_2{)}^2}$$

三维度的公式是:
$$d=\sqrt{(x_1-x_2{)}^2+（y_1-y_2{)}^2+(z1-z2{)}^2}$$

推广到n维空间欧氏距离公式为:
$$\sqrt{\sum _{i=1}^n(y_i-x_i{)}^2}$$

$$n维欧氏空间是一个点集.$$
实现方式：euclidean_dist(querys, protos)

F.cross_entropy

• F.cross_entropy(x,y)
    cross_entropy(x,y)是交叉熵损失函数，一般用于在全连接层之后，做loss的计算。

其中x是二维张量，是全连接层的输出；y是样本标签值。x[batch_size,type_num];y[batch_size]。

cross_entropy(x,y)计算结果是一个小数，表示loss的值。

损失函数-交叉熵损失函数公式

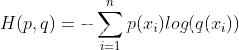
实现方式:
$$F.cros{s}_{e}ntropy(\ast \ast ne{g}_e{u}_{d}ists,query{s}_y\ast \ast )$$
返回值：loss_sfm, neg_eu_dists 损失值和欧氏距离的负数。

utils模块中的欧氏距离

def euclidean_dist(x, y):
    """Compute euclidean distance between two tensors

    Args:
        x: (Tensor) N x D
        y: (Tensor) M x D

    Returns:
        Euclidean distance of x and y, a float
    """
    flag = False
    if y is None:
        y = x
        flag = True
    if len(list(x.size())) == len(list(y.size())) == 1:
        return torch.pow(x - y, 2).sum()
    x_norm = (x ** 2).sum(1).view(-1, 1)
    y_t = torch.transpose(y, 0, 1)
    y_norm = (y ** 2).sum(1).view(1, -1)
    dist = x_norm + y_norm - 2.0 * torch.mm(x, y_t)
    # Ensure diagonal is zero if x=y
    if flag:
        dist = dist - torch.diag(dist.diag())
    return torch.clamp(dist, 0.0, np.inf)

方法CosT

"""Calculate cos distance loss.

Args:
    protos: protos vector in now episode (class_size, hidden_size)
    querys: queres vector to classify (querys_len, hidden_size)
    querys_y: corresponding y for query samples (querys_len, )
    t: (FloatTensor) temperature

Returns:
    return loss, neg dist (N*M)
"""

cos_sim（余弦相似度）

• 计算余弦相似度公式:
  $$cos=\frac{a\cdot b}{||a|||b|||}$$
  其中$a和b代表两个向量$，（注意：向量是在空间中具有大小和方向的量）

如果在二维空间中，余弦相似度的值通过以下公式计算:


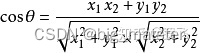
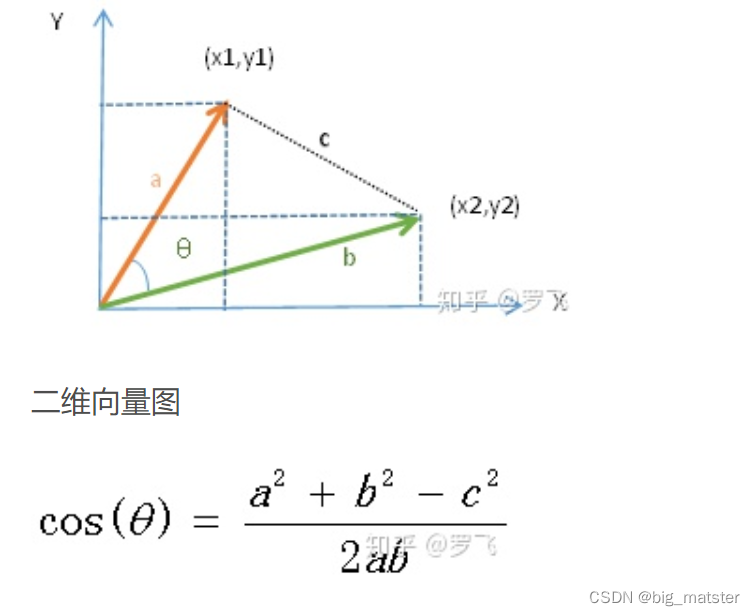
余弦定理:
二维空间下计算两个向量的余弦相似性公式是根据余弦定理推导出来的，请感兴趣的可以自己推演一下（可根据以上两图）。
如果假设空间是多维的，则余弦相似度公式可扩展如下图:

代码实现

• cos = cos_sim(querys, protos)
• t_cos = t * cos
• loss_cos = F.cross_entropy(t_cos, querys_y)
• return loss_cos, cos

余弦相似度代码为:

def cos_sim(x, y=None, eps=1e-8):
    """Cosine Similarity calculate. Add eps for numerical stability"""
    y = x if y is None else y
    if len(list(x.size())) == len(list(y.size())) == 1:
        return torch.nn.CosineSimilarity(dim=-1, eps=eps)(x, y)
    x_n, y_n = x.norm(dim=1)[:, None], y.norm(dim=1)[:, None]
    x_norm = x / torch.max(x_n, eps * torch.ones_like(x_n))
    y_norm = y / torch.max(y_n, eps * torch.ones_like(y_n))
    sim_mt = torch.mm(x_norm, y_norm.transpose(0, 1))
    return sim_mt

总结

先将代码复制下来，后续在继续深耕，各章节的代码及其模块实现方式都行的回事与打算。

EucTriplet

“”"Calculate cos distance loss.

Args:
    protos: protos vector in now episode (class_size, hidden_size)
    querys: queres vector to classify (querys_len, hidden_size)
    querys_y: corresponding y for query samples (querys_len, )
    t: (FloatTensor) temperature

Returns:
    return loss, neg dist (N*M)
"""

a = torch.arange(querys_size).to(device)

将所有最开始读取数据时候的$tensor$变量，copy一份到device所指定的GPU上去，之后的运算都在GPU上进行。
这句话需要写的次数等于需要保存GPU上的tensor变量的个数；一般情况下这些tensor变量都是最开始读数据时的tensor变量，后面衍生的变量自然也都在GPU上

代码展示

 device = protos.device
    querys_size = querys.size(0)
    a = torch.arange(querys_size).to(device)

    eu_dists = euclidean_dist(querys, protos)
    neg_eu_dists = -eu_dists

    masked_dists = eu_dists.clone()
    masked_dists[a, querys_y] = float('inf')

    neg_samples_dists = masked_dists.min(dim=-1)[0]
    pos_samples_dists = eu_dists[a, querys_y]

    loss_triplet = F.relu(pos_samples_dists - neg_samples_dists + 1.0).mean()
    return loss_triplet, neg_eu_dists

慢慢的将各种代码及包，全部搞定都行啦的里哟

F.relu

是一种人工神经网咯中常用的激活函数，通常意义下，其指的是：
数学中的斜坡函数: 即:
$$f(x)=max(0,x)$$
对应的函数图像如下所示:

• 会自己搞清楚，这篇论文的代码中如何使用激活函数。以及如何传惨的。
• 全部都将其搞定都行啦的样子与打算，慢慢的学会如何使用激活函数以及如何传参。
• 慢慢的研究一波都行啦的样子与打算。