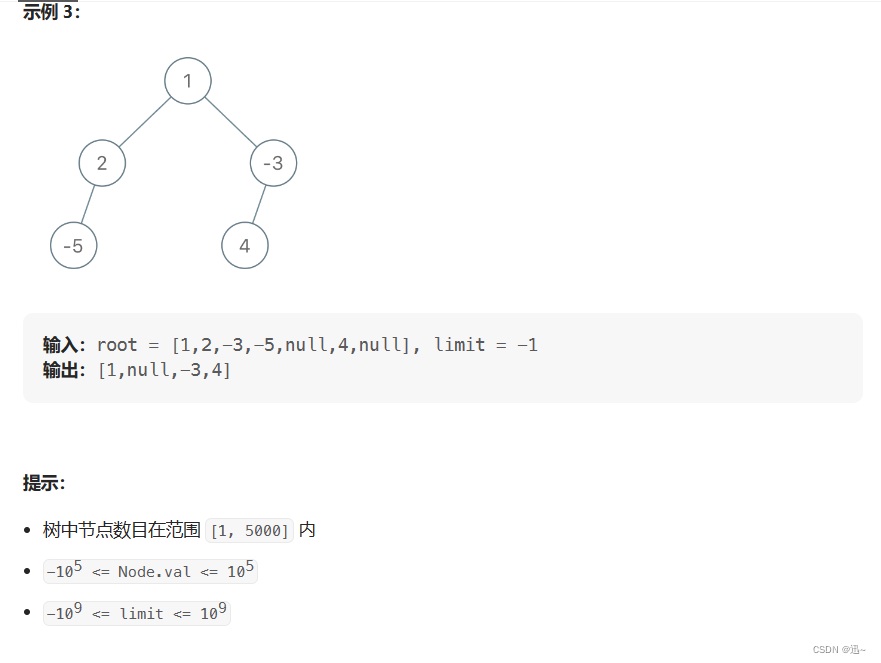
假设一个推销员问题由下图定义,用回溯法求解
从1号结点出发的相应最短巡回路径(每个顶点刚好到达一次)。若用bestL表示搜索过程中产生的当前最优解,剪枝函数 L 设计为:
L = 已走过的路径长度 + 当前结点相关的最短边 + 所有未访问结点的相关最短边之和。
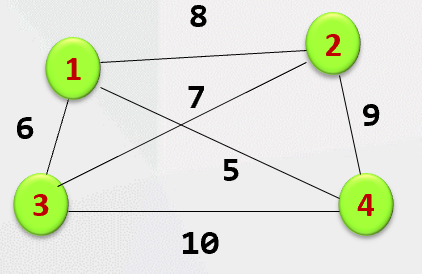
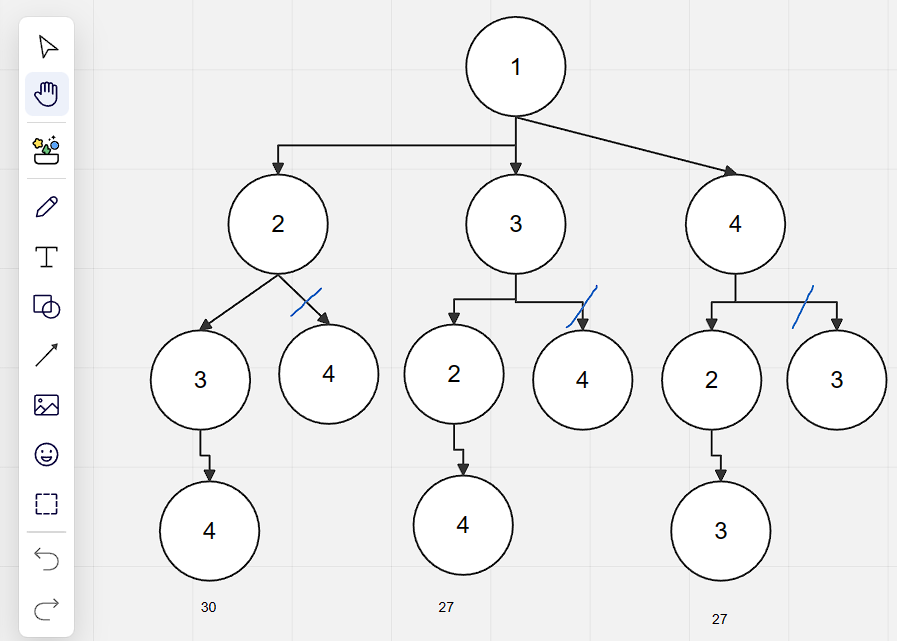
那么,走过结点:1->3->2时 ,bestL和 L的值分别是:A (如果先从2结点开始深度搜索的话)
A. 30和25
B. 30和28
C. 27和25
D. 27和28
回溯法是一种解决问题的递归算法。在回溯法中,我们尝试解决问题的每一部分,如果在解决当前部分时发现存在无法满足问题条件的情况,则回溯到上一步并尝试其他解决方案,直到问题被解决为止。在寻找最短路径时,我们可以将问题建模为一个图,其中每个点表示一个城市,每条边表示两个城市之间的距离。推销员需要从一个起点出发,经过所有城市后最终回到起点,所要走的路径就是我们需要寻找的最短路径。
对于剪枝函数L,它可以帮助我们在搜索过程中避免探索到不必要的路径,从而提高搜索效率。该函数的计算方式为:已走过的路径长度 + 当前结点相关的最短边 + 所有未访问结点的相关最短边之和。其中已走过的路径长度和当前结点相关的最短边都可以通过动态规划的方式进行计算,而所有未访问结点的相关最短边可以通过使用Dijkstra算法计算得出。
回溯法是一种搜索算法,可以在问题的解空间内找到满足特定限制条件的所有解。在搜索过程中,每次扩展一个子节点,会对当前状态进行判断,看看是否满足问题的限制条件。如果满足条件,则进行下一步扩展;如果不满足,则进行回溯,回退到上一个状态并重新选择其他路径继续搜索。
在回溯法中,当前最优解的定义是指:
在搜索过程中已经找到的所有解中,最接近目标解的解。
这个解不一定是全局最优解,但是对于当前搜索状态而言是最优的。
在搜索过程中,我们会不断尝试找到更加优秀的解,在找到更优解的同时也可能改变当前最优解的定义。
因此,在回溯法中,当前最优解是一个动态的概念。
具体来说,当我们在搜索过程中找到了一个新的解决方案时,我们会将其与当前最优解进行比较。如果新的解决方案更优,则更新当前最优解;否则,我们继续搜索其他可能的解决方案。
在某些情况下,我们可以使用剪枝技术来提高回溯法的效率。例如,在搜索过程中,如果当前正在搜索的解已经比当前最优解要差,那么我们可以直接跳过这个解,从而避免不必要的搜索。
回溯算法的基本思想是:从一条路往前走,能进则进,不能进则退回来,换一条路再试。