作者：小迅
链接：https://leetcode.cn/problems/insufficient-nodes-in-root-to-leaf-paths/solutions/2279048/di-gui-zhu-shi-chao-ji-xiang-xi-by-xun-g-7rfd/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

题目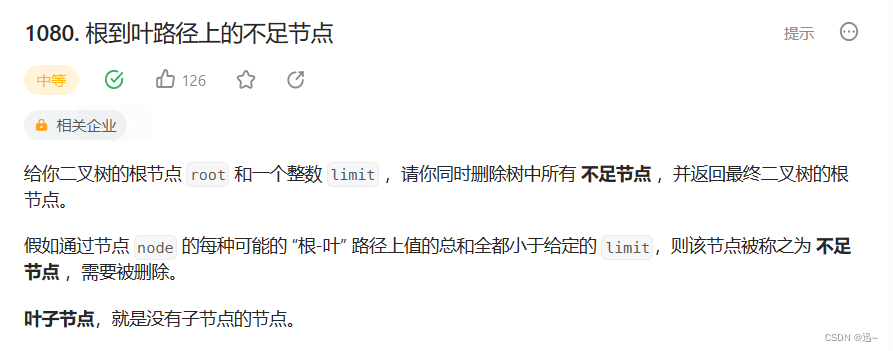

 

示例

 

 

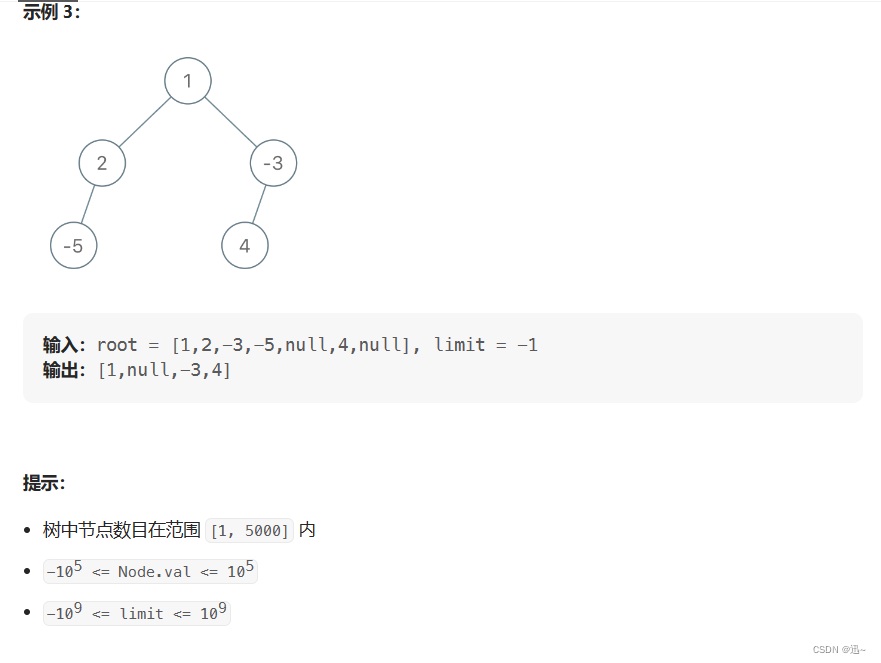
思路

 

给定一个二叉树，删除 “根-叶” 路径上值的总和小于 limit 的节点

任何一条有效路径的起点都是根节点，而终点都是叶子节点，中间节点值的累和就是当前路径的有效值，如果有效值小于limit，则将该路径的叶子节点删除，那么删除的叶子节点的父节点就将成为当前路径的尾子节点。

• 如果该节点还有子节点的话，该路径就相当于该道了，就需要重复之前的判断，看看是否需要删除子节点；
• 如果该节点没有子节点的话，就说明该节点为当前路径的叶子节点，需要删除，因为当前路径累和没有大于limit。

所以当前节点是否要删除取决于当前节点的子节点

• 如果当前节点左右子节点都会被删除，那么当前节点也要被删除
• 如果当前节点左右子节点有一个没有被删除，那么当前节点就不会被删除

综上本题就是二叉树的后序遍历，先处理子节点，再处理根节点。

注：当有需要单调处理头节点时，常用的做法是申请一个哨兵节点，指向头节点，可以避免单调处理头节点

代码注释超级详细

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
#define MAX(a, b) ((a) > (b) ? (a) : (b))

void delete(struct TreeNode* root)//删除节点
{
    if (root == NULL) return;//已经为空，则结束
    delete(root->left);//递归删除
    delete(root->right);
    root->left = NULL;//删除本节点
    root->right = NULL;
    free(root);
    return;
}

int dfs(struct TreeNode* root, int limit, int val)
{
    if (root->left == NULL && root->right == NULL) {//叶子节点
        return (root->val + val) < limit ? 1 : 0;//整个路径有效值小于limit
    }
    int left = 1, right = 1;// 1 表示需要删除
    //后序遍历
    if (root->left) left = dfs(root->left, limit, root->val+val);
    if (root->right) right = dfs(root->right, limit, root->val+val);
    if (left) {//左节点需要删除
        delete(root->left);
        root->left = NULL;
    }
    if (right) {//有节点需要删除
        delete(root->right);
        root->right = NULL;  
    }
    return left && right;//如果子节点都删除，自己也没必要活着，此路不通
}

struct TreeNode* sufficientSubset(struct TreeNode* root, int limit){
    struct TreeNode* head = malloc(sizeof(struct TreeNode));
    head->val = 0;
    head->left = root;
    head->right = NULL;//构造哨兵
    dfs(head, limit, 0);
    root = head->left;
    head->left = NULL;
    free(head);//销毁哨兵
    return root;
}

作者：小迅
链接：https://leetcode.cn/problems/insufficient-nodes-in-root-to-leaf-paths/solutions/2279048/di-gui-zhu-shi-chao-ji-xiang-xi-by-xun-g-7rfd/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。