一、题目描述

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

进阶：如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。

二、代码实现

方法一：暴力法

解题思路

  枚举数组 nums 中的每个下标作为子数组的开始下标，对于每个开始下标 i，需要找到大于或等于 i 的最小下标 j，使得从 nums[i] 到 nums[j] 的元素和大于或等于 s，并更新子数组的最小长度（此时子数组的长度是 j−i+1）。

代码实现

func minSubArrayLen1(target int, nums []int) int {
	minLen := math.MaxInt
	for i := 0; i < len(nums); i++ {
		sum := 0
		for j := i; j < len(nums); j++ {
			sum += nums[j]
			if sum >= target {
				minLen = min(minLen, j-i+1)
				break
			}
		}
	}
	if minLen == math.MaxInt {
		return 0
	}
	return minLen
}
func min(x, y int) int {
	if x < y {
		return x
	}
	return y
}

复杂度分析

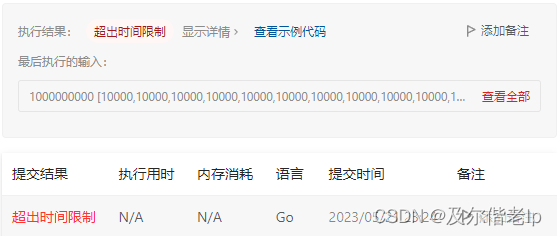
• 时间复杂度：O(n^2 )，其中 n 是数组的长度。需要遍历每个下标作为子数组的开始下标，对于每个开始下标，需要遍历其后面的下标得到长度最小的子数组。
• 空间复杂度：O(1)。

方法二：滑动窗口 + 双指针

解题思路

  定义两个指针 left 和 right 分别表示子数组（滑动窗口）的开始位置和结束位置，维护变量 sum 存储子数组中的元素和（即从 nums[left] 到 nums[right] 的元素和）。

  初始状态下，left 和 right 都指向下标 0，sum 的值为 0。每一轮迭代，将 nums[right] 加到 sum，如果 sum≥target，则更新子数组的最小长度（此时子数组的长度是 right−left+1），然后将 nums[left] 从 sum 中减去并将 left 右移，直到 sum<target，在此过程中同样更新子数组的最小长度。在每一轮迭代的最后，将 right 右移。

代码实现

func minSubArrayLen(target int, nums []int) int {
	left, right := 0, 0
	minLen := math.MaxInt
	sum := 0
	for right < len(nums) {
		sum += nums[right]
		for sum >= target {
			minLen = min(minLen, right-left+1)
			sum -= nums[left]
			left++
		}
		right++
	}
	if minLen == math.MaxInt {
		return 0
	}
	return minLen
}
func min(x, y int) int {
	if x < y {
		return x
	}
	return y
}

复杂度分析

• 时间复杂度：O(n)，其中 n 是数组的长度。指针 left 和 right 最多各移动 n 次。

• 空间复杂度：O(1)。

方法三：前缀和 + 二分查找

解题思路

  方法一采用暴力枚举，时间复杂度是 O(n^2 )，因为在确定每个子数组的开始下标后，找到长度最小的子数组需要 O(n) 的时间。如果使用二分查找，则可以将时间优化到 O(logn)。

  每个下标开始的这个遍历过程计算了很多重复的区间，比如1，2，3，4 。以1为下标时计算了+2、+3、+4 ; 以2为下标时计算了+3、+4，像这种避免区间和重复计算的优化方法，我们想到了前缀和，可以O(1)时间迅速得到任意区间的和。

  然后 ，我们可以很容易得改良问题为，求s[j] - s[i] >=target ，可是这种做法如果不加改变，就是在前缀和数组上进行类似方法一的暴力枚举，枚举每一个 i 后面的下标 j 。我们发现稍作变化，像这种线性的求值问题，联合二分查找可以做到 求 s[j] >=s[i]+target，将时间优化到 O(logn)。

代码实现

func minSubArrayLen(target int, nums []int) int {
	ans := math.MaxInt32
	sums := make([]int, 1)
	for i := 1; i <= len(nums); i++ {
		sums = append(sums, sums[i-1]+nums[i-1])
	}
	for i := 1; i <= len(nums); i++ {
		num := target + sums[i-1]
		bound := sort.SearchInts(sums, num)
		if bound <= len(nums) {
			ans = min(ans, bound-(i-1))
		}
	}
	if ans == math.MaxInt32 {
		return 0
	}
	return ans
}
func min(x, y int) int {
	if x < y {
		return x
	}
	return y
}

复杂度分析

• 时间复杂度：O(nlogn)，其中 n 是数组的长度。需要遍历每个下标作为子数组的开始下标，遍历的时间复杂度是 O(n)，对于每个开始下标，需要通过二分查找得到长度最小的子数组，二分查找得时间复杂度是 O(logn)，因此总时间复杂度是 O(nlogn)。

• 空间复杂度：O(n)，其中 n 是数组的长度。额外创建数组 sums 存储前缀和。