目录

8.1.B树

8.1.1.概述

8.1.2.完整建树过程

8.2.B+树

---

8.1.B树

8.1.1.概述

B树存在的意义：

二叉树在存储数据时可能出现向一边倾斜导致查询效率降低的情况，为了防止二叉树的倾斜，出现了平衡二叉树，通过旋转的方式保证二叉树的平衡。但是就算是保持绝对的平衡，在面对要存储的数量量级够大的时候也会出现树的高度整体偏高的问题，树的高度过高，即使是使用了二分查找，依然会出现查找效率变低的情况。尤其是磁盘查找数据本身是个机械完成的动作，这一动作本身就十分耗时。因此需要一种能进行二分查找缩短查找时间，能存储大量数据后树高也不会过高的树形结构，这就是B树。

B树的概念：

B树又称为多路平衡查找树，满足以下规则：

• 基本结构
  • 每个结点可以存放多个数据，每个结点的数据实体处理存放数据外有左右指针指向自己的子结点，也就是说当前结点存放n个数据的话，它最多能有n-1个指针指向自己的子结点。
• B树的阶数
  • 阶数，代表单个节点最多有多少个查找路径，也就是单结点的指针数量，当阶数=2时，这棵B树就是二叉树。
• 排序方式
  • 单结点内部按照升序排列。结点之间，左结点<根结点<右结点
• 子结点数
  • 非叶节点的子节点数>1，且<=M ，且M>=2，空树除外
• 单结点的数据存放上限
  • 大于等于ceil(阶数/2)-1个且小于等于阶数-1个，ceil()是个朝正无穷方向取整的函数 如ceil(1.1)结果为2。

以下展示一个B树的示例，省略号表示为了节约作图空间没画出来但是存在的结点：

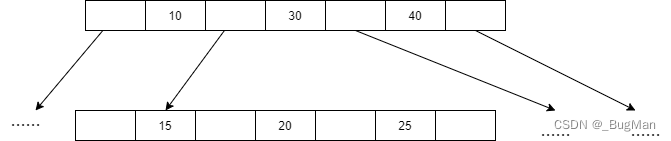
B树的缺点：

不适合范围查找，例如我们要查找上面这棵B树里>5的数据，那么要在找到15后还要继续查找30右边的指针，40右边的指针......可以看到需要进行很繁复的遍历。

8.1.2.完整建树过程

3、8、31、11、23、29、50、28  构建一个5阶B树。

5阶B树，因此每个节点有4个关键字，5个分支。

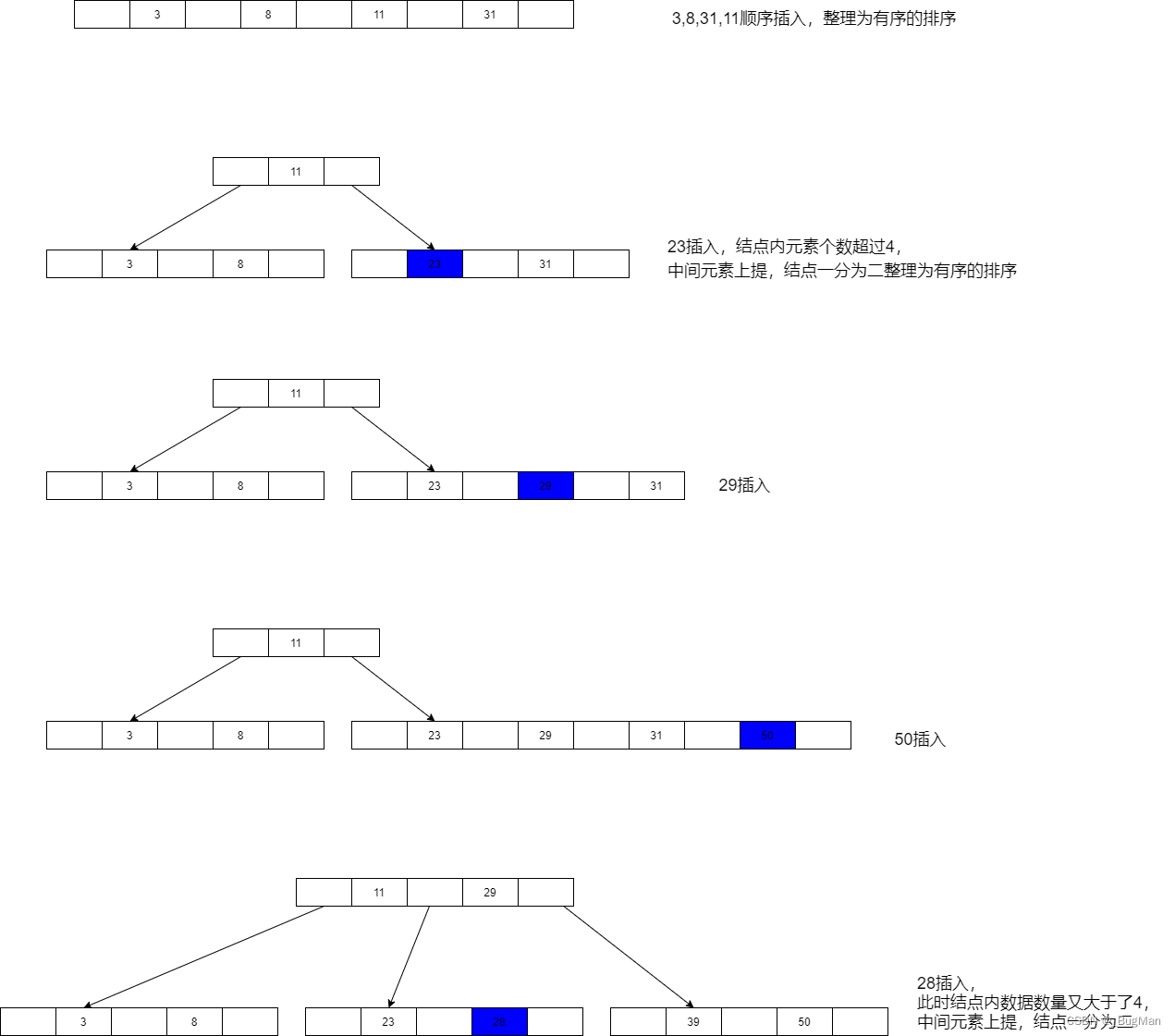
8.2.B+树

因为B树对范围查询效果不好，于是出现了对于范围查询有较好支持的B+树。

B+树其实就是专门为了更好的支持范围查询，微调了一下B树的结构。

思路：

• 每个分支的叶子结点上挂载这路分支上的所有数据。
• 这样可以保证树的最后一层上有整棵树的所有数据，并且在叶子结点层级上会呈现出数据均匀分块的效果。
• 将叶子结点用双向指针连起来（图中有误）。
• 这样进行范围查找的时候直接走到叶子结点层，然后在沿着指针查找即可。优化了B树的范围查找能力。

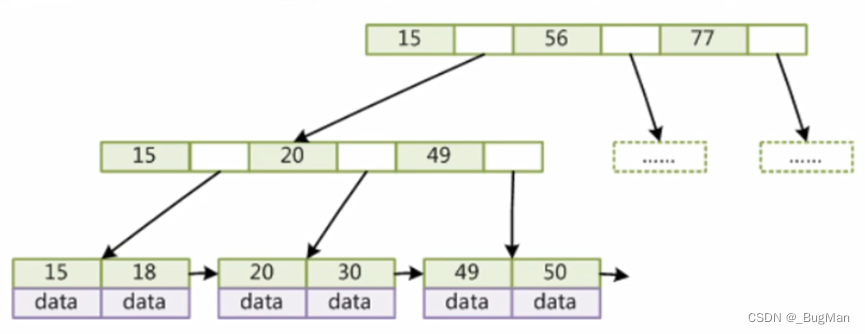
可以看到B树和B+树各有优缺：

存放同样的数据，B树的内存开销要低于B+树，因为B+树在叶结点挂了路径上的所有数据，相当于把数据存了两份。但是B+树的范围查询效率更好。