F检验是一种重要的医学统计方法,常用于检验两个或多个样本的方差是否相等,也被称为方差齐性检验。方差齐性检验是医学研究中的基本方法,因为许多重要的统计分析都要求样本方差相等,如方差分析、t检验等。以下将介绍F检验的基本原理、假设检验、计算公式以及在医学研究中如何使用F检验。
1、检验的基本原理
F检验是一种比较两个或多个样本的方差大小来判断它们是否相等的统计方法。具体而言,F检验是通过计算F值来判断两个或多个样本的方差是否相等,F值越大表示两个样本的方差差异越大,F值越小表示两个样本的方差差异越小,如果F值接近1,则表示两个样本的方差相等。
2、F检验的假设检验
在F检验中,需要建立原假设和备择假设,以判断两个或多个样本的方差是否相等。通常来说,我们假设两个或多个样本的方差相等,即:
H0: σ1^2=σ2^2=…=σk^2
H1: 至少有一组样本的方差与其他样本不相等。
其中,k为样本数。
3、F检验的计算公式

其中
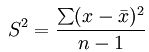
然后计算的F值与查表得到的F表值比较,F值越大,p值越小,如果
F < F表 表明两组数据没有显著差异;
F ≥ F表 表明两组数据存在显著差异。
4、F检验实例
比较不同年龄组之间患糖尿病的风险为例。
假设有两组数据,一组为50岁以下的人群,另一组为50岁以上的人群,随机选取了各自10个样本。用F检验判断两组人群患糖尿病的风险的方差是否不等。
50岁以下人群:2, 3, 5, 3, 4, 6, 5, 7, 6, 3
50岁以上人群:8, 6, 9, 7, 10, 8, 11, 12, 9, 10
下面进行F检验,检验两组样本的方差是否相等。
H0: σ1^2=σ2^2,即两组样本的方差相等。
H1: σ1^2≠σ2^2,即两组样本的方差不相等。
计算50岁以下人群的方差和50岁以上人群的方差:
| 年龄组 | 样本数 | 平均数 | 方差 |
|---|---|---|---|
| 50岁以下人群 | 10 | 4.4 | 2.71 |
| 50岁以上人群 | 10 | 9.0 | 3.33 |
F = (3.33 /2.71) =1.23
使用α=0.1的置信水平进行双尾检验,自由度分别为n1-1=9和n2-1=9,根据F分布表,可以得到临界值为Fα/2(9, 9)=3.18。
由于计算得到的F值(1.23)小于临界值(3.18),因此不能拒绝H0。即认为两组样本的方差相等。