hot100题

560. 和为 K 的子数组

560. 和为 K 的子数组

• 先暴力，过了再说

public int subarraySum(int[] nums, int k) {
    int ans = 0;
    for (int i = 0; i < nums.length; i++) {
        int sum = 0;
        for (int j = i; j < nums.length; j++) {
            sum += nums[j];
            if(sum==k) ans++;
        }
    }
    return ans;
}

想想之前遍历树时遇到过这个问题，当时用前缀和+Map做得，飞快呀，这里不也可以么

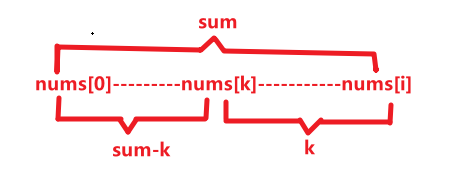
果然可以，快了不是一点点啊

public int subarraySum(int[] nums, int k) {
    HashMap<Integer, Integer> hash = new HashMap<>();
    hash.put(0,1);//初始化 很重要
    int ans = 0,sum=0;
    for (int i = 0; i < nums.length; i++) {
        sum += nums[i];
        ans += hash.getOrDefault(sum-k,0);// root-A-current   root~current=sum   root~A=sum-k 那么 A~current一定是k
        hash.put(sum,hash.getOrDefault(sum,0)+1);
    }
    return ans;
}

这么写，会快2~3ms

public int subarraySum(int[] nums, int k) {
    HashMap<Integer, Integer> hash = new HashMap<>();
    hash.put(0,1);//初始化 很重要
    int ans = 0,sum=0;
    for (int num : nums) {
        sum += num;
        if(hash.containsKey(sum-k))  ans += hash.get(sum - k);
        if(hash.containsKey(sum)){
            hash.put(sum,hash.get(sum)+1);
        }else {
            hash.put(sum,1);
        }
    }
    return ans;
}

581. 最短无序连续子数组 ▲

581. 最短无序连续子数组

• 老规矩，先暴力通过再说

public int findUnsortedSubarray(int[] nums) {
    int l=-1,r=-1;
    for (int i = 0; i < nums.length; i++) {
        for (int j = i + 1; j < nums.length; j++) {
            if (nums[j] < nums[i]){//正序遍历 第一个不满足升序的
                l = i;
                break;
            }
        }
        if(l!=-1) break;
    }

    for (int i = nums.length - 1; i >= 0; i--) {
        for (int j = i-1; j >= 0; j--) {
            if (nums[j] > nums[i]){//逆序遍历 第一个不满足降序的
                r = i;
                break;
            }
        }
        if(r!=-1) break;
    }
    return l<r?r-l+1:0;
}

或者排序后比较前最长前缀和最长后缀

public int findUnsortedSubarray(int[] nums) {
    HashMap<Integer, Integer> map = new HashMap<>();
    int[] sort = Arrays.copyOf(nums, nums.length);
    Arrays.sort(sort);
    int l=0,r=nums.length-1;
    while (l<nums.length&&nums[l]==sort[l]) l++;
    while (r>0&&nums[r]==sort[r]) r--;
    return l<r?r-l+1:0;
}

竟然才7ms,也挺快的呀

• 方法1想法不错 但其实实现没那么麻烦

left应该小于右边所有元素 为何非要从前往后遍历呢，从后往前遍历 其实一趟就够了呀
同样right是后面都比它大 也可以从前往后一趟遍历

public int findUnsortedSubarray(int[] nums) {
    // 想法不错 但其实实现没那么麻烦
    // left应该小于右边所有元素 为何非要从前往后遍历呢，从后往前遍历 其实一趟就够了呀
    int min = Integer.MAX_VALUE, minI = -1;
    for (int i = nums.length-1; i >= 0; i--) {
        if(nums[i]>min) {
            minI=i;
        }else {
            min = nums[i];
        }
    }

    // 同样right是后面都比它大 也可以从前往后一趟遍历
    int max = Integer.MIN_VALUE, maxI=-2;
    for (int i = 0; i < nums.length; i++) {
        if(nums[i]<max) {
            maxI = i;
        }else {
            max = nums[i];
        }
    }

    return minI<maxI?maxI-minI+1:0;
}

当然两次遍历可以优化为1次遍历

public int findUnsortedSubarray(int[] nums) {
    // 想法不错 但其实实现没那么麻烦
    // left应该小于右边所有元素 为何非要从前往后遍历呢，从后往前遍历 其实一趟就够了呀   right也是
    int min = Integer.MAX_VALUE, minI = -1;
    int max = Integer.MIN_VALUE, maxI = -2;
    int n = nums.length;
    for (int i = n - 1; i >= 0; i--) {
        if (nums[i] > min) minI = i;
        else min = nums[i];

        if (nums[n - 1 - i] < max) maxI = n - 1 - i;
        else max = nums[n - 1 - i];
    }
    return minI < maxI ? maxI - minI + 1 : 0;
}

617. 合并二叉树

617. 合并二叉树

同步遍历，但是得先验证，后验的话root=null->root=new TreeNode() 连不起来

0ms 时间效率还不错

public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
    if(root1==null) return root2;
    if(root2==null) return root1;//开始根就为null的特判

    root1.val += root2.val;

    //System.out.printf("(%d %d)", root1 == null ? -1 : root1.val, root2 == null ? -1 : root2.val);

    if (root1.left != null || root2.left != null) {
        if (root1.left == null) root1.left = new TreeNode(0);
        else if (root2.left == null) root2.left = new TreeNode(0);
        mergeTrees(root1.left, root2.left);
    }

    if (root1.right != null || root2.right != null) {
        if (root1.right == null) root1.right = new TreeNode(0);
        else if (root2.right == null) root2.right = new TreeNode(0);
        mergeTrees(root1.right, root2.right);
    }

    return root1;
}

• 其实宏观层面看递归，巧用返回值，代码非常优美

public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
    if(root1==null) return root2;
    if(root2==null) return root1;

    TreeNode merge = new TreeNode(root1.val+root2.val);
    merge.left = mergeTrees(root1.left,root2.left);
    merge.right = mergeTrees(root1.right,root2.right);

    return merge;
}