目录
1.问题描述
2 GAMS代码要点
2.1 代码编写要点
2.2 案例源码
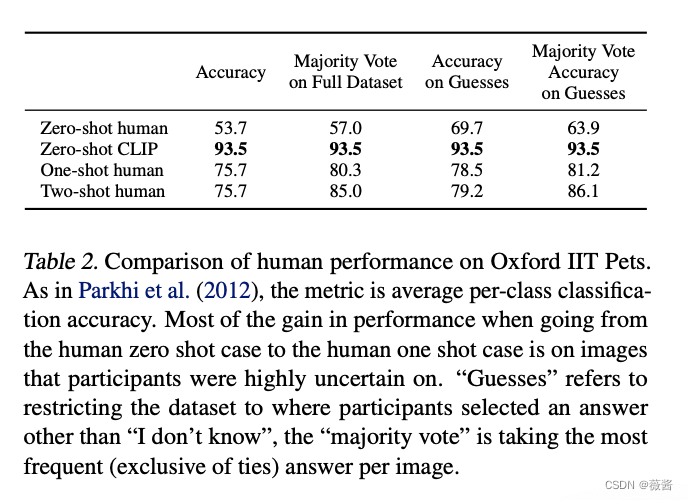
2.3 计算结果及报告解
1.问题描述
首先给出一个基本线性规划问题的计算案例
subject to:
2 GAMS代码要点
2.1 代码编写要点
- 使用 * 表示注释文本
- 定义变量
- Positive Variable 表示定义非负变量
- Negative Variable 表示定义非正变量
- Binary Variable 表示定义二进制决策变量
- Integer Variable 表示定义整数决策变量
- Free Variable 表示定义正决策变量
- 定义约束条件:
- 使用 Equations 关键字,首先给出约束名称列表,各约束以逗号分隔,以分号结尾
- 使用 =E= 、 =L= 和 =G= 分别表示 等式约束、小于等于约束、大于等于约束
- 目标函数在等式中以额外的等式表示,等式一侧为目标自由变量,另一侧为目标表达式
- 模型构建
- 使用 Model 关键字开头,紧跟着模型的名字、模型包含的约束和目标等式
- 使用 Options关键字定义模型类型和求解器
- 求解模型
- 使用 Solve 关键字开头的语句
- 表达式为: Solve 模型名 using 模型类型 优化目标类型 目标变量
- 结果展示
- 使用Display关键字开头的语句
2.2 案例源码
* max: 30 x1 + 100 x2 - 50 x3
* subject to
* x1 + x2 + x3 <= 7
* 4 x1 + 2x2 = 40
* 10x1 + + x3 >= 30
* x1 >=0, x2 \in R, x3 <= 0
Positive Variable x1;
Free Variable x2, z;
Negative Variable x3;
Equations
ConLE, ConEq, ConGE, Obj;
ConLE.. x1 + x2 + x3 =L= 7;
ConEq.. 4*x1 + 2*x2 =E= 40;
ConGE.. 10*x1 + x3 =G= 30;
Obj.. z =E= 30*x1 + 100*x2 - 50*x3;
Model SampleProblem1 /ConLE, ConEq, ConGE, Obj/
Options LP = Cplex;
Solve SampleProblem1 using LP maximizing z;
Display x1.L, x2.L, x3.L, z.L;
2.3 计算结果及报告解读
计算结果中包含以下几个项目:

其含义如下:
- 回显打印,将你输入的模型在报告中重新显示一边
- Equation Listing 表示模型中用到的所有约束及目标函数
- Column Listing 展示决策变量在不同等式中的系数
- MODEL STATISTICS 统计模型中拥有的等式数目、变量数目;模型生成和执行的耗时信息
- Solution Report 解的基本信息,包含模型的类型、求解器、状态、目标值等信息
- Display 部分给出模型的最优值和最优解信息
VARIABLE x1.L = 3.909
VARIABLE x2.L = 12.182
VARIABLE x3.L = -9.091
VARIABLE z.L = 1790.000
同时cong解的信息中,我们还可以看到我们用的这个案例有一个极方向:
Model has an unbounded ray.
**** ERRORS/WARNINGS IN EQUATION ConLE
1 error(s): Unbounded equation (slack variable)LOWER LEVEL UPPER MARGINAL
---- EQU ConLE -INF 7.0000 7.0000 -30.0000 UNBND
---- EQU ConEq 40.0000 40.0000 40.0000 65.0000
---- EQU ConGE 30.0000 30.0000 +INF -20.0000
---- EQU Obj . . . 1.0000LOWER LEVEL UPPER MARGINAL
---- VAR x1 . 3.9091 +INF .
---- VAR x2 -INF 12.1818 +INF .
---- VAR z -INF 1790.0000 +INF .
---- VAR x3 -INF -9.0909 . .
**** REPORT SUMMARY : 0 NONOPT
0 INFEASIBLE
1 UNBOUNDED (UNBND)