Trie
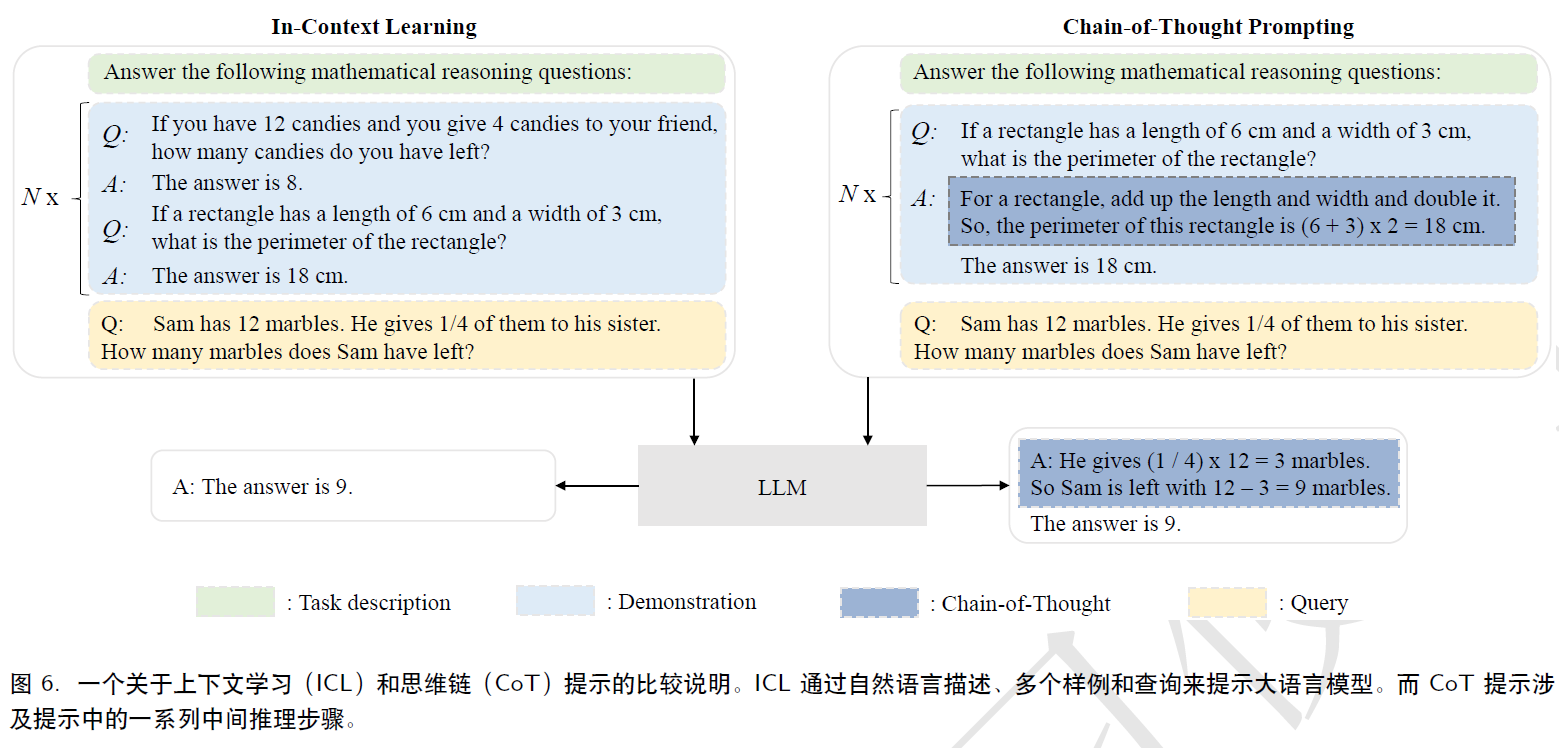
Trie,也称为字典树或前缀树,是一种用于高效存储和检索字符串的树形数据结构。它的主要特点是利用字符串的公共前缀来减少存储空间和提高查询效率。下面是对 Trie 的常见操作的介绍:
插入(Insertion):将一个字符串插入到 Trie 中。从根节点开始,逐个字符检查字符串,并根据字符是否存在于当前节点的子节点中进行相应的操作。如果字符不存在,则创建一个新的节点并将其链接到当前节点的子节点上。
删除(Deletion):从 Trie 中删除一个字符串。与插入操作类似,逐个字符检查字符串并找到对应的节点。在删除操作中,我们需要注意保留 Trie 的结构完整性,即如果删除一个节点后,它的父节点没有其他子节点且不代表其他字符串的前缀,则需要将该父节点也删除。
查询(Search):在 Trie 中搜索一个字符串。从根节点开始,逐个字符检查字符串。如果所有字符都存在于 Trie 中并且最后一个字符对应的节点标记为字符串的结尾,则说明字符串存在于 Trie 中。
前缀搜索(Prefix Search):在 Trie 中搜索具有指定前缀的所有字符串。从根节点开始,逐个字符检查前缀。如果前缀的所有字符存在于 Trie 中,可以通过遍历 Trie 的子节点来找到所有以该前缀开头的字符串。
统计前缀数量(Count Prefixes):统计以指定前缀开头的字符串的数量。与前缀搜索类似,从根节点开始,逐个字符检查前缀,并跟踪到达前缀末尾的节点。然后可以遍历该节点的子节点,统计以该前缀开头的字符串的数量。
这些操作是 Trie 的基本操作,通过利用 Trie 数据结构的特点,我们可以在常数时间内执行这些操作,从而实现高效的字符串存储和检索。在实际应用中,Trie 在单词查找、前缀匹配、自动补全、拼写检查等领域都有广泛的应用。
例题 1:
在给定的 N个整数 A1,A2……AN中选出两个进行 xor(异或)运算,得到的结果最大是多少?
输入格式 第一行输入一个整数 N 第二行输入 N 个整数 A1~AN
输出格式 输出一个整数表示答案。
数据范围 1≤N≤105 0≤Ai<231
输入样例: 3 1 2 3
输出样例: 3
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int tr[N * 30][2],idx;
int n;
int a[N];
void insert(int v)
{
int p = 0;
for(int i = 31; ~i; i --)
{
int c = v >> i & 1;
if(tr[p][c] == 0) tr[p][c] = ++idx;
p = tr[p][c];
}
}
int query(int v)
{
int p = 0;
int ans = 0;
for(int i = 31; ~i; i --)
{
int c = v >> i & 1;
if(tr[p][!c])
{
ans += (1 << i);
p = tr[p][!c];
}
else p = tr[p][c];
}
return ans;
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++ )
{
cin >> a[i];
insert(a[i]);
}
int ans = -1 << 30;
for(int i = 1; i <= n; i ++ )
{
ans = max(ans ,query(a[i]));
}
cout << ans;
return 0;
}
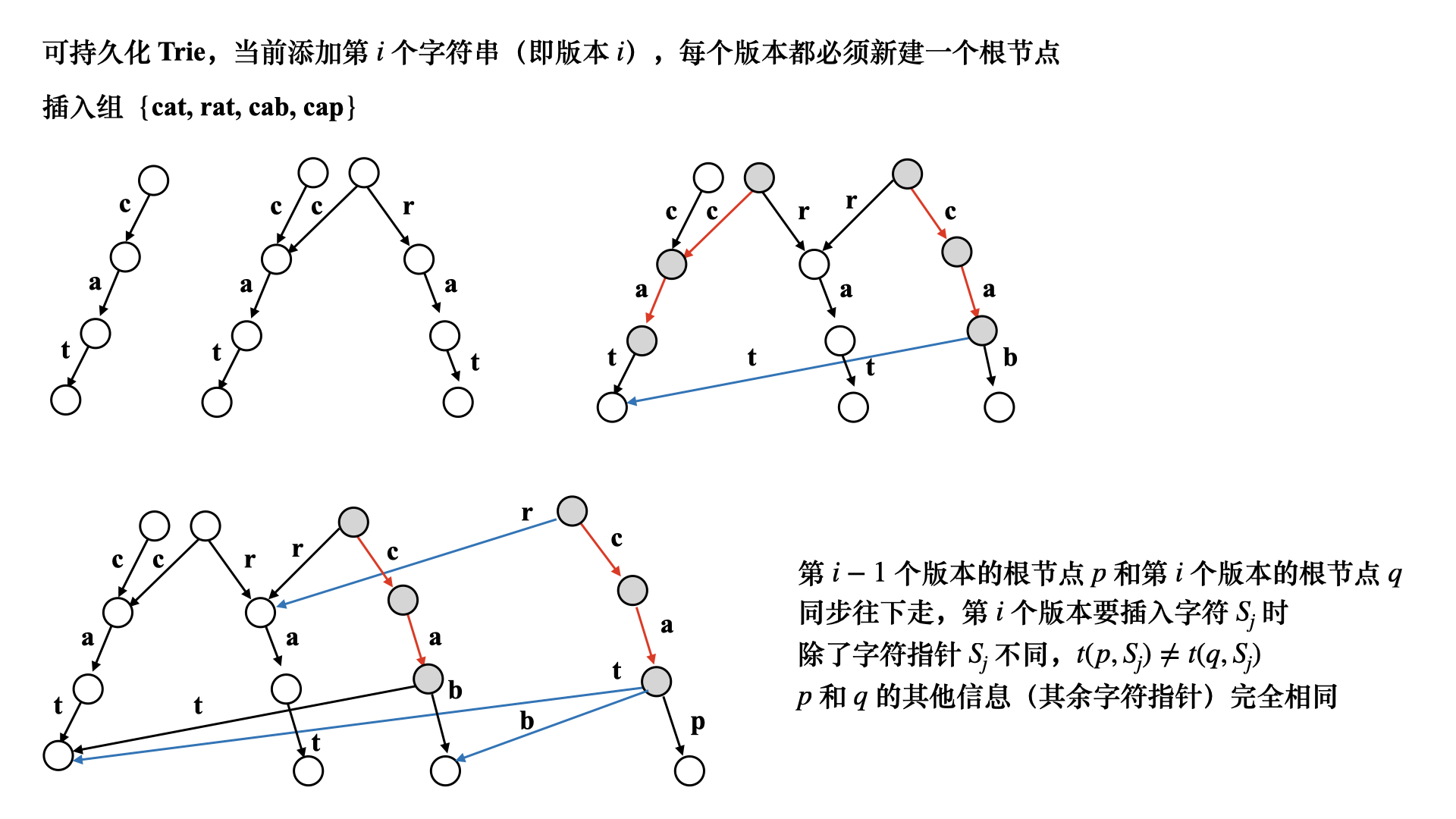
可持久化Trie
可持久化 Trie 是一种基于 Trie 数据结构的扩展,它允许我们在 Trie 中保留历史版本,而不仅仅是对当前状态的操作。可持久化 Trie 可以有效地支持在不同版本之间进行查询和修改操作。
在传统的 Trie 数据结构中,每次插入或删除一个单词时,会直接在当前的 Trie 上进行操作,这导致了无法回溯到之前的状态。但是,在可持久化 Trie 中,我们会使用一种持久化的方式来记录 Trie 的每个版本,并保留了每个版本的所有修改操作。
在可持久化 Trie 中,每个节点都包含一个指向子节点的数组或指针,并且每个节点还记录了一个版本号。当需要进行插入或删除操作时,我们会创建一个新的节点来表示新的版本,并将变化应用到新的节点上,同时保留旧版本的节点不变。
通过这种方式,可持久化 Trie 实现了对历史版本的查询能力。我们可以根据需要回溯到任意一个版本,并进行相应的查询操作,而不会影响其他版本的数据。
可持久化 Trie 在许多应用中都具有重要的作用,例如字符串的版本管理、历史记录、文本编辑器的撤销/重做等。它提供了一种高效、可靠的方法来处理需要对数据结构进行时间旅行的场景。
需要注意的是,可持久化 Trie 在时间和空间上都会有一定的开销,因为每个版本都需要额外的空间来存储节点的副本。因此,在实际应用中,我们需要根据具体需求权衡时间和空间的利弊,选择是否使用可持久化 Trie。
总结起来,可持久化 Trie 是一种可以保留历史版本并支持回溯的 Trie 数据结构扩展,它提供了对历史状态的查询能力,适用于许多需要对数据结构进行时间旅行的应用场景。
参考:AcWing 256. 最大异或和 - AcWing
例题:
给定一个非负整数序列 a,初始长度为 N。有 M 个操作,有以下两种操作类型: A x:添加操作,表示在序列末尾添加一个数 x,序列的长度 N 增大 1 Q l r x:询问操作,你需要找到一个位置 p,满足 l≤p≤r,使得:a[p] xor a[p+1] xor … xor a[N] xor x 最大,输出这个最大值。
输入格式 第一行包含两个整数 N,M,含义如问题描述所示。 第二行包含 N 个非负整数,表示初始的序列 A 接下来 M行,每行描述一个操作,格式如题面所述。
输出格式 每个询问操作输出一个整数,表示询问的答案。 每个答案占一行。
数据范围 N,M≤3×105,0≤a[i]≤107
解题思路:
1.根据xor运算的性质,可以发现,用类似加法前缀和的方式维护异或和S数组同样成立
2.原问题转化为 已知整数val = s[N] xor x,求一个位置p (l - 1 <= p <= r - 1),使得s[p] xor val 最大
3.限制1: p <= r - 1,可直接用可持久化Trie维护,答案从root[r - 1]中找即可
4.限制2: p >= l - 1,维护每个点的max_id。含义是:当前版本中 用来更新 当前点的 最大下标i
(p >= l - 1 等价于 最大的i 大于 l - 1)
递归实现 方便统计max_Id,读者可自行体会,事实上,每次执行insert都会重新开一个新的根节点,也就是新的版本。并递归的插入s[i]的每一个二进制位.对于所有新插入的节点而言,其max_id都会被更新为i;若不是新插入的点,则直接复制之前版本的信息,之前版本的信息中也包含了历史版本的max_id.
总之,查询某一个版本的trie时,所有新插入的点都会被更新为i,而旧的点则继承历史版本信息
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 600010, M = N * 25;
int n,m;
int tr[M][2],max_id[M],idx;
int root[N];
int s[N];
void insert(int i, int k, int p, int q)
{
if(k < 0)
{
max_id[q] = i;
return ;
}
int v = s[i] >> k & 1;
if(p) tr[q][v ^ 1] = tr[p][v ^ 1];
//p存在的话,将与当前扩展节点相反的历史版本直接复制过来
tr[q][v] = ++ idx;
insert(i, k - 1, tr[p][v], tr[q][v]);
max_id[q] = max(max_id[tr[q][0]], max_id[tr[q][1]]);
}
int query(int root, int C, int L)
{
int q = root;
for(int i = 23; ~i; i --)
{
int v = C >> i & 1;
//如果当前节点的相反节点 node
//如果node是由 >= L的版本更新
if(max_id[tr[q][v^1]] >= L)
{
q = tr[q][v^1];
}
else q = tr[q][v];
}
return C ^ s[max_id[q]];
}
int main()
{
cin >> n >> m;
//0也是合法方案
root[0] = ++idx;
max_id[0] = -1;
//23是因为1e7的数据范围
insert(0, 23, 0, root[0]);
for(int i = 1; i <= n; i ++ )
{
int a; cin >> a;
s[i] = s[i - 1] ^ a;
root[i] = ++idx;
insert(i, 23, root[i - 1], root[i]);
}
for(int i = 1; i <= m; i ++ )
{
char op[2];
scanf("%s", op);
if(op[0] == 'A')
{
int x; cin >> x;
n ++;
s[n] = s[n - 1] ^ x;
root[n] = ++idx;
insert(n, 23, root[n - 1], root[n]);
}
else
{
int l,r,x;
cin >> l >> r >> x;
int val = x ^ s[n];
cout << query(root[r - 1], val, l - 1) << endl;
}
}
return 0;
}