在https://blog.csdn.net/fengbingchun/article/details/130039337 中介绍了相机外参及相机的位姿R,t,其中R为3*3旋转矩阵(R的逆矩阵与R的转置矩阵相同),t为3*1平移向量,R,t组合成3*4的矩阵。
在instant-ngp中执行scripts/colmap2nerf.py过程中,colmap会生成colmap_text/images.txt文件,此文件包含相机的外参信息,每两行定义一幅图像的信息:
IMAGE_ID, QW, QX, QY, QZ, TX, TY, TZ, CAMERA_ID, NAME
POINTS2D[] as (X, Y, POINT3D_ID) 其中,QW, QX, QY, QZ, TX, TY, TZ为相机的外参,四元数(QW, QX, QY, QZ)和平移向量(TX, TY, TZ),四元数(quaternion)是使用Hamilton约定来定义的。
注:以下内容来自网络整理
在空间中准确定位、移动和旋转物体可以通过多种方式完成。更熟悉和更容易可视化的欧拉角(roll, pitch, yaw)是有限的,在某些情况下应该用更强大的四元数代替。
四元数是用于旋转和拉伸(stretch)向量的数学运算符。
威廉·汉密尔顿(William Rowan Hamilton)在1843年发明了四元数,作为一种方法,允许他对向量进行乘法和除法,旋转和拉伸它们。
四元数的两种表示:一个四元数q拥有一个实部和三个虚部;q0,q1,q2,q3为实数;i,j,k为虚部的三个基;其实部可能位于第一位,也可能位于最后一位
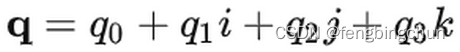
(1).Hamilton: ijk=-1
(2).JPL: ijk=1
四元数Hamilton形式转旋转矩阵:
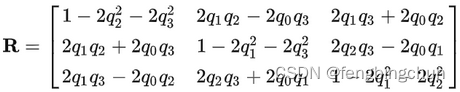
旋转矩阵转四元数Hamilton形式,参考: matrixToQuaternion
以下分别调用opencv, eigen, pyquaternion接口的实现:
1.opencv的实现:
void quaternion_to_rotate_matrix(double qvec[4])
{
double m11 = 1 - 2 * std::pow(qvec[2], 2) - 2 * std::pow(qvec[3], 2);
double m12 = 2 * qvec[1] * qvec[2] - 2 * qvec[0] * qvec[3];
double m13 = 2 * qvec[3] * qvec[1] + 2 * qvec[0] * qvec[2];
double m21 = 2 * qvec[1] * qvec[2] + 2 * qvec[0] * qvec[3];
double m22 = 1 - 2 * std::pow(qvec[1], 2) - 2 * std::pow(qvec[3], 2);
double m23 = 2 * qvec[2] * qvec[3] - 2 * qvec[0] * qvec[1];
double m31 = 2 * qvec[3] * qvec[1] - 2 * qvec[0] * qvec[2];
double m32 = 2 * qvec[2] * qvec[3] + 2 * qvec[0] * qvec[1];
double m33 = 1 - 2 * std::pow(qvec[1], 2) - 2 * std::pow(qvec[2], 2);
std::cout << "result:" << "\n";
std::cout << "[" << m11 << ", " << m12 << ", " << m13 << ";" << "\n";
std::cout << m21 << ", " << m22 << ", " << m23 << ";" << "\n";
std::cout << m31 << ", " << m32 << ", " << m33 << "]" << "\n";
}
int test_quaternion()
{
std::vector<double> data = {
2.044289726145588e-004, -0.2587487517264626, -0.9659446369688031,
-0.9993063898830017, -3.602307923217642e-002, 9.438056030485108e-003,
-3.723838540803551e-002, 0.9652727185840433, -0.2585766451355823
};
// 1. rotate matrix to quaternion(Hamilton)
cv::Mat mat(3, 3, CV_64FC1, data.data());
cv::Quatd q1 = cv::Quatd::createFromRotMat(mat);
std::cout.precision(16);
std::cout << "w:" << q1.w << ", x:" << q1.x << ", y:" << q1.y << ", z:" << q1.z << "\n";
// 2. quaternion(Hamilton) to rotate matrix
cv::Quatd q2 = cv::Quatd(q1.w, q1.x, q1.y, q1.z);
cv::Matx<double, 3, 3> R = q2.toRotMat3x3();
std::cout << R << "\n";
double arr[4] = { q1.w, q1.x, q1.y, q1.z };
quaternion_to_rotate_matrix(arr);
return 0;
}执行结果如下所示:
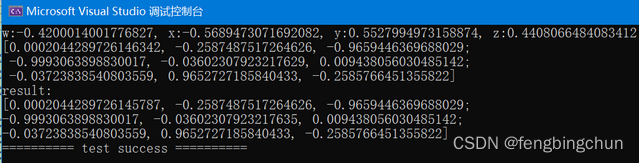
2.Eigen的实现:
int test_quaternion()
{
Eigen::Matrix3d matrix3d;
matrix3d << 2.044289726145588e-004, -0.2587487517264626, -0.9659446369688031,
-0.9993063898830017, -3.602307923217642e-002, 9.438056030485108e-003,
-3.723838540803551e-002, 0.9652727185840433, -0.2585766451355823;
// 1. rotate matrix to quaternion(Hamilton)
Eigen::Quaterniond q;
q = matrix3d;
std::cout.precision(16);
std::cout << "w:" << q.w() << ", x:" << q.x() << ", y:" << q.y() << ", z:" << q.z() << "\n";
// 2. quaternion(Hamilton) to rotate matrix
Eigen::Quaterniond q2(q.w(), q.x(), q.y(), q.z());
Eigen::Matrix3d R = q2.toRotationMatrix();
std::cout << "R:\n" << R << "\n";
return 0;
}执行结果如下图所示:
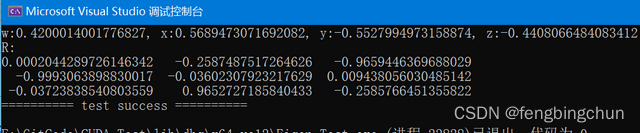
3.Python的pyquaternion实现:
import numpy as np
from pyquaternion import Quaternion
def calculate_quaternion(R):
q = Quaternion(matrix=np.array(R))
return q
def calculate_rotate_matrix(q):
R = q.rotation_matrix
return R
def qvec2rotmat(qvec):
# from instant-ngp/scripts/colmap2nerf.py
return np.array([
[
1 - 2 * qvec[2]**2 - 2 * qvec[3]**2,
2 * qvec[1] * qvec[2] - 2 * qvec[0] * qvec[3],
2 * qvec[3] * qvec[1] + 2 * qvec[0] * qvec[2]
], [
2 * qvec[1] * qvec[2] + 2 * qvec[0] * qvec[3],
1 - 2 * qvec[1]**2 - 2 * qvec[3]**2,
2 * qvec[2] * qvec[3] - 2 * qvec[0] * qvec[1]
], [
2 * qvec[3] * qvec[1] - 2 * qvec[0] * qvec[2],
2 * qvec[2] * qvec[3] + 2 * qvec[0] * qvec[1],
1 - 2 * qvec[1]**2 - 2 * qvec[2]**2
]
])
if __name__ == "__main__":
R = [[2.044289726145588e-004, -0.2587487517264626, -0.9659446369688031],
[-0.9993063898830017, -3.602307923217642e-002, 9.438056030485108e-003],
[-3.723838540803551e-002, 0.9652727185840433, -0.2585766451355823]]
q = calculate_quaternion(R)
print(f"quaternion:\n{q}")
R2 = calculate_rotate_matrix(q)
print(f"R2:\n{R2}")
R3 = qvec2rotmat([q[0], q[1], q[2], q[3]])
print(f"R3:\n{R3}")
print("test finish")执行结果如下图所示:
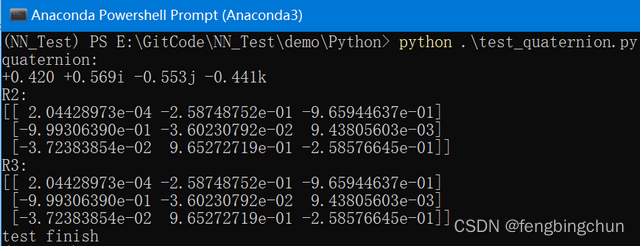
由以上输出结果可知:
(1).旋转矩阵转四元数:pyquaternion和eigen结果一致;opencv与其它两者w,x和y,z只是符号相反,数值相同;还不清楚原因
(2).四元数转旋转矩阵:pyquaternion和eigen结果一致;opencv由四元数结果同样能转回到之前的原旋转矩阵
GitHub:
https://github.com/fengbingchun/NN_Test
https://github.com/fengbingchun/CUDA_Test


![[答疑]UML精粹里和你视频里说的不太一样](https://img-blog.csdnimg.cn/img_convert/3d2a599f693e61eb96599b288a040fc1.png)