完全二叉树

空树也算是完全二叉树
每一层都是满的也算是完全二叉树
如果层不满，那这层必须要是最底层并且是一个从左往右准备填满的状态。

图中，上面那个是完全二叉树，下面的不是。
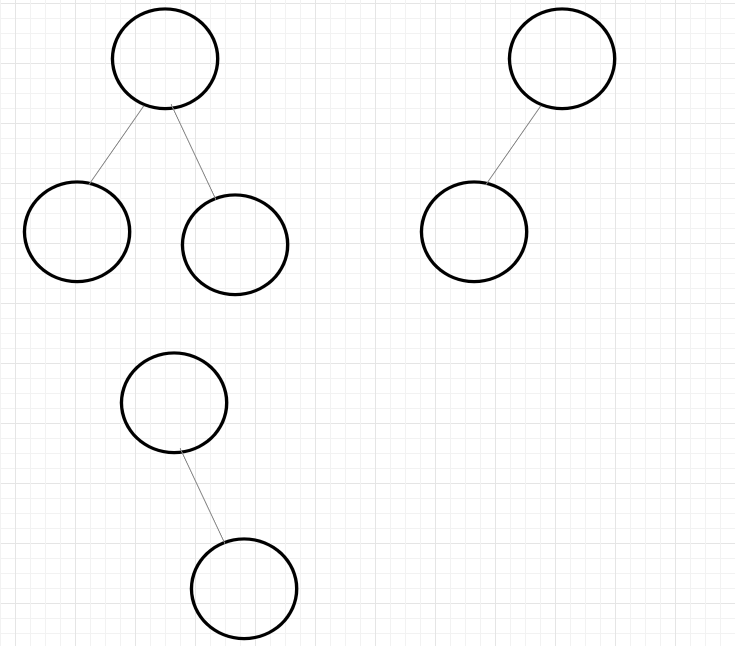
在这里插入图片描述

用数组结构表示完全二叉树

从0位置开始的一段连续数组，可以被认为是一个完全二叉树。可以想象数组0位置相当于是二叉树的头结点，单独只有0位置时，也算是完全二叉树，后续1、 2相当于躺在了0的左右侧，以此类推。
那从数组出发连续的这一段，就可以在脑海中生成一个完全二叉树。
那么这样的一个完全二叉树有这么一个规律。
任何一个索引下标位置为 i 的节点来讲，左子节点在数组中位置：i * 2 + 1 右子节点在数组中位置： i * 2 + 2 父节点在数组位置： i - 1 / 2向下取整。
那如果说数组的长度是1000，但是脑海中形成二叉树的范围只有 0 ~ 7，那就可以用一个heapSize的变量来看当前二叉树的中节点的一个数量，数组中超过7的部分在二叉树中不存在，不用关注。

堆

堆就是一个完全二叉树，而堆又分为大根堆和小根堆。

大根堆
在完全二叉树中，每一棵子树的最大值，都是头节点的值。

小根堆
在完全二叉树中，每一棵子树的最小值，都是头节点的值。

图中就是一个大根堆，最大值为头结点，8、5、6分别为对应树的头结点的最大值。
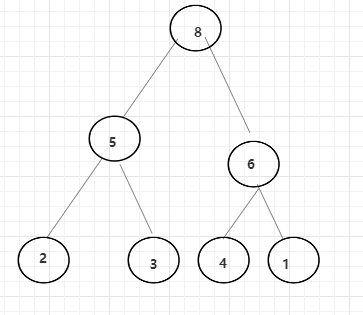
在这里插入图片描述

用数组实现堆结构

假设现在有一个长度为1000的数组，但目前heapSize = 0，因为当前的heap中没有数据，有一个add(int num)方法，这个方法会接收一个整数，通过接收的整数和数组，来实现一个大根堆的结构。

首先通过add方法接收到数字10，此时heapSize = 0，二叉树中没有数据，10进来以后，依然满足大根堆的结构，heapSize = 1，10在数组中的位置是0，
依次再接收8，6，都比10小，所以作为10的左右两个子树。
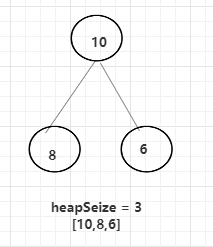
在这里插入图片描述
此时，再次调用add()方法，接收的数值是12，正常应该是8的左子树，但是由于大根堆的特性，12需要和父节点进行比较（i -1 / 2 ），算出此时的父节点的8（数组中索引位置是1），大则需要进行交换，在数组中的体现就是两个元素调换位置，换完之后再次找父节点（10）进行比较，发现12比10也大，再次交换，此时的父节点是0，代表自己就是父节点，结束。
整体过程如下：
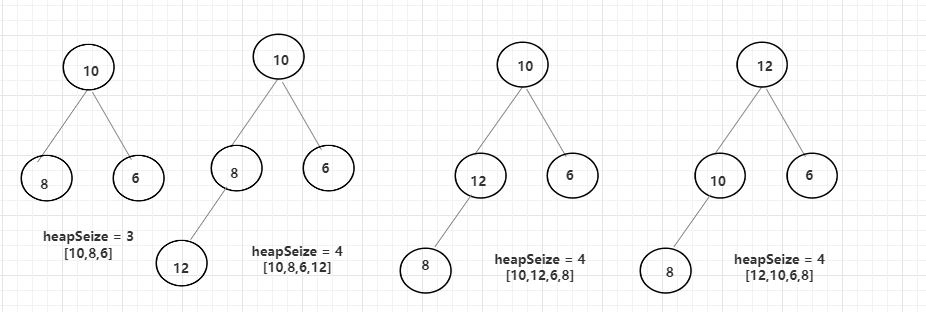
在这里插入图片描述
总结起来上面的步骤就是在加入新数时，为了保持大根堆的数据结构，需要不停的和父节点进行比较，如果比父节点大，则交换，知道自己成为父节点或不再比父节点大为止。
代码实现：

 	//新加的数在数组中index的位置
    //循环，直到自己成为父节点，或者没有父节点的数大 为止。
    private void heapInsert(int[] arr, int index) {
        while (arr[index] > arr[(index - 1) / 2]) {
            swap(arr, index, (index - 1) / 2);
            //数值交换后，索引也要更改，继续和父节点进行比较
            index = (index - 1) / 2;
        }
    }

    private void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
         arr[i] =  arr[j];
         arr[j] = tmp;
    }

上面已经完成了基本的添加功能，那么如果这时需要获取到大根堆中最大的数并在大根堆中移除它呢？由于大根堆的特性，头结点（也就是arr[0]位置）的数，就是大根堆中最大的数，那么只需要利用一个变量保存它返回就可以，但是在返回之前，因为最大的数已经返回了，所以还需要调整大根堆的结构。
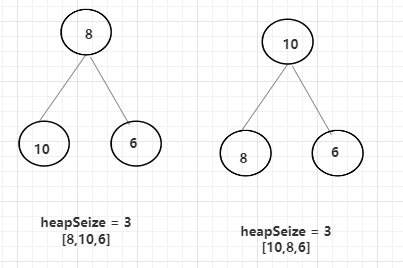
在这里插入图片描述
12弹出后，会将最末端的8先作为头节点，heapSize相对-1，但是因为大根堆的特性，8是需要跟左右子节点进行比较，并选出较大的一个作为新的头结点，交换后，8还要一次和左右子节点进行比较，知道大于等于左右子节点为止。
代码实现：

 private void heapify(int[] arr, int index, int heapSize) {
        //找出左子节点的下标
        int left = index * 2 + 1;
        //看是否有左子节点
        //因为heapSize是存储heap中节点的数量，所以 leaf只能< heapSize 不能等于，否则下标可能会越界
        while (left < heapSize) {
            //left + 1求的是右子节点的值，看右子节点是否存在，
            //并且取左右子节点中较大的一个数
            int largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1 : left;
            //这一步是判断 我左右子节点中较大的那个数，是否大于我当前位置的数
            //如果大于，则获取它的下标，准备交换
            largest = arr[largest] > arr[index] ? largest : index;
            //如果等于，说明没有交换的必要
            if (largest == index) {
                break;
            }
            swap(arr, largest, index);
            //数据交换后，当前数的位置也要跟着变化
            index = largest;
            //再次获取左子节点的位置。
            left = index * 2 + 1;
        }
    }

时间复杂度

因为有关堆的操作只有heapInsert和heapify，那每次heapInsert时，只需要跟父节点进行比较，heapify虽然会和左右子节点进行比较，但是只会选择一个下沉。所以堆的时间复杂度是 $O (l o g N)$ 级别的。
因为堆几乎是一个完全二叉树，所以当堆中有一个数据时，高度是0，有3个数据高度是2，有7个数据高度是3，以此类推。

无序数组用大根堆排序

先将无序数组构建成大根堆的结构，因为大根堆父节点大于子节点的特性，所以每次将最末端的数和0位置的数做交换，并且–heapSize，–heapSize后，弹出的数就相当于断联，就在应该有的位置上了。新到0位置的数调用heapify进行调整。直到heapSize为1。

public static void heapSort(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }

        for (int i = 0; i < arr.length; i++) {
            heapInsert(arr, i);
        }

        int heapSize = arr.length;
        swap(arr, 0, --heapSize);
        while (heapSize > 0) {
            heapify(arr, 0, heapSize);
            swap(arr, 0, --heapSize);
        }
    }