目录

---

关于“取整”

"取整"规则

1、向零取整 

2、向-∞取整

3、向+∞取整

4、四舍五入

关于"取模和取余"

运算符优先级 

---

关于“取整”

#include <stdio.h>
int main()
{
	//本质是向0取整
	int i = -2.9;
	int j = 2.9;
	printf("%d\n", i); //结果是：-2
	printf("%d\n", j); //结果是：2
	return 0;
}

        我们可以发现上面的代码在求 a / 2 的值得过程中进行了取整操作，因为在数学中 5 / 2 的结果为2.5，而我们上面的打印结果确实 2，但是为什么是2呢？在数学中2.5应该四舍五入是3，为什么结果不是3呢？这就要讲到我们取整的规则了。

"取整"规则

1、向零取整 

#include <stdio.h>
#include <tgmath.h>
int main()
{
	//本质是向0取整
	int i = -2.9;
	int j = 2.9;
	printf("%d\n", i); //结果是：-2
	printf("%d\n", j); //结果是：2

	printf("%d\n", (int)trunc(2.9));//结果是：2
	printf("%d\n", (int)trunc(-2.9));//结果是：-2
	return 0;
}

        这段代码演示了C语言中向零取整的方法。它使用了tgmath.h库中的trunc()函数来进行向零取整的操作。我们来解释一下这段代码的具体实现过程：

1. 首先，代码包含了stdio.h和tgmath.h两个库文件，前者提供了C语言标准I/O库的支持，后者提供了数学函数库的支持。

2. 接着，在main函数中定义了两个整型变量i和j，并将其分别初始化为-2.9和2.9。由于i和j的类型为整型，因此在初始化时，浮点数部分会被截断，只保留整数部分，i的值为-2，j的值为2。

3. 然后，代码使用printf()函数分别打印了变量i和j的值。打印结果分别为-2和2，符合预期。

4. 接下来，代码使用trunc()函数对2.9和-2.9进行了向零取整的操作，并将结果强制转换成整型，然后使用printf()函数打印了结果。向零取整的过程中，该函数会将小数部分直接截断，只保留整数部分。由于2.9和-2.9的小数部分分别为0.9和-0.9，因此向零取整后的结果分别为2和-2。

        总之，这段代码演示了C语言中向零取整的方法，使用trunc()函数可以轻松实现该操作。

2、向-∞取整

#include <stdio.h>
#include <tgmath.h> //因为使用了floor函数，需要添加该头文件
int main()
{
	//本质是向-∞取整，注意输出格式要不然看不到结果
	printf("%.1f\n", floor(-2.9)); //-3
	printf("%.1f\n", floor(-2.1)); //-3
	printf("%.1f\n", floor(2.9)); //2
	printf("%.1f\n", floor(2.1)); //2
	return 0;
}

        这段代码演示了C语言中向-∞取整（floor）的方法。它使用了tgmath.h库中的floor()函数来进行向下取整的操作。我们来解释一下这段代码的具体实现过程：

1. 首先，代码包含了stdio.h和tgmath.h两个库文件，前者提供了C语言标准I/O库的支持，后者提供了数学函数库的支持。

2. 接着，在main函数中使用floor()函数对四个浮点数进行向下取整的操作，并使用printf()函数打印了四个结果。在使用printf()函数时，使用了格式化输出，%.1f指输出一个浮点数，保留一位小数（四舍五入）。这里特别注意，我们在使用格式化输出时，必须使用%f来输出浮点数，而不能使用%d来输出整数，因为%d会将浮点数转换成整数，并截取掉小数部分，造成输出错误。

3. 向-∞取整的过程中，floor()函数会将浮点数向-∞取整到最接近且小于等于该数的整数。例如，-2.9的向下取整结果为-3，而2.1的向下取整结果为2，符合预期。

        总之，这段代码演示了C语言中向-∞取整的方法，使用floor()函数可以轻松实现该操作。在使用printf()函数输出结果时，需要注意格式化输出的使用，以避免数据类型截断和输出错误。

3、向+∞取整

#include <stdio.h>
#include <tgmath.h>
int main()
{
	//本质是向+∞取整，注意输出格式要不然看不到结果
	printf("%.1f\n", ceil(-2.9)); //-2
	printf("%.1f\n", ceil(-2.1)); //-2
	printf("%.1f\n", ceil(2.9)); //3
	printf("%.1f\n", ceil(2.1)); //3
	return 0;
}

        这段代码演示了C语言中向+∞取整（ceil）的方法。它使用了tgmath.h库中的ceil()函数来进行向+∞取整的操作。我们来解释一下这段代码的具体实现过程：

1. 首先，代码包含了stdio.h和tgmath.h两个库文件，前者提供了C语言标准I/O库的支持，后者提供了数学函数库的支持。

2. 接着，在main函数中使用ceil()函数对四个浮点数进行向+∞取整的操作，并使用printf()函数打印了四个结果。在使用printf()函数时，使用了格式化输出，%.1f指输出一个浮点数，保留一位小数（四舍五入）。同样，我们也需要注意输出格式。

3. 向+∞取整的过程中，ceil()函数会将浮点数向+∞取整到最接近且大于等于该数的整数。

4、四舍五入

#include <stdio.h>
#include <tgmath.h>
int main()
{
	//本质是四舍五入
	printf("%.1f\n", round(2.1));
	printf("%.1f\n", round(2.9));
	printf("%.1f\n", round(-2.1));
	printf("%.1f\n", round(-2.9));
	return 0;
}

        

这是一个C语言程序，功能是使用`<tgmath.h>`头文件中的`round()`函数进行四舍五入操作，并输出结果。

具体解释如下：

1. `#include <stdio.h>`和`#include <tgmath.h>`是C语言的头文件，用于引入标准输入输出和复数数学库。

2. `int main()`是程序的主函数，表示程序从这里开始执行。

3. `printf()`是C语言的输出函数，用于将格式化的数据输出。

4. `round()`是`<tgmath.h>`库中的函数，用于对一个浮点数进行四舍五入操作。其返回值也是一个浮点数，结果取决于函数参数的小数部分。如果小数部分大于等于0.5，则向正无穷方向舍入；否则向负无穷方向舍入。

5. `%.1f`是输出格式控制符，表示输出一个浮点型数值并精确到小数点后一位。

6. `return 0`是程序正常结束时返回的值。此处表示程序成功执行完毕，并将0作为返回值。

总结

关于"取模和取余"

取模概念：

        如果a和d是两个自然数，d非零，可以证明存在两个唯一的整数 q 和 r，满足 a = q*d + r 且0 ≤ r < d。其中，q 被称为商，r 被称为余数。

#include <stdio.h>
int main()
{
	int a = 10;
	int d = 3;
	printf("%d\n", a % d); //结果是1
	//因为：a=10,d=3,q=3,r=1 0<=r<d(3)
	//所以：a = q*d+r -> 10=3*3+1
	return 0;
}

如果是下面的代码呢?

#include<stdio.h>
int main()
{
	int a = -10;
	int d = 3;
	printf("%d\n", a/d); //C语言中是-3
	printf("%d\n", a % d);//结果是-1
	return 0;
}

上面的是在c语言编译器的结果，下面是python编译器出现的结果。

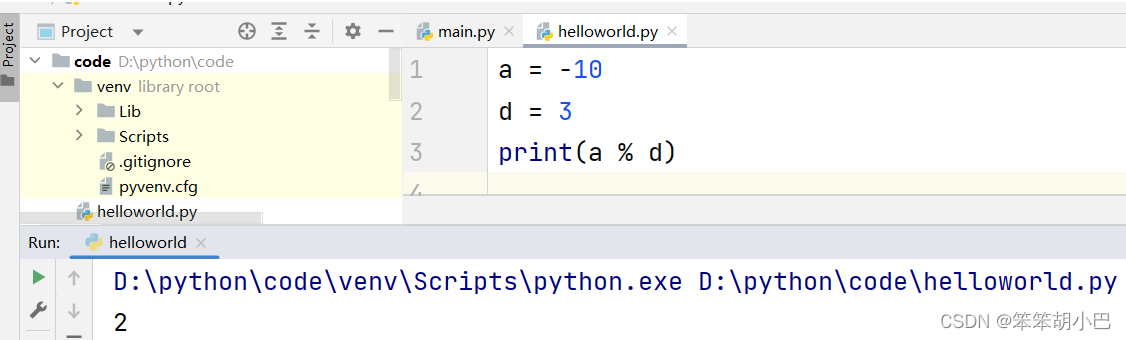
结论：很显然，上面关于取模的定义，并不能满足语言上的取模运算。

是什么决定了这种现象

        由上面的例子可以看出，具体余数r的大小，本质是取决于商q的。 而商，又取决谁呢？取决于除法计算的时候，取整规则。

        在c语言中，我们求得得商是-3，因为c语言的取整规则是向零取整。而在python中，我们求的商是-4，这是因为python中的取整规则是向-∞取整。

取余和取模一样吗？

        细心的同学，应该看到了，我上面的取模都是带着" "的。说明这两个并不能严格等价(虽然大部分情况差不多)
取余或者取模，都应该要算出商，然后才能得出余数。

本质 1 取整：
取余：尽可能让商，进行向0取整。
取模：尽可能让商，向 -∞方向取整。

故：
C中%, 本质其实是取余。
Python中% ，本质其实是取模。

理解：

        
        对任何一个大于0的数，对其进行0向取整和 - ∞取整，取整方向是一致的。故取模等价于取余。
        对任何一个小于0的数，对其进行0向取整和 - ∞取整，取整方向是相反的。故取模不等价于取余。

同符号数据相除，得到的商，一定是正数（正数vs正整数），即大于0！
故，在对其商进行取整的时候，取模等价于取余。

本质 2 符号：
参与取余的两个数据，如果同符号，取模等价于取余。 

        c语言环境下：

     python语言环境下：

如果参与运算的数据，不同符号呢？

明显结论：如果不同符号，余数的求法，参考之前定义。而余数符号，与被除数相同。

 很明显，不符合上面的规律，余数符号，与被除数完全相反。这是为什么呢？

总结：

1、浮点数(或者整数相除)，是有很多的取整方式的。

2、如果a和d是两个自然数，d非零，可以证明存在两个唯一的整数 q 和 r，满足 a = q*d + r , q 为整数，且0 ≤ |r| < |d|。其中，q 被称为商，r 被称为余数。

3、在不同语言，同一个计算表达式，“取模”结果是不同的。我们可以称之为分别叫做正余数 和 负余数

4、具体余数r的大小，本质是取决于商q的。而商，又取决于除法计算的时候，取整规则。 5、取余vs取模： 取余尽可能让商，进行向0取整。取模尽可能让商，向-∞方向取整。

6、参与取余的两个数据，如果同符号，取模等价于取余

7、如果参与取余的两个数据符号不同，在C语言中(或者其他采用向0取整的语言如：C++，Java)，余数符号，与被 除数相同。（因为采用的向0取整）

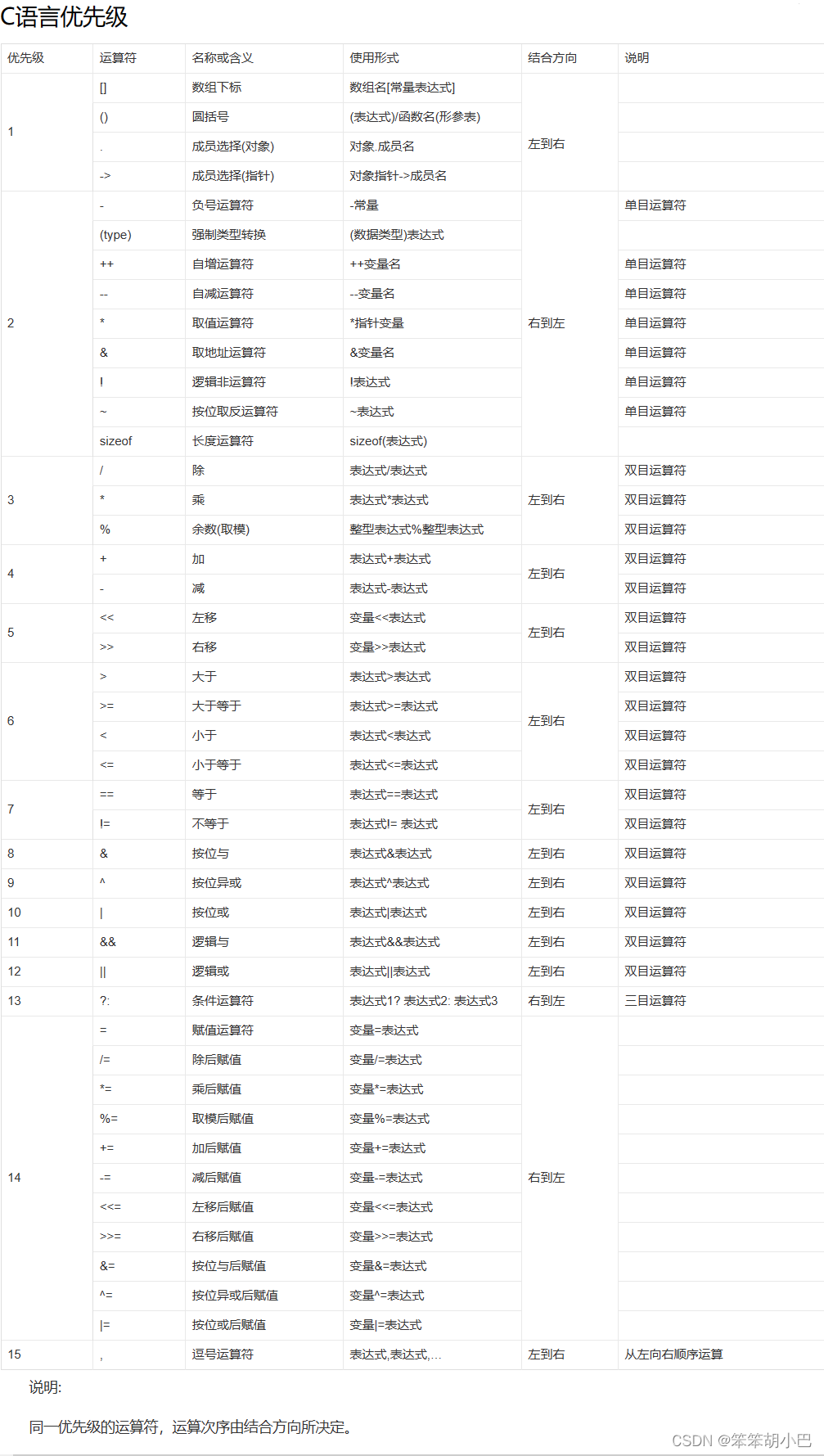
运算符优先级