文章目录
- 一、简介与使用场景
- 二、算法思想
- 三、朴素版Dijkstra
- 四、堆优化版Dijkstra
- 五、总结
一、简介与使用场景
迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法。这是从一个顶点到其余各顶点的最短路径算法,解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始,采用贪心算法的策略,每次遍历到始点距离最近且未访问过的顶点的邻接节点,直到扩展到终点为止。
Dijkstra算法的使用场景:
一定要是单源最短路径且每条边的权重必须是正值
单源最短路径:希望找到从(一个)源节点到每个结点的最短路径;
二、算法思想
Dijkstra算法主要是基于贪心的策略,始终保持当前迭代解为当前最优解。意思就是在已知的条件下或是当前拥有的全部条件下保证最优解,若在此后的迭代中由于加入了新的条件使得产生了更优解则替代此前的最优解。通过不断的迭代不断保证每次迭代的结果都是当前最优解,当迭代到最后一轮时得到的就会是全局最优解。
步骤:
比如说现在要求1到n节点的最短距离。
我们可以用一个bool数组st记录每个边是否已经被确定为最短路。
再用一个dist数组记录每个节点到源点的距离。
1️⃣ 先把第一个节点的距离记为0(dist[1] = 0),其他的节点距离记为正无穷。
2️⃣ 循环n - 1次,每一次循环内部再遍历所有节点,找到(不在st数组内的)最小权值的节点。再把这个节点加入到st中。
3️⃣ 用找到的这个节点更新其他(与他相连)节点的dist。
第一次找到x节点的时候一定从源点到x节点的最短路径。
举个例子:

先把①的dist变成0,其他的dist为正无穷。
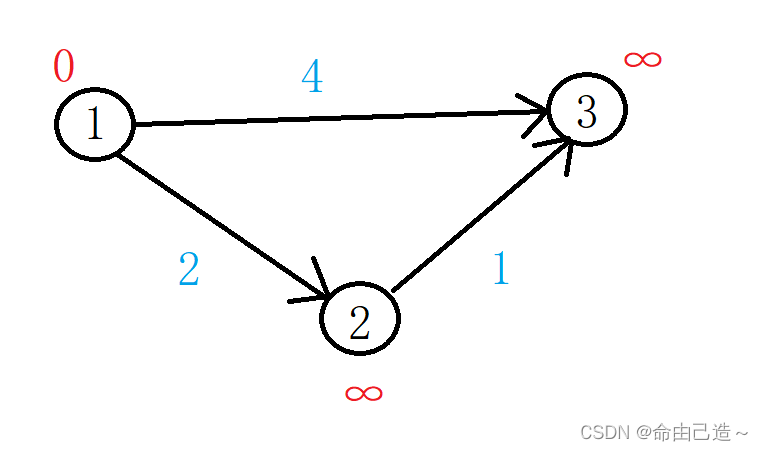
循环两次,第一次找到了①节点。然后利用①更新没有确定已经是最短路径的节点,也就是2和3。而此时①就已经确定了他自己的最短路径,标记st为true。
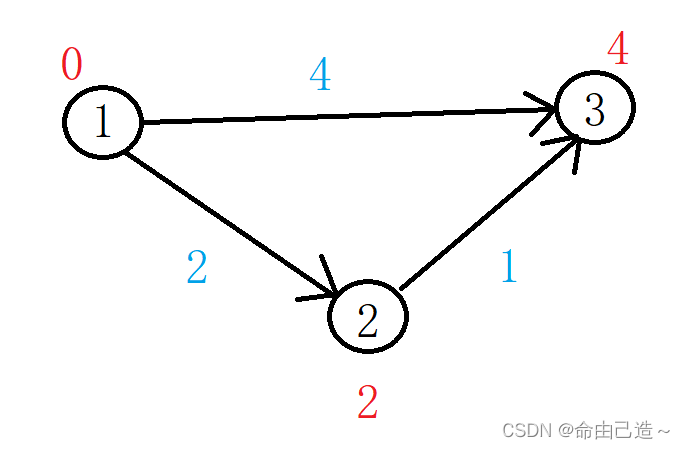
第二次循环找到了②节点,那么利用②来处理还没有确定的节点,只剩下③。
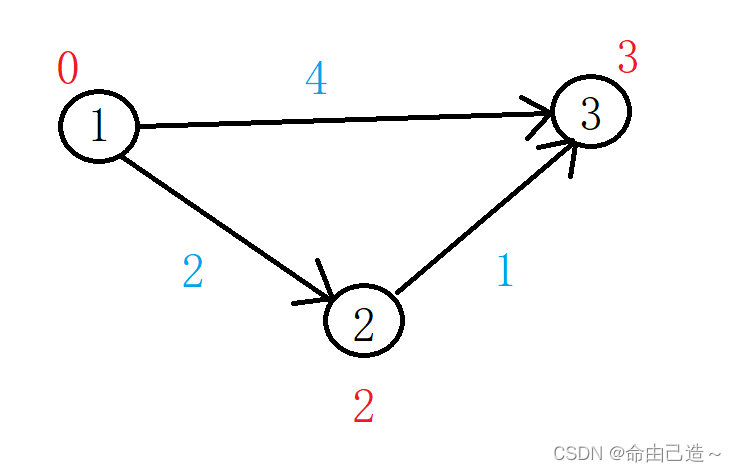
由此单源最短路径就已经找到。
三、朴素版Dijkstra
用一道例题来讲解:
题目链接
题目描述:
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为正值。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 −1。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 −1。
数据范围
1≤n≤500,1≤m≤105,
图中涉及边长均不超过10000。
输入样例:
3 3
1 2 2
2 3 1
1 3 4
输出样例:
3
思路分析:
因为这道题的给的是稠密图,所以用邻接矩阵来存储。
而存在重边所以初始化邻接矩阵的时候每次要判断是不是最小,取最小值即可。
而如果存在自环,只需要最后判断n节点有没有被处理即可。
#include <iostream>
#include <cstring>
using namespace std;
const int N = 510;
int n, m;
int g[N][N];// 邻接矩阵
int dist[N];// 距离
bool st[N];// 是否已经确定了最短路径
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;// 初始化第一个节点
for(int i = 0; i < n - 1; i++)// 循环n - 1次
{
int t = -1;// 找最小节点
for(int j = 1; j <= n; j++)
{
if(!st[j] && (t == -1 || dist[j] < dist[t]))
{
t = j;
}
}
if(t == n) break;// 找了n节点是最小说明n已经确定为最短路径了
st[t] = true;
// 更新其他节点
for(int j = 1; j <= n; j++)
{
dist[j] = min(dist[j], dist[t] + g[t][j]);
}
}
if(dist[n] == 0x3f3f3f3f) return -1;
else return dist[n];
}
int main()
{
memset(g, 0x3f, sizeof g);
cin >> n >> m;
int a, b, c;
while(m--)
{
cin >> a >> b >> c;
g[a][b] = min(g[a][b], c);
}
cout << dijkstra() << endl;
return 0;
}
四、堆优化版Dijkstra
而如果题目给的是一个稀疏图,我们还用上面的算法(时间复杂度为O(N^2)),可能会超时。
所以有了一个优化版本的Dijkstra算法。
通过分析朴素版本的代码,可以看到每次都要暴力遍历所有的边找到最小的距离,所以我们可以使用堆,每次堆顶都是最小的边。
来看一道例题:
题目链接
题目描述:
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为非负值。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 −1。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 −1。
数据范围
1≤n,m≤1.5×105,图中涉及边长均不小于 0,且不超过 10000。
数据保证:如果最短路存在,则最短路的长度不超过 109。
输入样例:
3 3
1 2 2
2 3 1
1 3 4
输出样例:
3
思路描述:
大致思路跟朴素版一样,而我们怎么用优先级队列来得到最小距离的节点呢?
我们可以用pair<int, int>来存储,first代表距离,second代表节点。
这里用数组模拟邻接表在上一章有讲解:
【数据结构与算法】图——邻接表与邻接矩阵
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 150010;
int n, m;
int h[N], e[N], ne[N], w[N], idx;
bool st[N];
int dist[N];
void add(int a, int b, int c)
{
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx++;
}
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
priority_queue<PII, vector<PII>, greater<PII>> pq;
pq.push({0, 1});
dist[1] = 0;
while(pq.size())
{
auto t = pq.top();
pq.pop();
int node = t.second, val = t.first;
if(st[node]) continue;
st[node] = true;
// 更新其他节点
for(int i = h[node]; i != -1; i = ne[i])
{
int j = e[i];
dist[j] = min(dist[j], w[i] + dist[node]);
pq.push({dist[j], j});
}
}
if(dist[n] == 0x3f3f3f3f) return -1;
else return dist[n];
}
int main()
{
memset(h, -1, sizeof h);
cin >> n >> m;
int a, b, c;
while(m--)
{
cin >> a >> b >> c;
add(a, b, c);
}
cout << dijkstra() << endl;
return 0;
}
五、总结
Dijkstra算法用来解决的是单源最短路径且没有负权值的问题。
并不是所有的题目都用优化版本的,而是稠密图用朴素版Dijkstra,稀疏图用堆优化版Dijkstra。