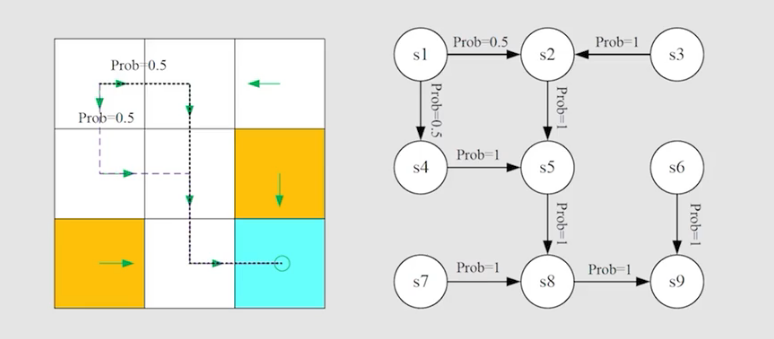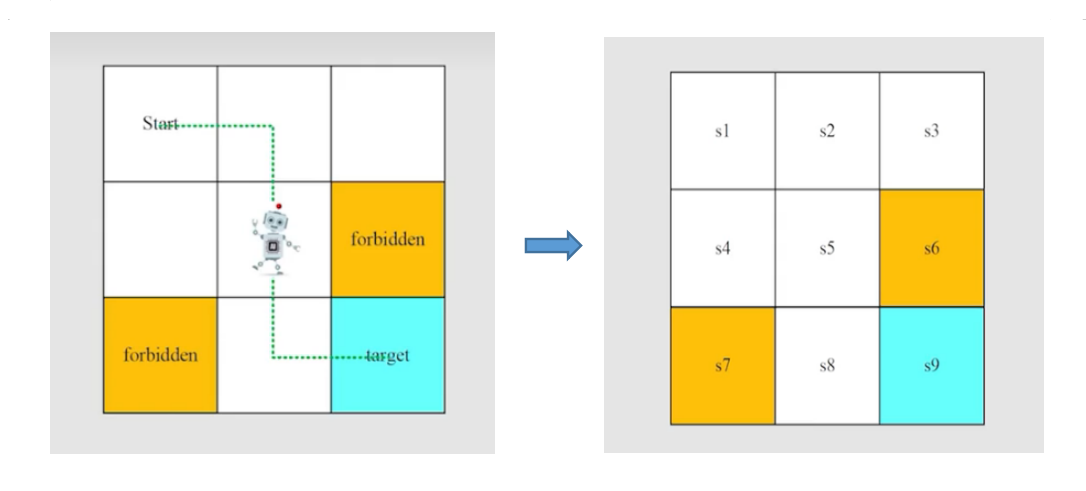
以 grid-world 为例，进行强化学习基础概念的介绍。如图，机械人处于一个网格世界中，不同的网格代表不同的功能，白色代表机械人可以自由的进入，黄色代表陷阱（机械人一旦进入就会被强制返回起点），蓝色代表终点，现在要求机械人自己学习，从起点到终点走最短路径。

状态 state

状态：系统在各阶段可能发生的状态$S_i$，如图状态有$s1$,$s2$, ···,$s9$

状态集合：系统在各阶段所有可能发生的状态的集合 $S$=$\{\begin{array}{l}{S}_i\end{array}\}$

行为 action

行为：在每个状态可能采取的行为 $a_i$。在grid-world中机械人共有5种行为：
  $a1$:向上移动;
  $a2$: 向右移动;
  $a3$: 向下移动;
  $a4$: 向左移动;
  $a5$: 保存原位置不动;

行为集合：所有的可采取行为的集合$A(S_i)$=$\{\begin{array}{l}{a}_i\end{array}\}$

状态转移

状态转移：一个状态通过采取一个行为后会转移到另一个状态 $S_1—a2—>S_2$

状态转移概率：用概率来描述状态转换！
       $p(s_j|s_i,a_n)$：表示在状态 $s_i$ 采取行为 $a_n$ 到达状态$s_j$的概率
       如：$p(s_2|s_1,a_2)=1$

策略 policy

策略：基于最终的目的指导当前状态下应该采取什么的行为，每个状态都对应有一个策略
   例如现在给出一个策略 (绿色箭头表示策略) ，如下图，那么基于给出的策略会得到不同起点到达终点的路径。

   在具体问题中，常常运用数学中的条件概率表示策略，强化学习中习惯性用 $\pi$ 表示策略，$\pi (a_n|s_i)$ 表示在状态 $s_i$ 的条件下采取行为 $a_n$ 的概率。
   以状态$s1$为例，上面给出箭头的策略用数学表达形式如下（确定性概率）：
$$\pi (a_1|s_1)=0$$$$\pi (a_2|s_1)=1$$$$\pi (a_3|s_1)=0$$$$\pi (a_4|s_1)=0$$$$\pi (a_5|s_1)=0$$
   以状态$s1$为例，不确定性概率的策略：

$$\pi (a_1|s_1)=0$$$$\pi (a_2|s_1)=0.5$$$$\pi (a_3|s_1)=0.5$$$$\pi (a_4|s_1)=0$$$$\pi (a_5|s_1)=0$$

在编程中，策略通常使用数组（矩阵）的形式表示：

奖励 reward

   在强化学习中，奖励是一个实数(标量)，是采取行为后获得的。奖励有正有负，如果奖励为正，说明我们鼓励采取这种行为；如果奖励为负，说明我们不希望采取这种行为，本质是对采取这种行为的惩罚。
   奖励可以理解为是人与机械人进行交互的一种手段，通过奖励可以引导机械人按照我们的期望行事，实现我们的目标。奖励一定是依赖与当前状态和采取的行为的，是依据采取的行为给出的。

   在 gird-world 中，奖励的规则如下：

	1、如果机械人试图走出边界，则奖励reward=-1		
	2、如果机械人试图进入禁止的单元格，则奖励reward=-1	
	3、如果机械人到达目标单元格，则奖励reward=+1	
	4、其他情况，奖励reward=0	

   在强化学习中，用条件概率来表示采取行为获得的奖励。
$$p(r|s_i,a_n)：表示在状态s_i的条件下采取行为a_n获得奖励的概率$$
   以状态$s_1$为例（由于我们已经设计好了奖励规则，所以获得的奖励是确定的，但在实际情况中获得的奖励不是确定性的）： $p(r=-1|s_1,a_1)=1$

状态-行动-回报 trajectory

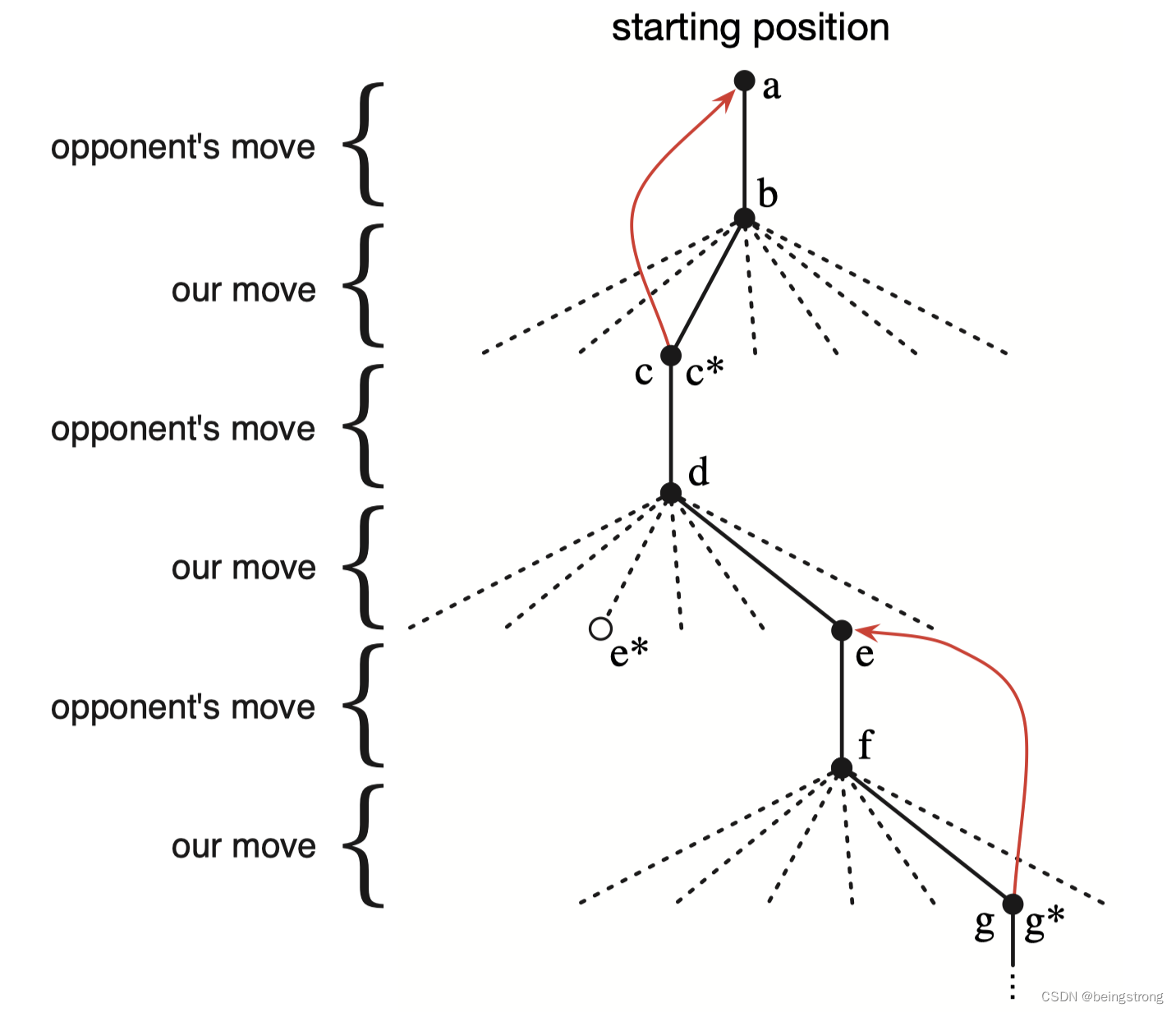
   在强化学习中，trajectory 是记录从起点到终点所采取的行为、获得的奖励，以及状态转移的链，包含了状态、奖励、行为三个变化。采样（return）是 trajectory 中很重要的概率，是针对一个 trajectory 而言，其作用是沿着一条trajectory 所得到的所有 奖励加起来。

.

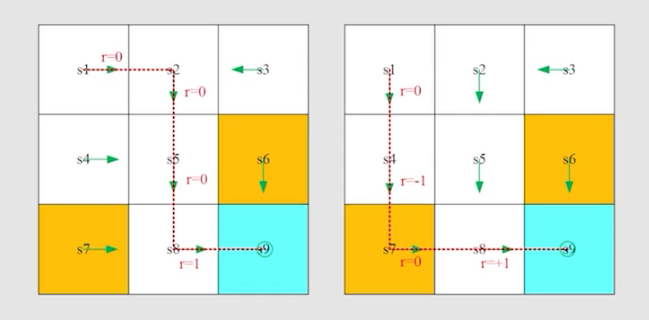
   如上图所示，不同的策略会得到不同的轨迹。那么，如何评估不同策略的优劣呢？在强化学习中，通常是使用 return 去评估一个策略的优劣。

衰减系数 $\gamma$ 的引入

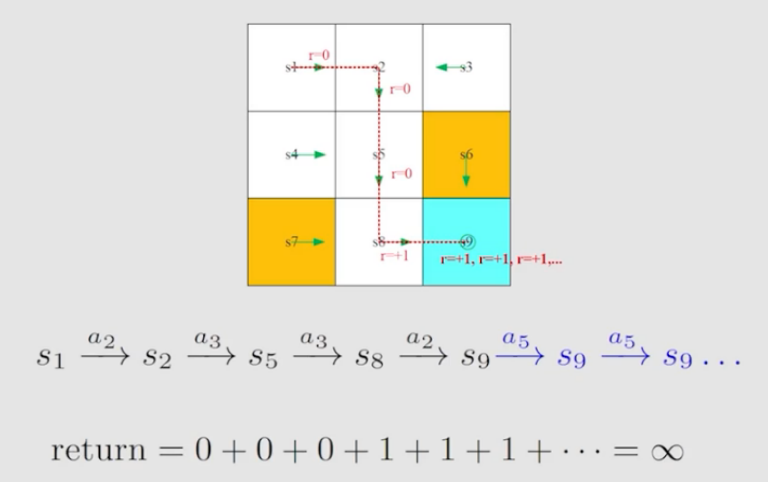
   如上图所示，当机械人到达终点时，策略还在进行，会持续反复进入终点，会使得return发散。为了解决这个问题，我们引入衰减系数(discount rate) $\gamma \in [0,1)$，引入衰减系数后会得到 discount return

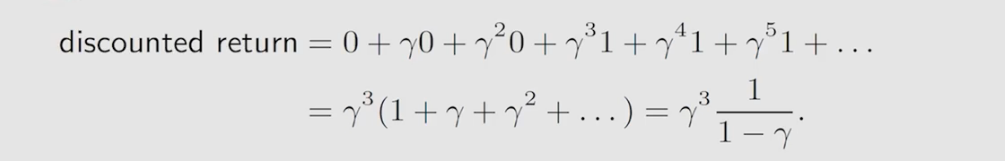
可以发现$\gamma$的作用：
   1、保证得到的奖励是有限的
   2、能够平衡遥期和近期的回报
    如果$\gamma$值偏小，则表明我们会更注重近期的奖励，即最终得到的奖励由最开始得到的奖励决定
    如果$\gamma$值偏大，则表明我们更注重长远的奖励，使机械人变得有远见

episode

   机械人按照策略与环境交互时，到达终点时机械人会停止，由此产生的轨迹被称为episode。
   在网格世界里，应该在到达目标后停下来吗？事实上，我们可以用一个统一的数学来处理。

马尔可夫决策过程MDP(Markov dwcision process)

   一个马尔科夫决策过程由三个要素组成：
1、集合：
$$状态集合：S$$$$行为集合：A(s)$$$$奖励集合：R(s,a)$$

2、概率：
$$状态转移概率：p(s^{\prime }|s,a)$$ $$奖励概率：p(r|s,a)$$

3、策略：
$$策略：\pi (a|s)$$

  马尔科夫性质：无后效性，指当前决策只与当前的状态及目标有关，与过去无关。

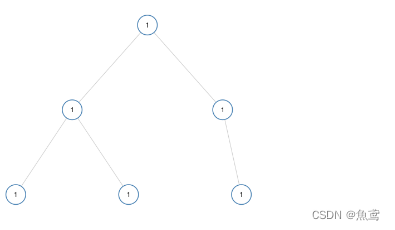
grid-world 网格世界可以抽象为一个更普遍的模型，即马尔可夫过程。圆圈表示状态，带有箭头的链接表示状态转移，马尔可夫决策过程一旦给出策略，就变成马尔可夫链。