《数据结构专栏》
文章目录
- 《数据结构专栏》
- 一、认识树结构
- 如何遍历树
- 如何创建一个树?
- 如何判断一颗树是否是完全二叉树?
- 二、树的简单算法——递归
- 1.相同树
- 2.镜像树
- 3.单值二叉树
- 总结
一、认识树结构
树的定义:树是指由N(N>=0)个有限结点组成的具有层次性关系的集合,是一种简单的非线性结构。当N=0时,称为空树。
如何遍历树
前序遍历
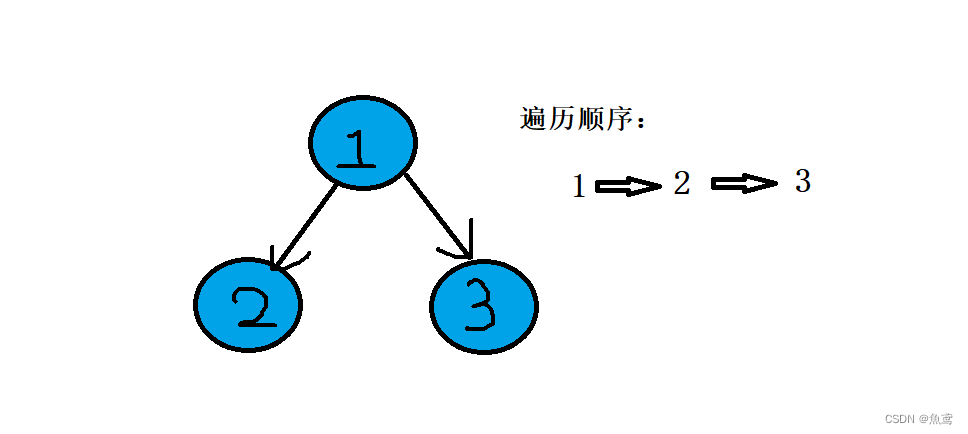
中序遍历
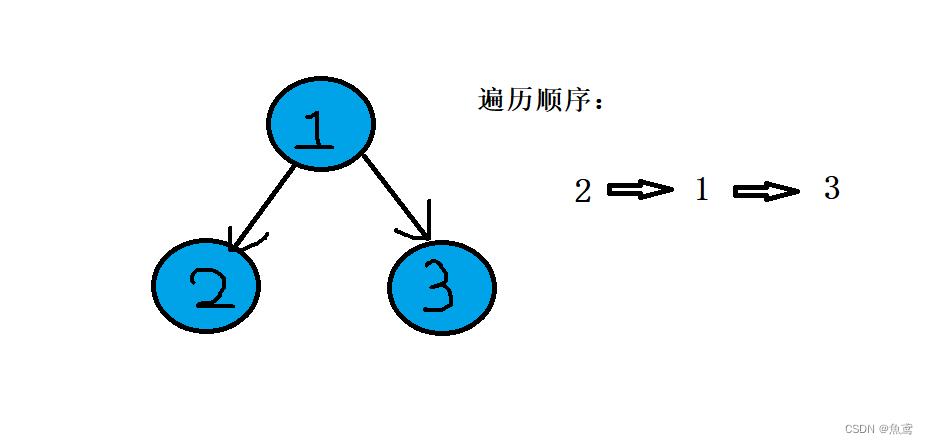
后序遍历
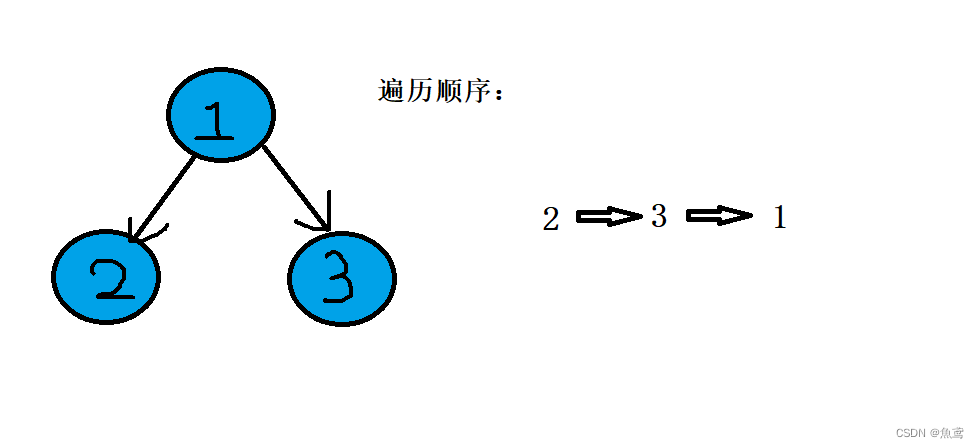
对于前中后序遍历使用的是根节点的位置决定前中序。
层序遍历
对于层序来说就是一层一层的进行遍历,由上面一层的根节遍历后带入下一层的节点数据。可以使用一个辅助队列的容器来实现对于层序遍历。
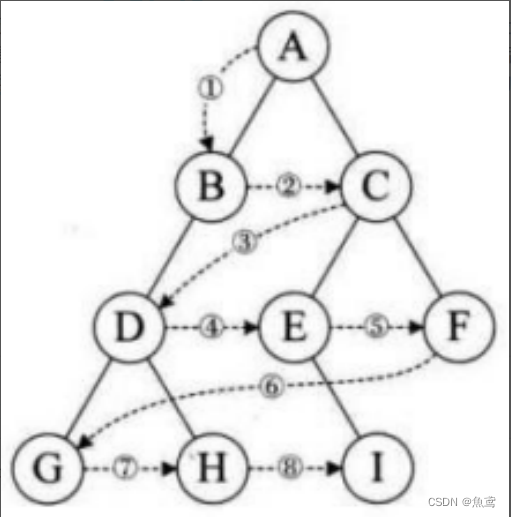
代码实现
//层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
Queue qu;
BTNode* cur;
QueueInit(&qu);
QueuePush(&qu, root);
while (! QueueEmpty(&qu))
{
cur = QueueFront(&qu);
putchar(cur->_data);
if (cur->_left)
{
QueuePush(&qu, cur->_left);
}
if (cur->_right)
{
QueuePush(&qu, cur->_right);
}
QueuePop(&qu);
}
QueueDestory(&qu);
}
如何创建一个树?
对于二叉树的遍历就是前、中、后序遍历。对于前序和后序遍历可以快速的找到根节点。然后通过中序分辨出左右子树。实现对于树的构建。
编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。 例如如下的先序遍历字符串: ABC##DE#G##F### 其中“#”表示的是空格,空格字符代表空树。建立起此二叉树以后,再对二叉树进行中序遍历,输出遍历结果。
输入:abc ## de #g ## f ###
输出:c b e g d f a
构建树
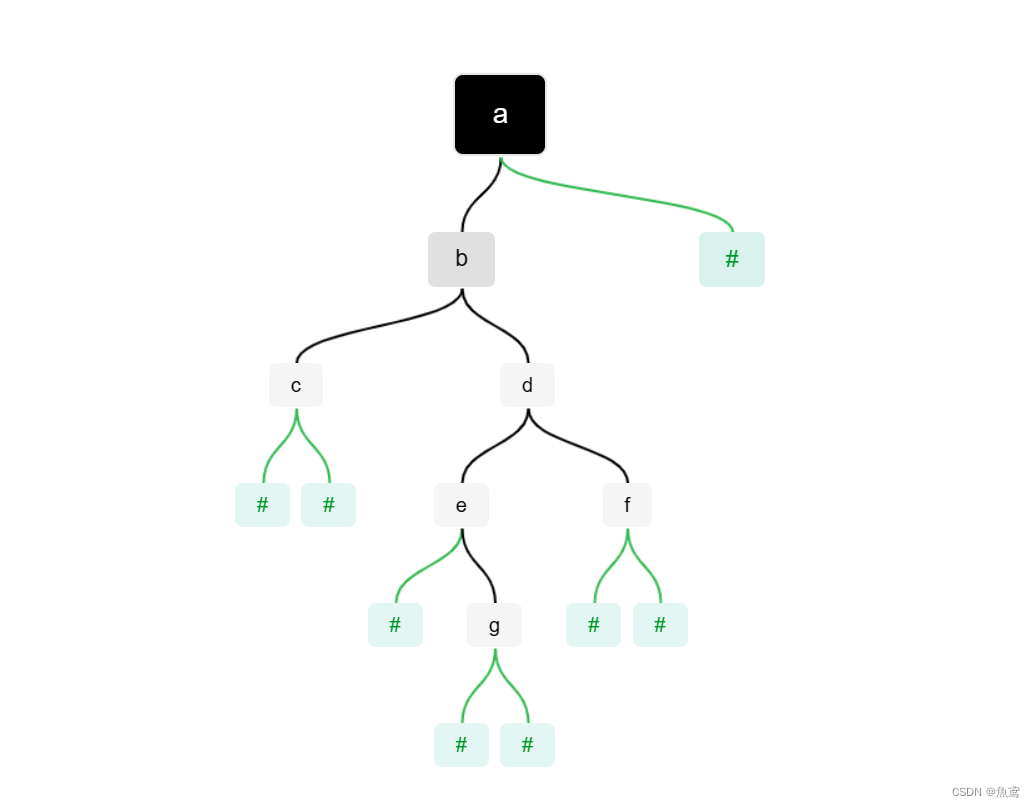
输入时是一个数组来进行数据存储的,所以在建立树的节点时就需要使用一个数据记录数组下标。
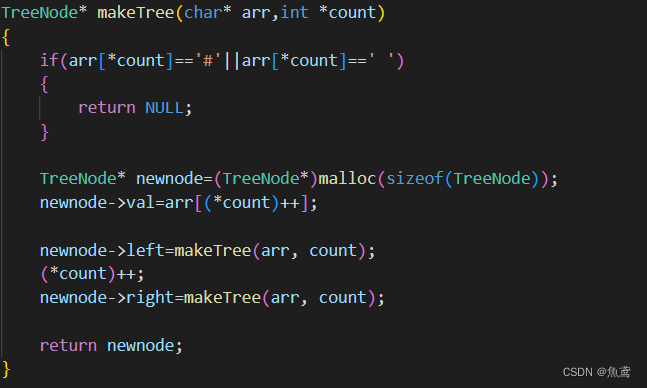
避免在递归时数组的下标使用后,返回下标重置,这里需要保持数组下标一致向后走,递归出来后才会对于整个数组遍历。使用的一个前序思想建树。
typedef struct TreeNode
{
struct TreeNode* left;
struct TreeNode* right;
char val;
}TreeNode;
TreeNode* makeTree(char* arr,int *count)
{
if(arr[*count]=='#'||arr[*count]==' ')
{
return NULL;
}
TreeNode* newnode=(TreeNode*)malloc(sizeof(TreeNode));
newnode->val=arr[(*count)++];
newnode->left=makeTree(arr, count);
(*count)++;
newnode->right=makeTree(arr, count);
return newnode;
}
void InOrder(TreeNode*root)
{
if(root==NULL)
return ;
InOrder(root->left);
printf("%c ",root->val);
InOrder(root->right);
}
int main()
{
char arr[101];
scanf("%s",arr);
int count=0;
TreeNode*tree=makeTree(arr, &count);
InOrder(tree);
return 0;
}
如何判断一颗树是否是完全二叉树?
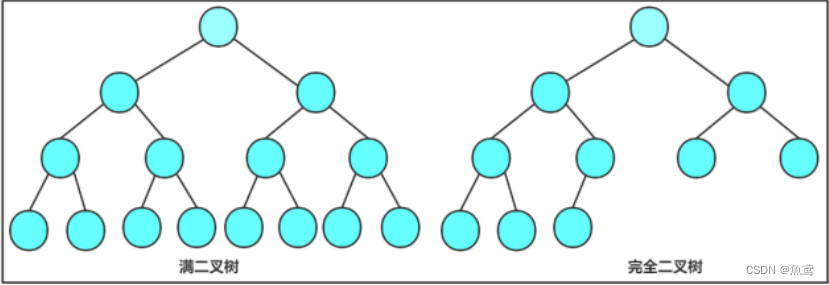
通过对于满二叉树和完全二叉树的对比发现完全二叉树的底层叶子结点数目是从左向右依次递减的,所以高度为n-1层的数目是不变的满二叉树一样,对于完全二叉树的最后一层进行分析即可。
对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对
于序号为i的结点有:
- 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
- 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
代码实现
int BinaryTreeComplete(BTNode* root)
{
Queue qu;
BTNode* cur;
int tag = 0;
QueueInit(&qu);
QueuePush(&qu, root);
while (! QueueEmpty(&qu))
{
cur = QueueFront(&qu);
putchar(cur->_data);
if (cur->_right && !cur->_left)
{
return 0;
}
if (tag && (cur->_right || cur->_left))
{
return 0;
}
if (cur->_left)
{
QueuePush(&qu, cur->_left);
}
if (cur->_right)
{
QueuePush(&qu, cur->_right);
}
else
{
tag = 1;
}
QueuePop(&qu);
}
BinaryTreeDestory(&qu);
return 1;
}
二、树的简单算法——递归
1.相同树
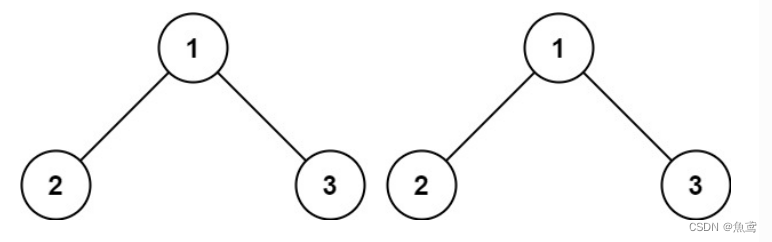
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。 如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的
对于题目讲解的相同理解应该是节点数据相同的数据,且左右子树结构也是相同的,对于空树的判断应该也要讨论,其中一颗树为空,另外一颗树不为空就明显不是相同的数。对于判断条件就是val值,左右子树结构,是否同时为空(判断是否都是叶子结点)。
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if(p==nullptr&&q==nullptr)return true;
if(p==nullptr||q==nullptr)return false;
if(q->val!=p->val)return false;
return isSameTree(q->left,p->left)&&isSameTree(q->right,p->right);
}
};
2.镜像树
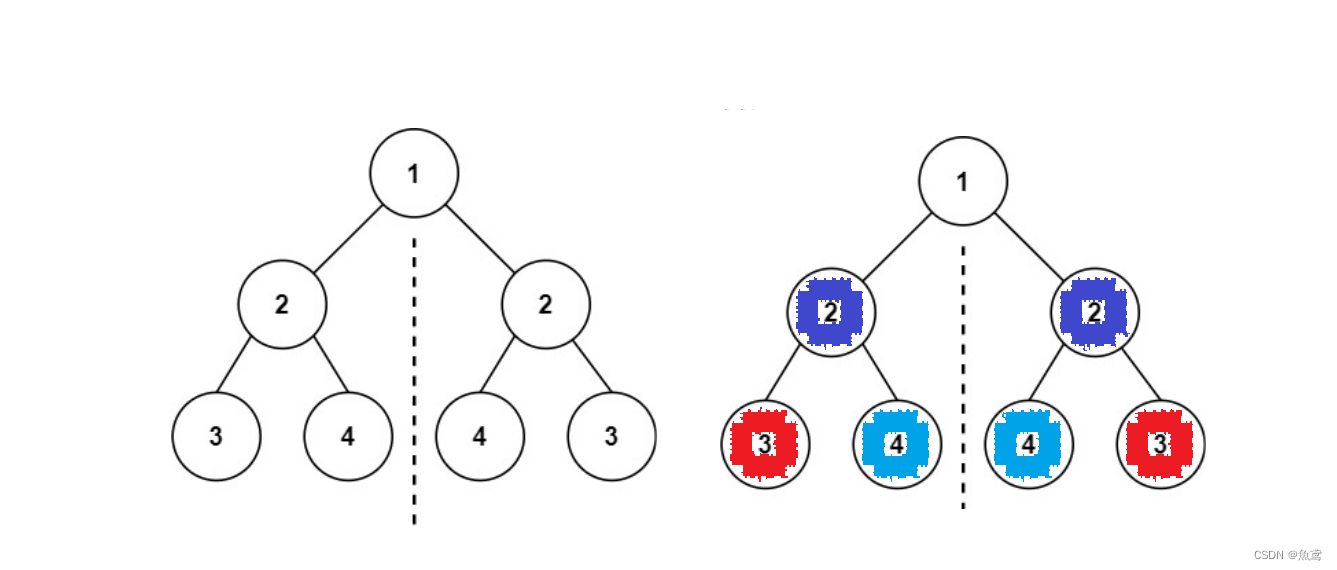
给你一个二叉树的根节点 root , 检查它是否轴对称
镜像树和解法有些类似于上面的相同树,但是又有些许差别就是对于树的结构比较他们是左子树和右子树的是对称的,使用的相同树的逻辑解题。
class Solution {
public:
bool issametree(TreeNode* root,TreeNode* subroot)
{
if(root==nullptr && subroot==nullptr)
{
return true;
}
if(root==nullptr || subroot==nullptr)
{
return false;
}
if(root->val==subroot->val)
{
return issametree(root->left,subroot->right) && issametree(root->right,subroot->left);
}
else
{
return false;
}
}
bool isSymmetric(TreeNode* root) {
if(root==nullptr) return true;
return issametree(root->left,root->right);
}
};
3.单值二叉树
题目:
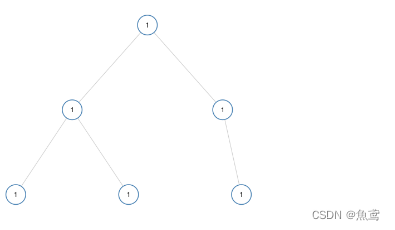
如果二叉树每个节点都具有相同的值,那么该二叉树就是单值二叉树。 只有给定的树是单值二叉树时,才返回 true;否则返回 false。
对于二叉树中值的查找值是一个比较常用的算法,使用深度遍历,从左子树到后面右子树依次遍历。不能使用节点数据相加后对比左右子树。会存在左边是多节点,右边只有一个节点数据。但是左右子树的值依旧相等。所以需要从根得va来比较判断左右子树。
class Solution {
public:
bool isUnivalTree(TreeNode* root) {
if(root==nullptr)return true;
if(root->left&&root->val!=root->left->val)
return false;
if(root->right&&root->val!=root->right->val)
return false;
return isUnivalTree(root->left)&&isUnivalTree(root->right);
}
};
总结
树的结构使用递归算法来进行遍历很容易理解,但是对于深度太深的树就会出现栈溢出情况。树用来存储数据显然不是一个很好的选择,容易出现歪脖子树,单只树。效率不高。可以进行后期优化成为搜索二叉树,AVL树……