原题链接：牛客网

题目内容：

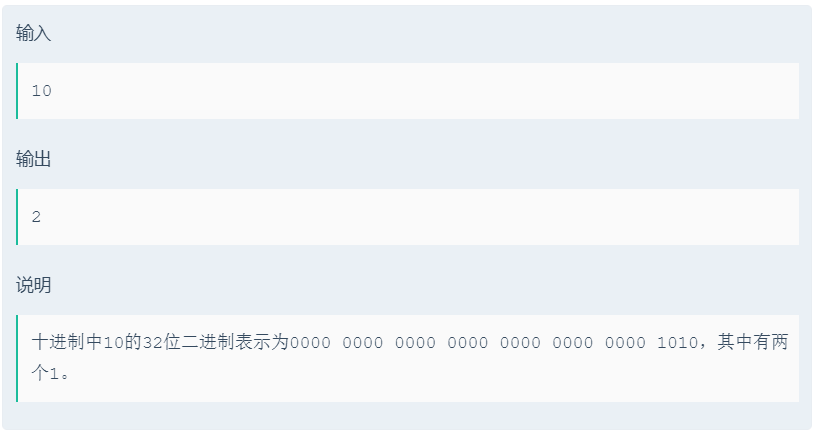
写一个函数返回参数二进制中 1 的个数，负数使用补码表示。

比如： 15    0000 1111    4 个 1

 

方法一：

#include<stdio.h>

int NumberOf1(unsigned int n)
{
	int count = 0;
	while (n)
	{
		if (n % 2 == 1)
			count++;
		n /= 2;
	}
	return count;
}

int main()
{
	int n;
	scanf("%d", &n);
	int num = NumberOf1(n);
	printf("%d\n", num);
}

NumberOf1函数的实现比较简单，它使用了一个循环，不断将n除以2，并判断余数是否为1。如果余数为1，则说明n的二进制表示中最低位为1，计数器count加1。然后，将n右移1位，继续进行下一轮循环，直到n的二进制表示中所有位都被访问过。最终，函数返回1的个数。

在main函数中，它调用了NumberOf1函数，读入一个整数n，并将它作为参数传递给NumberOf1函数。函数返回的结果被赋值给变量num，并通过printf函数将结果输出到控制台上。

方法二：

#include<stdio.h>

int NumberOf1(int n)
{
	int i = 0, count = 0;
	for (i = 0; i < 32; i++)
	{
		if ((n >> i) & 1 == 1)
			count++;
	}
	return count;
}

int main()
{
	int n;
	scanf("%d", &n);
	int num = NumberOf1(n);
	printf("%d\n", num);
}

NumberOf1函数的实现比较简单，它使用了一个for循环，对于n的二进制表示中的每一位进行检查。首先，将n右移i位，然后使用按位与运算符( &)判断n的第i位是否为1。如果为1，计数器count加1。最后，循环执行完毕后，函数返回统计到的1的个数。

需要注意的是，在统计有符号整数的二进制表示中1的个数时，应该考虑符号位的影响。如果使用带符号位的右移运算符(>>)，则符号位将被保留。因此，可以使用无符号位的右移运算符(>>)来消除符号位的影响。此外，在使用按位运算符( &)判断某一位是否为1时，也需要小心处理。

方法三：

#include<stdio.h>

int NumberOf1(int n)
{
	int count = 0;
	while (n)
	{
		n = n & (n - 1);
		count++;
	}
	return count;
}

int main()
{
	int n;
	scanf("%d", &n);
	int num = NumberOf1(n);
	printf("%d\n", num);
}

NumberOf1函数的实现比较巧妙，它使用了一个while循环和一种称为“Brian Kernighan算法”的技巧。循环中，不断对n与(n-1)进行按位与运算，这将会把n中最右边的1变为0。每次操作之后，计数器count加1，然后继续进行下一轮循环，重复这个过程，直到n为0。最终，函数返回1的个数。

使用Brian Kernighan算法来统计一个整数的二进制表示中1的个数的时间复杂度为O(log n)，比其他方法都要更加高效，因为它跳过了很多不必要的计算。该算法在处理大型数据集时效率尤其显著。