完全背包
文章讲解
视频讲解
有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将物品装入背包里的最大价值
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件
本题代码随想录上只有滚动 dp,不直观,下面我们还是 按照 0-1 背包滚动数组的推导过程,从二维 dp 开始推导。参考资料见此
还是从动态规划五部曲,从二维 dp 数组推导
例:
背包最大重量为4。
物品为:
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
每件物品都有无限个!
求解将物品装入背包能得到的最大价值
1、确定 dp 数组下标及值的含义
dp[i][j]:下标 i, j 表示从下标为 [0 - i] 的物品中任意取,放进容量为 j 的背包,dp[i][j] 的值表示从物品下标 [0 - i] 任取物品放进容量为 j 的背包所能装入的最大价值(每个物品可以取无限次)
2、确定递推公式
dp[i][j] 的值表示从下标为 [0 - i] 的物品中任取,放进容量为 j 的背包所能装入的最大价值,怎么求这个 dp[i][j] 呢?为了求 dp[i][j],肯定需要考虑从下标为 0 到 i 的物品中取物然后装进容量为 j 的背包的装取方案。得到这个 dp[i][j] 的装取方案有两种:一种是不放物品 i 就能得到最大价值,另一种是至少放一件物品 i 才能得到最大价值
- 不放物品 i:已经确定里面不放物品 i 的最大价值,为物品 0 到 i - 1 装进容量为 j 的背包的最大价值,即 dp[i - 1][j]
- 至少放一件物品 i:这个需要好好分析。至少放一件进去,则需要给背包预留一件物品 i 重量的位置,即最大价值应为 dp[][j - weight[i]] + value[i],这个表示“至少里面有一件物品 i ”。我们发现还有一个位置的下标没有确定,这个位置的下标含义是选择哪些物品去填充背包预留一个 weight[i] 后剩下的空间。因为是完全背包,就算已经有了一个物品 i,剩余的可用来填充剩余空间的物品范围也应该是 0 到 i,故最大价值为 dp[i][j - weight[i]] + value[i]
这两种装取方案中的最大值就是从物品 [0 - i] 任取物品放进容量为 j 的背包所能装入的最大价值,即递推公式:dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i])
注意这个递推公式的前提条件是背包要能装下物品 i,否则只需要考虑不放物品 i 的方案

3、dp 数组初始化
由递推公式,我们首先观察到 dp[i][j] 的值是由上一行(层)的值及本层靠左的值推出来的。
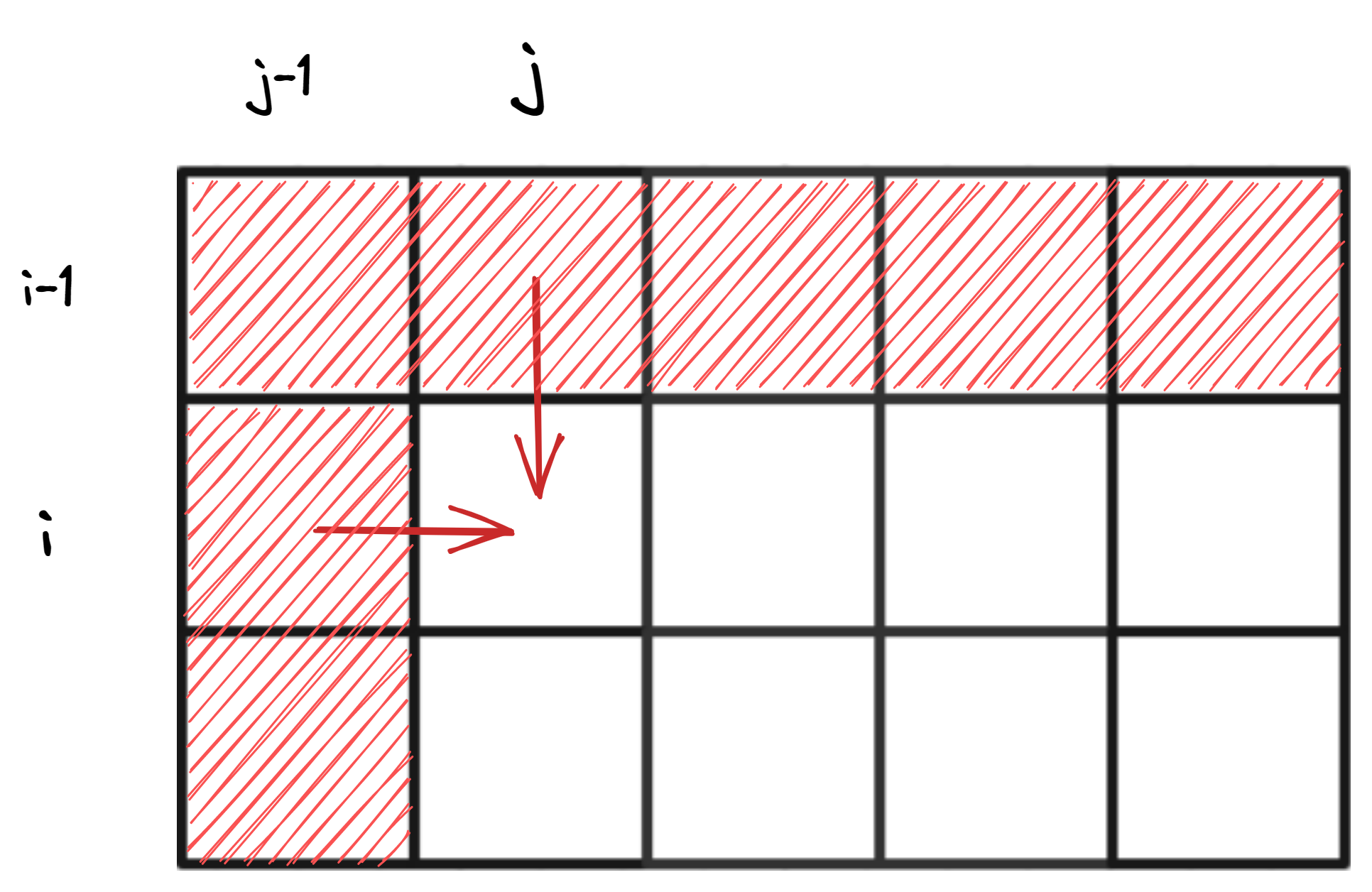
因此我们可以初始化 dp 数组第一行和第一列的值
初始化第一列,即初始化 dp[i][0],显然,根据 dp 数组下标及值的定义,将物品 0 到 i 装进容量为 0 的背包,啥也装不进去,能装的最大价值为 0

再来看看第一行,即初始化 dp[0][j],显然,根据 dp 数组下标 及值的定义,将物品 0 装进容量为 j 的背包,注意到可以装入多个物品 0,因此,容量 j 能装下 j / weight[0] 个物品 0,其能装下的最大价值就是 j / weight[0] * value[0]
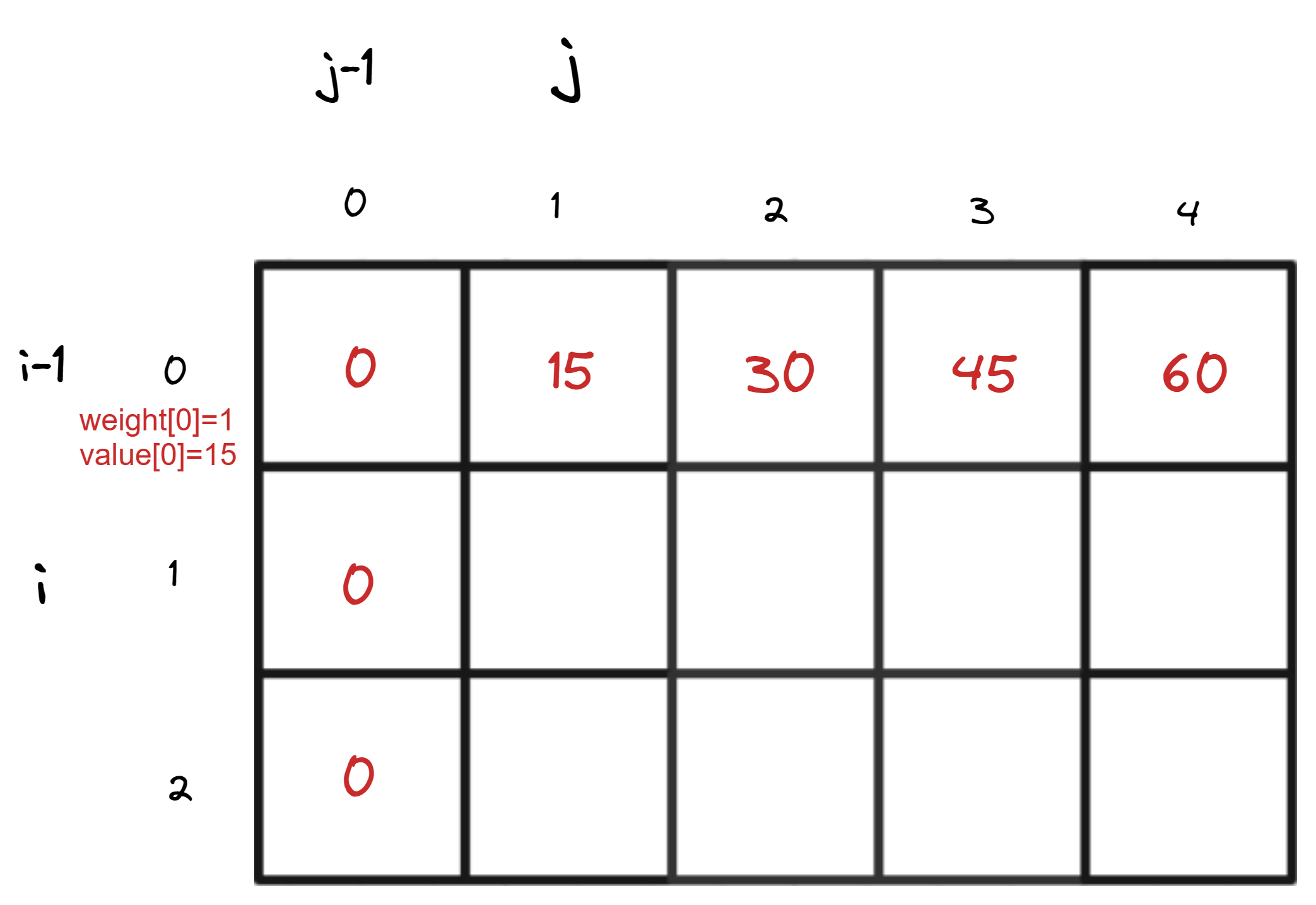
其他位置随意初始化,反正都会被遍历覆盖
4、确定遍历顺序
可以从上层(上一行)遍历填充到下层(下一行),然后单层中从左遍历填充向右。因为某个位置的值是由上一行(层)的值及本层该位置靠左的值推出来的。只要保证该位置靠上和靠左位置的值是更新后的正确的值
代码中,外层 for 循环遍历物品 i 即可(一个物品的索引代表一行,一行一行遍历,每行从左向右遍历)
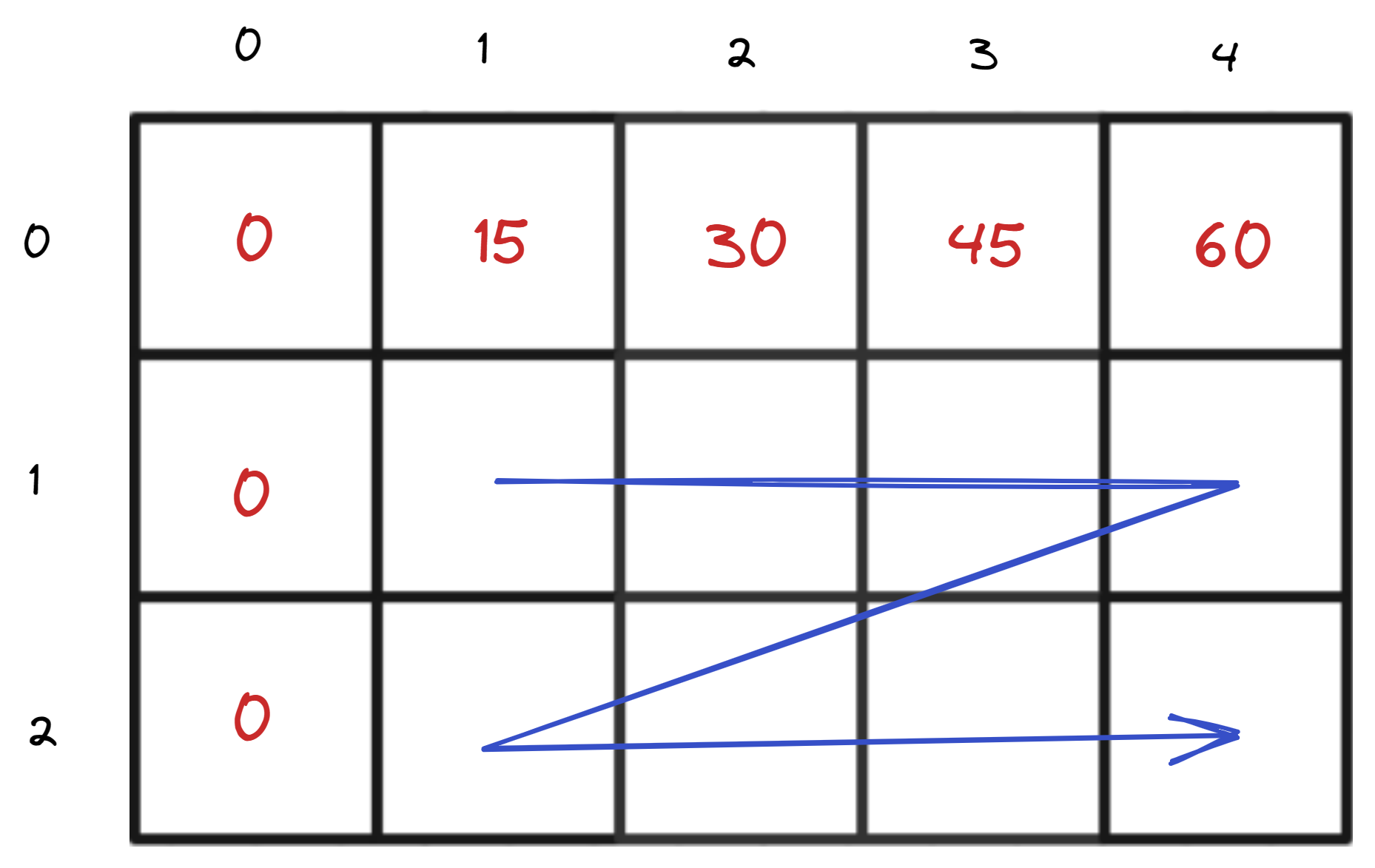
5、打印 dp 数组验证
代码如下
void bag_problem_2d() {
cout << "请输入背包容量:";
int bagSize;
cin >> bagSize;
cout << "请输入物品个数:";
int n;
cin >> n;
cout << "请依次输入物品重量:" << endl;
vector<int> weight(n);
for (int i = 0; i < n; ++i) {
cin >> weight[i];
}
cout << "请依次输入物品价值:" << endl;
vector<int> value(n);
for (int i = 0; i < n; ++i) {
cin >> value[i];
}
cout << endl;
cout << "背包容量:" << bagSize << endl;
cout << "物品重量:";
for (auto i : weight)
cout << i << "\t\t";
cout << endl;
cout << "物品价值:";
for (auto i : value)
cout << i << "\t\t";
cout << endl << endl;
// 定义dp数组下标及含义:dp[i][j]:从物品0到i中任取,放进容量为bagSize的背包,得到最大价值为dp[i][j]。每个物品可无限次放入
vector<vector<int> > dp(n, vector<int>(bagSize + 1, 12345)); // 12345表示其他位置随意初始化都行
// 递推公式:dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i])
// 初始化:初始化第一行和第一列
for (int j = 0; j <= bagSize; ++j) {
dp[0][j] = (j / weight[0]) * value[0]; // j / weight[0] 表示容量为j的背包能装下物品0的个数
}
for (int i = 0; i < n; ++i) {
dp[i][0] = 0; // 容量为0的背包无法装下物品,能装下的最大价值为0
}
// 遍历填充dp数组:一行一行,从左向右填充
for (int i = 1; i < n; ++i) // 遍历物品(即遍历每一行),第一行已经被初始化了,从第二行开始遍历填充
for (int j = 1; j <= bagSize; ++j) // 遍历背包(遍历行中的元素),第一列已经被初始化了,从第二列开始遍历填充
{
if (j >= weight[i])
dp[i][j] = max(dp[i-1][j], dp[i][j-weight[i]]+value[i]);
else
dp[i][j] = dp[i-1][j];
}
// 打印dp数组验证
cout << "dp数组如下:" << endl;
for (const auto & line : dp) {
for (const auto item : line)
cout << item << "\t\t";
cout << endl;
}
return;
}完全背包:滚动数组
回顾一下二维的递推公式(前提是背包要能装下物品 i)
dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i])还是之前 0-1 背包的思路,我们能不能只维护一层的数据?
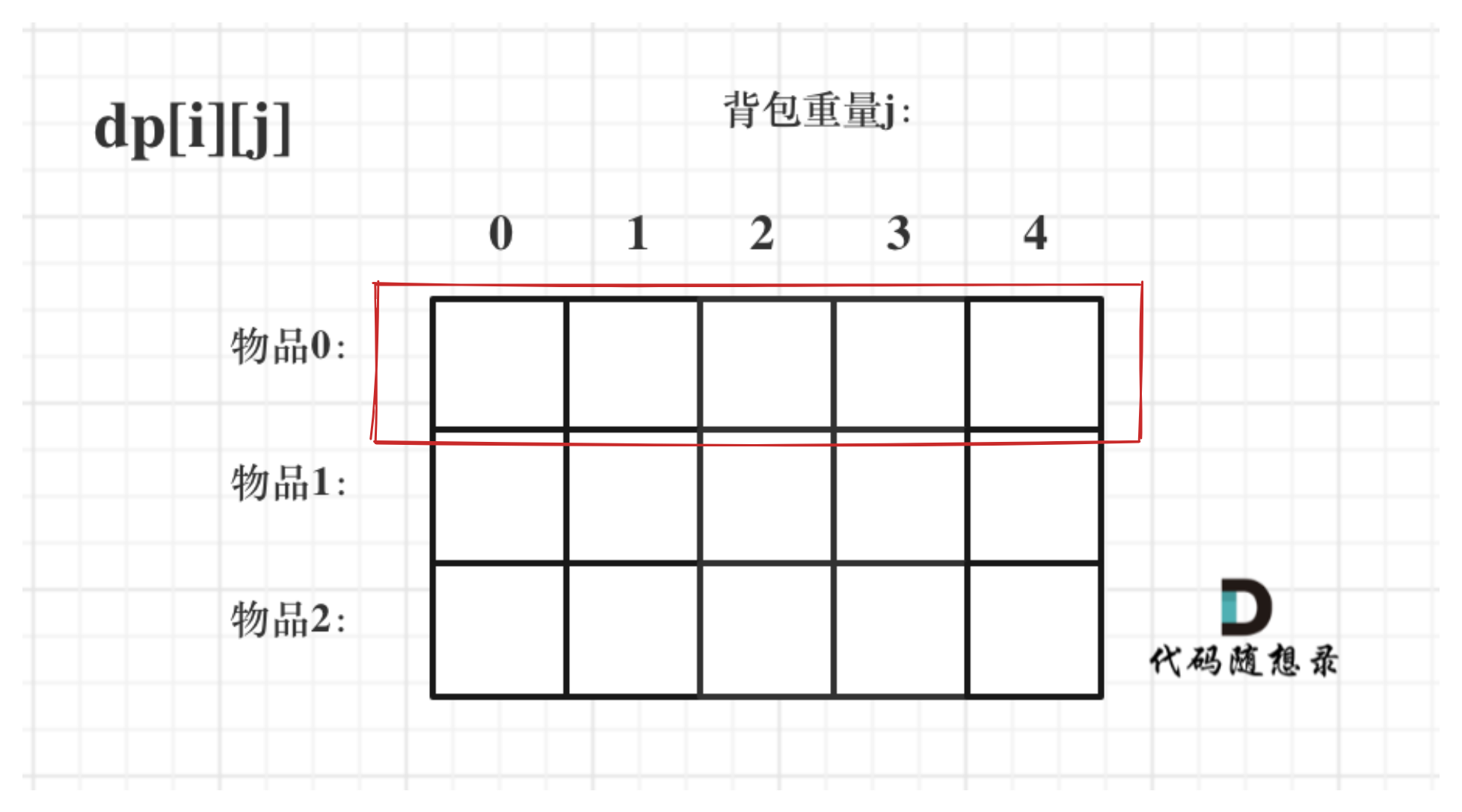
先看看压缩后的递推公式:因为状态压缩了,dp 数组变成了一维,下标 j 代表背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);居然和 0-1 背包的滚动数组递推公式一样了,但是其实含义是不一样的
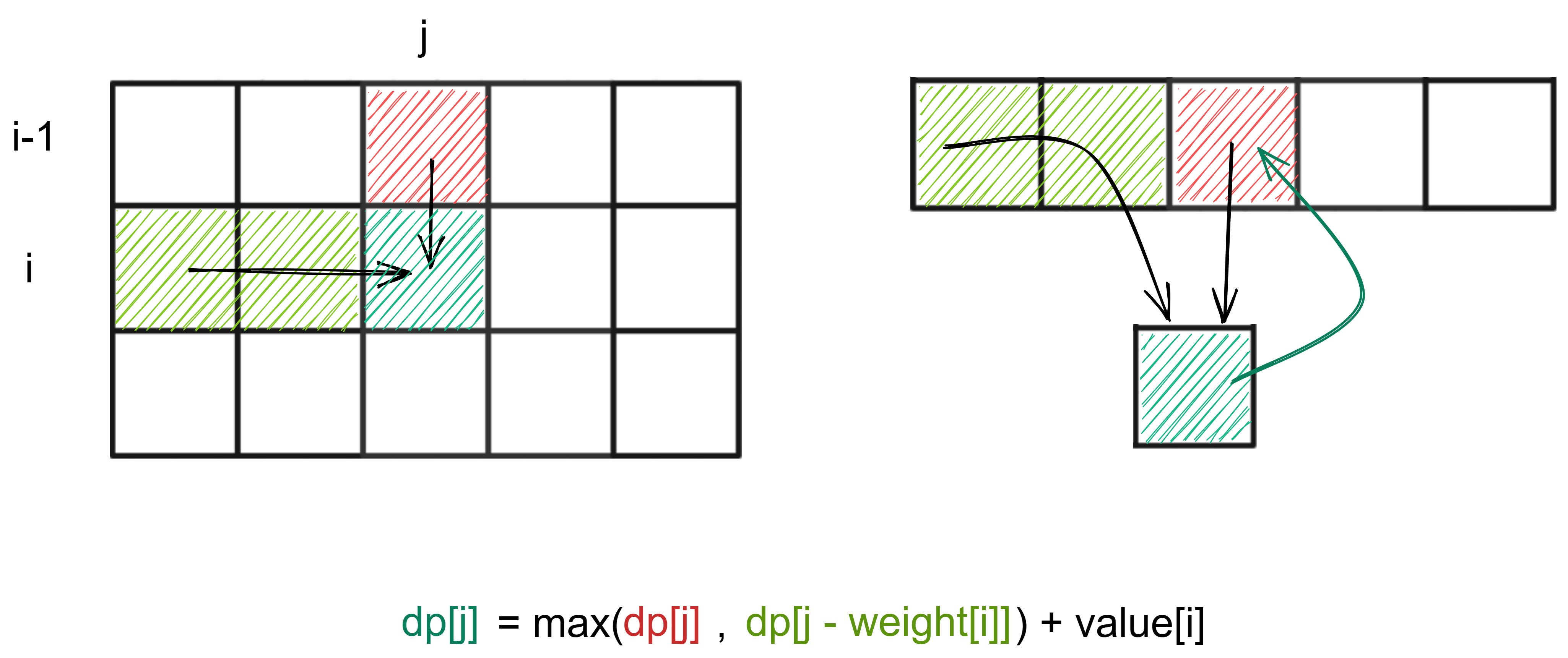
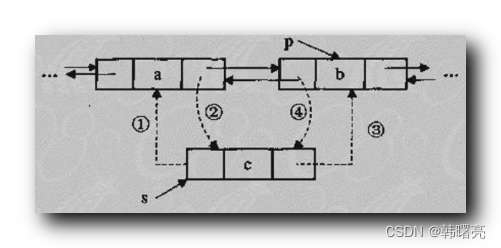
左图为原二维 dp 数组,右图是我们压缩后的滚动数组
在二维 dp 数组中,我们求某一个位置(青色)的 dp 值,依赖的是当前位置上一层元素(红色)及当前位置左边元素的值(浅绿色)
映射到滚动数组中,我们求某一个位置(青色)的 dp 值,依赖的是当前位置元素的旧值(红色)及当前位置左边元素的值(浅绿色)
我们从图中可以看出几个关键点
- 因为滚动数组维护的是某一层二维 dp 数组的数据,为了实现一层一层遍历填充,外层 for 循环为物品 i,表示在二维数组中需要一层一层填充,每遍历完一轮外层的循环,表明更新完了一层二维 dp 数组
- 滚动数组的最左边首个元素,对应的是原二维 dp 数组每层的第一列元素,其值是背包容量为 0 时装入物品的最大价值,应该始终为 0
- 更新每层中的元素时,即更新我们的一维滚动数组时,需要从左向右遍历填充!因为二维数组中我们更新当前层某位置元素依赖的是其正上方元素及其左边的元素(看图),对应到滚动数组中,更新某位置元素依赖的是当前位置的旧值及当前位置左边元素的值(看图)。而浅绿色部分的值是当前层元素,在当前层已被更新了新值,故在滚动数组中,为了保证浅绿色部分(即待更新元素左边元素)是已经在当前层被更新的正确值,需要从左向右遍历
总结一下就是,完全背包的滚动数组代码实现和 0-1 背包的滚动数组代码实现只有两个区别:
- 完全背包滚动数组只需要关注最左边第二个元素及其后面的值,因为其首个元素始终为 0 (有人会说,那 0-1 背包第一列不也是啥都装不进去的情况,为啥还需要一直更新?答:因为 0-1 背包有些题目可能会出现重量为 0 的物品,那就能装进去该物品了;而完全背包如果出现重量为 0 的物品,那就能猛猛无限装这个物品,就乱套了,所以完全背包问题不会有重量为 0 的物品,所以其背包容量为 0 的时候,不可能装入物品)
- 完全背包滚动数组内层遍历背包容量的顺序是从左向右正序遍历,而 0-1 背包滚动数组内层遍历背包容量的顺序是从右向左倒序遍历(根本原因是:相同的递推公式具有不同的含义。0-1 背包中,倒序遍历的原因是不覆盖滚动数组维护的上一层二维 dp 数组的有用数据;完全背包中,正序遍历的原因是需更新滚动数组维护的当前层二维 dp 数组的有用数据)
代码如下
void bag_problem_1d() {
cout << "请输入背包容量:";
int bagSize;
cin >> bagSize;
cout << "请输入物品个数:";
int n;
cin >> n;
cout << "请依次输入物品重量:" << endl;
vector<int> weight(n);
for (int i = 0; i < n; ++i) {
cin >> weight[i];
}
cout << "请依次输入物品价值:" << endl;
vector<int> value(n);
for (int i = 0; i < n; ++i) {
cin >> value[i];
}
cout << "背包容量:" << bagSize << endl;
cout << "物品重量:";
for (auto i : weight)
cout << i << "\t\t";
cout << endl;
cout << "物品价值:";
for (auto i : value)
cout << i << "\t\t";
cout << endl << endl;
// 定义状态压缩后的dp数组
vector<int> dp(bagSize + 1);
// 递推公式:dp[j] = max(dp[j], dp[j-weight[i]]+value[i])
// 初始化:初始化第一行,i=0那一行,目前dp的值就是第一行
for (int j = 0; j <= bagSize; ++j) {
dp[j] = j / weight[0] * value[0]; // 容量为 j 的背包能装物品0的个数乘物品0的价值
}
// 打印一下第一行的dp数组值
for (auto item : dp)
cout << item << "\t\t";
cout << endl;
// 遍历填充dp数组:一行一行填充
for (int i = 1; i < weight.size(); ++i) // 遍历物品(一层一层遍历,第一行已经被初始化了,从第二行开始)
{
for (int j = 1; j <= bagSize; ++j) // 遍历背包(正序遍历,且从第二个元素遍历,因为首个元素(二维数组第一列)始终为0)
{
if (j >= weight[i]) // 当能装下物品i才装
dp[j] = max(dp[j], dp[j-weight[i]]+value[i]);
// else // 装不下物品i
// dp[j] = dp[j];
}
// 遍历完了一轮外层循环,我们打印看看这层dp数组
for (auto item : dp)
cout << item << "\t\t";
cout << endl;
}
return;
}518.零钱兑换 II
力扣题目链接/文章讲解
视频讲解
这是一道典型的背包问题,一看到钱币数量不限,就知道这是一个完全背包
将硬币看成物品,面额看成物品重量,总金额代表背包容量
此时问题就转化为,装满容量为 bagSize 的背包,有几种方法,每个物品可以无限次取
但本题和纯完全背包不一样,纯完全背包是凑成背包最大价值是多少,而本题是要求装满背包的方法数
所以,又得开始推二维 dp,进一步拓展到滚动 dp 了(心累)
动态规划五部曲,来吧!!!!!!!!
1、确定 dp 数组下标及值的含义
dp[i][j]:下标 i, j 表示从下标为 [0 - i] 的物品中任意取,装满容量为 j 的背包,dp[i][j] 的值表示从物品下标 [0 - i] 任取物品装满容量为 j 的背包有多少种方法

2、确定递推公式
dp[i][j] 的值表示从下标为 [0 - i] 的物品中任取(每个物品能取多次),装满容量为 j 的背包的方法数,怎么求这个 dp[i][j] 呢?为了求 dp[i][j],肯定需要考虑从下标为 0 到 i 的物品中取物然后装满容量为 j 的背包的装入方案。得到这个 dp[i][j] 的方案有两种:一种是不放物品 i 装满了背包,另一种是至少放了一件物品 i 装满了背包
- 不放物品 i:已经确定里面不放物品 i 的装入方法数,为物品 0 到 i - 1 装满容量为 j 的背包的方法数,即 dp[i - 1][j]
- 至少放一件物品 i:至少放一件进去,则首先需要给背包预留一件物品 i 重量的位置,即剩余容量为 j - weight[i],下一步还需要从 0 到 i 选择物品去填充背包的剩余容量(因为是完全背包,物品 i 能被多次选择)。故这种情况下装满容量为 j 的背包的方法数为 dp[i][j - weight[i]]
这两种方案各自方法数加起来就是总的装满容量为 j 的背包的方法数,即递推公式:dp[i][j] = dp[i - 1][j] + dp[i][j - nums[i]]
注意这个递推公式的前提条件是背包要能装下物品 i,否则只需要考虑不放物品 i 的方案
3、dp 数组初始化
由递推公式,我们首先观察到 dp[i][j] 的值是由上一行(层)的值及本层靠左的值推出来的。

因此我们可以初始化 dp 数组第一行和第一列的值
先看第一列:用物品 j 装满容量为 0 的背包的方法数为 1:不装入即可
for (int i = 0; i < weight.size(); ++i)
{
dp[i][0] = 1; // 装满容量为0的背包:1种方法
}再看第一行:用物品 0 装满容量为 j 的背包的方法数:当容量 j 为物品重量的整数倍,则有一种方案能装满,否则无法装满
for (int j = 1; j <= bagSize; ++j)
{
if (j % weight[0] == 1) dp[0][j] = 0; // 无法装满
if (j % weight[0] == 0) dp[0][j] = 1; // 容量为物品0重量整数倍,能装满
}其余位置随意初始化,反正都会被遍历覆盖
4、确定遍历顺序
可以从上层(上一行)遍历填充到下层(下一行),然后单层中从左遍历填充向右。因为某个位置的值是由上一行(层)的值及本层该位置靠左的值推出来的。只要保证该位置靠上和靠左位置的值是更新后的正确的值
代码中,外层 for 循环遍历物品 i 即可(一个物品的索引代表一行,一行一行遍历,每行从左向右遍历)
5、打印dp数组验证
代码如下
class Solution {
public:
int change(int amount, vector<int>& coins) {
// amount为背包容量,coins为物品
// 定义dp数组下标及值的含义:dp[i][j]下标表示从物品0到i任取放满容量为j的背包,装满背包的方法数为dp[i][j]
vector<vector<int> > dp(coins.size(), vector<int>(amount + 1));
// 递推公式:dp[i][j] = dp[i-1][j] + dp[i][j-coins[i]]
// 初始化dp第一列
for (int i = 0; i < coins.size(); ++i) {
dp[i][0] = 1; // 装满容量为0的背包:1种方法
}
// 初始化dp第一行,第一行的第一个已经被初始化为1了
for (int j = 1; j <= amount; ++j) {
if (j % coins[0] == 1) dp[0][j] = 0; // 无法装满
if (j % coins[0] == 0) dp[0][j] = 1; // 容量为物品0重量整数倍,能装满
}
// 遍历填充:从上往下,从左往右
for (int i = 1; i < coins.size(); ++i) // 第一行已经被初始化了,从第二行开始
for (int j = 1; j <= amount; ++j) { // 第一列已经被初始化了,从第二列开始
if (j >= coins[i]) // 容量为j的背包能放下物品i
dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i]];
else // 放不下物品i,则只考虑不放物品i
dp[i][j] = dp[i - 1][j];
}
return dp[coins.size() - 1][amount];
}
};同样,这道题能够利用滚动 dp 数组优化
递推公式如下
dp[j] = dp[j] + dp[j - coins[i]]二维 dp 中,当前层某位置的 dp 值由其上一层对应位置的 dp 值与当前层该位置左边(已在当前层更新) 的dp 值推出
对应到滚动数组中,某位置的 dp 值由该位置的旧值与该位置左边(已在当前层更新)的 dp 值推出
代码如下
class Solution {
public:
int change(int amount, vector<int>& coins) {
// amount为背包容量,coins为物品
// 定义dp数组下标及值的含义:dp[j]下标表示取物品放满容量为j的背包,装满背包的方法数为dp[j]
vector<int> dp(amount + 1);
// 递推公式:dp[j] = dp[j] + dp[j-coins[i]]
// 初始化原二维dp数组第一行
for (int j = 0; j <= amount; ++j) {
if (j % coins[0] == 1) dp[j] = 0; // 无法装满
if (j % coins[0] == 0) dp[j] = 1; // 容量为物品0重量整数倍,能装满
}
// 遍历填充:先遍历物品(表示一层一层遍历)
for (int i = 1; i < coins.size(); ++i) // 二维dp的第一行已经被初始化了,从第二行开始
for (int j = 1; j <= amount; ++j) { // 二维dp的第一列已经被初始化了,从第二列开始。注意正序,保证该层该位置左侧的元素是已在当前层被更新的有效值
if (j >= coins[i]) // 容量为j的背包能放下物品i
dp[j] = dp[j] + dp[j - coins[i]];
else // 放不下物品i,则只考虑不放物品i
dp[j] = dp[j];
}
return dp[amount];
}
};377.组合总和 Ⅳ
力扣题目链接/文章讲解
视频讲解
本题要考虑排序!
本题虽然在完全背包章节,但是因为非常规,按照完全背包的思路一步一步走不太好想
直接用动态规划五部曲推导
1、定义 dp 数组下标及值的含义
dp[j]:j 表示排列中的元素之和等于 j, dp[j] 的值为排列方案数
2、确定递推公式
考虑排列的最后一个元素。“最后一个”暗藏我们考虑到了排列应有的顺序特性
假设该排列的最后一个元素是 i,对于元素之和等于 j − i 的每一种排列,在最后添加 i 之后即可得到一个元素之和等于 j 的排列,因此在计算 dp[j] 时,应该计算所有的 dp[j - i] 之和,即 dp[j] += dp[j - i]。(前提 j 大于等于 i)
3、dp 数组初始化
dp[0] = 1,表示只有当不选取任何元素时,元素之和才为 0,因此只有 1 种方案
因为其他位置要用 dp 做累加,故其他位置初始化为0
4、确定遍历顺序
因为 dp[j] 的值依赖于其左边的 dp 值,从左向右遍历,保证待求位置的左边的 dp 值为更新过的正确值
5、打印 dp 数组验证
代码如下
class Solution {
public:
int combinationSum4(vector<int>& nums, int target) {
vector<unsigned long long> dp(target + 1, 0);
dp[0] = 1; // 初始化
for (int j = 1; j <= target; ++j) {
for (const auto & i : nums) { // 计算dp[j]时,需要计算所有dp[j-i]的和
if (j >= i)
dp[j] += dp[j - i]; // 前提是j>=i
}
}
return dp[target];
}
};本题没用完全背包的思考过程,反而更简单
回顾总结
滚动数组的详细推导思考起来太复杂,可以直接记忆下面的一下小技巧
- 常规完全背包常规 0-1 背包相比,最大的区别在于:滚动数组时,完全背包内层遍历背包容量的顺序从左向右不用逆序
- 一般来说,求方案数的递推公式都是 dp[j] += dp[j - w[i]],不过含义有所区别,因此别的代码细节应该做相应修改