前面讨论的方差是 一维随机变量X,    对于二维随机变量， 怎样计算方差呢？

这就引出了 协方差： 讨论X与Y之间相互关系的数字特征。 

一   协方差的定义

协方差通俗的理解： 两个随机变量X,  Y协作产生的方差。

计算协方差的公式有：Cov(X , Y)  = E(XY) - E(X)E(Y)

就是说，

协方差＝ 乘积的期望 － X、Y各自期望的乘积

当X=Y时，                  Cov(X,  X) = D(X)

二  协方差的性质

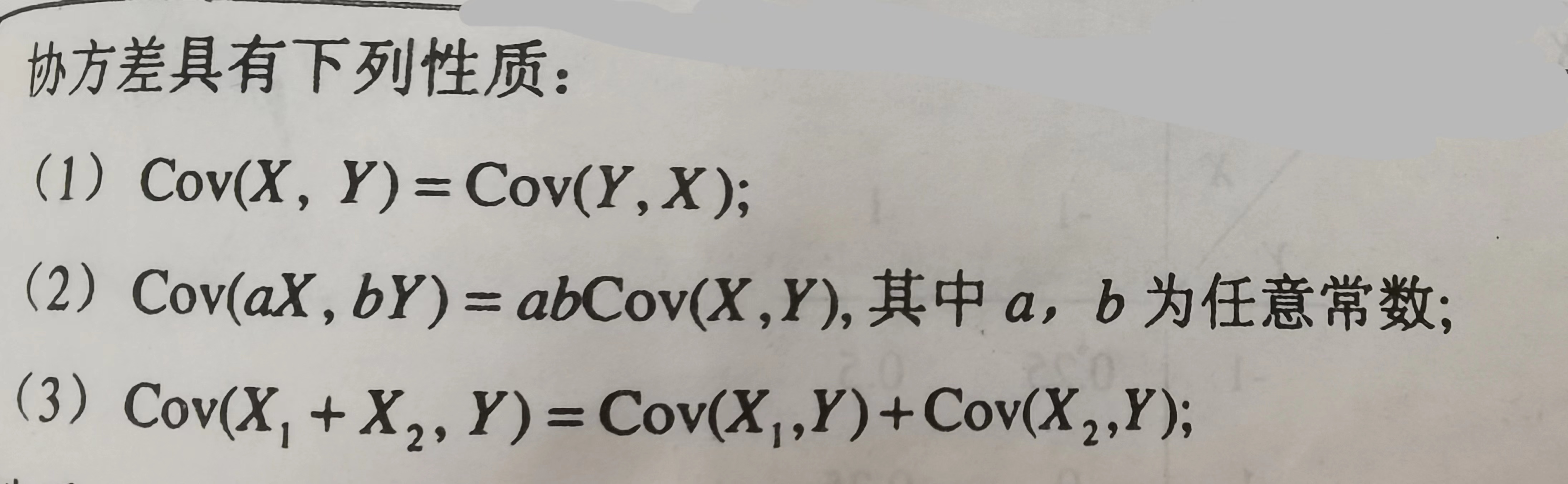
（5）Cov(X, n-X) = Cov(X, n) — Cov(X, X)。

注意： 常数跟随机变量的协方差=0， 因为两者是独立的。 

~~~~~~~~~~~~~~

三  相关系数的定义

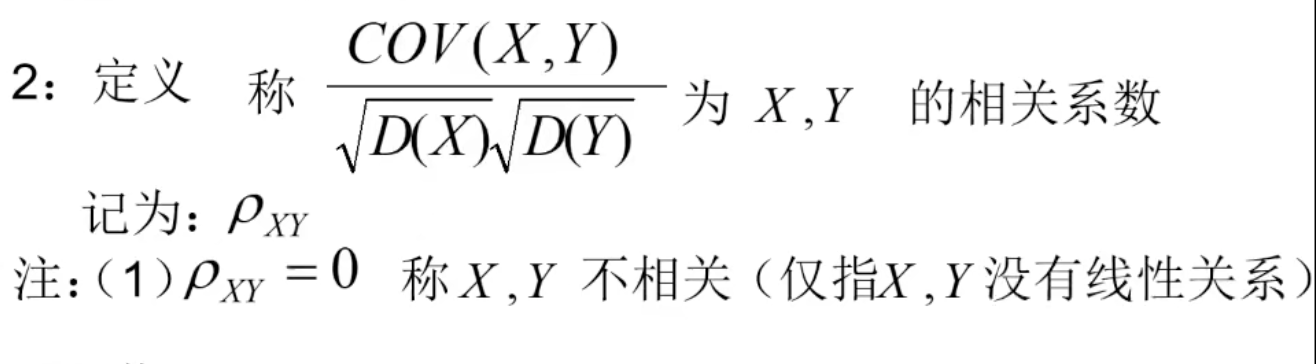
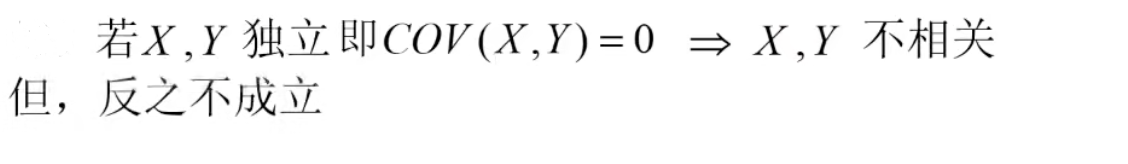
四   相关系数 的性质

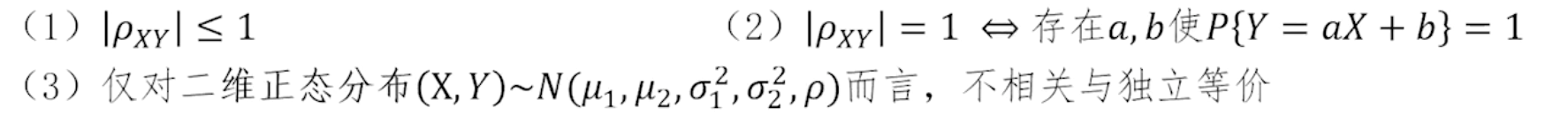
相关系数是两个随机变量间线性联系密切程度的度量。当 ρᵪᵧ =0 时，X与Y之间无线性关系。当

|ρᵪᵧ| =1 时，X与Y存在完全的线性关系。

（4）当D(X)>0, D(Y)>0时，  随机变量X与Y 不相关的充分必要条件是Cov(X, Y) = 0. 

 若X与Y相互独立，则Cov(X, Y) =0,  因此X与Y不相关。 反之X与Y不相关，但不一定相互独立。

五 看例题

题1  ρᵪᵧ = 0.9， M = X-0.4,  ρᵧ៳ = _____.

解： Cov(Y, M) = Cov(Y,  X-0.4) = Cov(Y,X),

因为Cov(Y, X-0.4) = Cov(Y, X) - Cov(Y, 0,4) , Cov(Y, 0.4)=0.

又有， D(M) = D(X-0.4) = D(X).   

所以 ρᵧ៳ = 0.9。 此题结果简单， 有没有快速方法呢？  实际上我们用瞪眼法， 可以得出结果。

因为X, Y线性相关度为0.9，即90%, M=X-0.4 说明M，X 是完全的线性相关，仅仅移位了0.4，所以Y, M的线性相关度为0.9。