第1关:硬币实验
任务描述
本关任务:计算机产生的伪随机数来模拟抛硬币试验。
相关知识
为了完成本关任务,你需要掌握:1.如何获取数组的长度,2.如何遍历数组。
随机数
随机数在随机化算法设计中扮演着十分重要的角色。 在现实计算机上无法产生真正的随机数,因此在随机化算法中使用的随机数都是一定程度上随机的,即伪随机数。
用计算机产生的伪随机数来模拟抛硬币试验。 假设抛10次硬币,每次抛硬币得到正面和反面是随机的。拋10次硬币构成一个事件。 调用Random(2)返回一个二值结果。 在主程序中反复调用函数TossCoins模拟拋10次硬币这一事件50000次。 用head[i](0<=i<=10)记录这50000次模拟恰好得到i次正面的刺手。最终输出模拟抛硬币事件得到的正面事件的概率图。
编程要求
根据提示,在右侧编辑器补充代码。
测试说明
RandomNumber.h 函数已经写好,可以点击查看。
平台会对你编写的代码进行测试: 例如: 输入: 10 50000 输出:
0 *1 *2 *3 *4 *5 *6 *7 *8 *9 *10 *`
开始你的任务吧,祝你成功!
参考答案:
#include "RandomNumber.h"
#include <iostream>
using namespace std;
int TossCoins(int numberCoins);
int main()
{
//模拟随机抛硬币事件
int NCOINS;
long NTOSSES;
cin >>NCOINS;
cin >>NTOSSES;
//heads[i]是得到i次正面的次数
long i,heads[NCOINS+1];
int j,position;
//初始化数组heads
for(int j=0; j<NCOINS+1;j++)
{
heads[j] = 0;
}
//重复50,000次模拟事件
for(int i=0; i<NTOSSES; i++)
{
heads[TossCoins(NCOINS)]++;
}
//输出频率图
for(int i=0; i<=NCOINS; i++)
{
position = int(float(heads[i])/NTOSSES*72);
cout<<i<<" ";
for(int j=0; j<position-1; j++)
{
cout<<" ";
}
cout<<"*"<<endl;
}
return 0;
}
int TossCoins(int numberCoins)
{
//随机抛硬币
static RandomNumber coinToss(1);
int i,tosses = 0;
for(int i=0; i<numberCoins; i++)
{
//Random(2) = 1表示正面
tosses += coinToss.Random(2);
}
return tosses;
}
第2关:用随机投点法求圆周率
任务描述
本关任务:编写一个程序,利用随机投点法计算圆周率
相关知识
设有一半径为r的圆及其外切四边形。向该正方形随机地投掷n个点。设落入圆内的点数为k。由于所投入的点在正方形上均匀分布,因而所投入的点落入圆内的概率为:

所以当n足够大时,k与n之比就逼近这一概率,从而
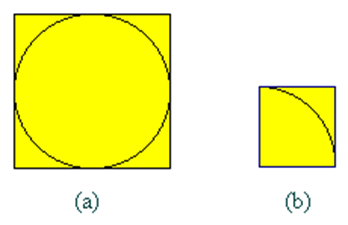
编程要求
根据提示,在右侧编辑器补充代码。
测试说明
平台会对你编写的代码进行测试:
输入:
100
输出:
n1=100 pi=3.12
开始你的任务吧,祝你成功!
参考答案:
//随机化算法 用随机投点法计算π值
#include "RandomNumber.h"
#include <iostream>
using namespace std;
double Darts(int n);
int main()
{
int n1;
cin>> n1;
cout<<"n1="<<n1<<"\npi="<<Darts(n1)<<endl;
return 0;
}
//用随机投点法计算π值
double Darts(int n)
{
static RandomNumber dart(1);
/*************begin****************/
int k=0;
for(int i=1;i<=n;i++){
double x=dart.fRandom();
double y=dart.fRandom();
if((x*x+y*y)<=1){
k++;
}
}
return 4*k/double(n);
/***************end****************/
}
第3关:解非线性方程组
任务描述
本关任务:编写程序求线性方程组。
相关知识
求解下面的非线性方程组
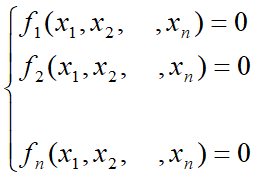
其中,x1,x2,…,xn是实变量,fi是未知量x1,x2,…,xn的非线性实函数。 要求确定上述方程组在指定求根范围内的一组解 。
解决这类问题有多种数值方法,如:牛顿法、拟牛顿法、粒子群算法等。最常用的有线性化方法和求函数极小值方法。为了求解所给的非线性方程组,构造一目标函数
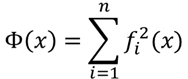
式中,x=(x1,x2,……xn)。易知,上式取得极小值点即是所求非线性方程组的一组解。
编程要求
求一个简单的二维线性方程组: x1-x2=fx1 x1+x2=fx2 根据提示,在右侧编辑器补充代码。
测试说明
平台会对你编写的代码进行测试: 例如: 输入: 1 3 输出: The original equations are: x1-x2=1 x1+x2=3 The roots are: x1=2.02104 x2=1.01445 开始你的任务吧,祝你成功!
参考代码:
//随机化算法 解线性方程组
#include "RandomNumber.h"
#include <iostream>
using namespace std;
bool NonLinear(double *x0,double *dx0,double *x,double *fx,double a0,
double epsilon,double k,int n,int Steps,int M);
double f(double *x,double *fx);
int main()
{
double *x0, //根初值
*x, //根
*dx0, //增量初值
*fx, // 函数值
a0 = 0.0001, //步长
epsilon = 0.01, //精度
k = 1.1; //步长变参
int n = 2, //方程个数
Steps = 10000, //执行次数
M = 1000; //失败次数
x0 = new double[n+1];
dx0 = new double[n+1];
x = new double[n+1];
fx = new double[n+1];
cin >> fx[1];
cin >> fx[2];
//根初值
x0[1] = 0.0;
x0[2] = 0.0;
//增量初值
dx0[1] = 0.01;
dx0[2] = 0.01;
cout<<"The original equations are:"<<endl;
cout<<"x1-x2="<<fx[1]<<endl;
cout<<"x1+x2="<<fx[2]<<endl;
cout<<"The roots are:"<<endl;
bool flag = NonLinear(x0,dx0,x,fx,a0,epsilon,k,n,Steps,M);
while(!flag)
{
flag = NonLinear(x0,dx0,x,fx,a0,epsilon,k,n,Steps,M);
}
for(int i=1; i<=n; i++)
{
cout<<"x"<<i<<"="<<x[i]<<" ";
}
cout<<endl;
return 0;
}
//解非线性方程组的随机化算法
bool NonLinear(double *x0,double *dx0,double *x,double *fx,double a0,
double epsilon,double k,int n,int Steps,int M)
{
static RandomNumber rnd(1);
bool success; //搜索成功标志
double *dx,*r;
dx = new double[n+1]; //步进增量向量
r = new double[n+1]; //搜索方向向量
int mm = 0; //当前搜索失败次数
int j = 0; //迭代次数
double a = a0; //步长因子
for(int i=1; i<=n; i++)
{
x[i] = x0[i];
dx[i] = dx0[i];
}
double fy = f(x,fx); //计算目标函数值
double min = fy; //当前最优值
while(j<Steps)
{
//(1)计算随机搜索步长
/***********begin**************/
if(fy<min){
min=fy;
a*=k;
success=true;
}
else{
mm++;
if(mm>M){
a/=k;
}
success=false;
}
if(min<epsilon){
break;
}
/************end***************/
//(2)计算随机搜索方向和增量
/***********begin**************/
for(int i=1;i<=n;i++){
r[i]=2.0*rnd.fRandom()-1;
}
if(success){
for(int i=1;i<=n;i++){
dx[i]=a*r[i];
}
}
else {
for(int i=1;i<=n;i++){
dx[i]=a*r[i]-dx[i];
}
}
/************end***************/
//(3)计算随机搜索点
/***********begin**************/
for(int i=1;i<=n;i++){
x[i]+=dx[i];
}
/************end***************/
//(4)计算目标函数值
/***********begin**************/
fy=f(x,fx);
j++;
/************end***************/
}
if(fy<=epsilon)
{
return true;
}
else
{
return false;
}
}
double f(double *x, double* fx)
{
/***********begin**************/
return (x[1]-x[2]-fx[1])*(x[1]-x[2]-fx[1])
+(x[1]+x[2]-fx[2])*(x[1]+x[2]-fx[2]);
/************end***************/
}
如果对你有所帮助,感谢点赞加收藏!
关于接下来的实验内容,我也会在【WRITE-BUG数字空间】更新,也可以为大家带来更好的观感,带来更多的分享,欢迎大家前来浏览。
算法设计与分析:随机化算法(作业-必做)(头歌实验) -文章频道 - 我的学习圈 - 个人学习圈 (writebug.com)![]() https://www.writebug.com/article/8c2ca050-f3e6-11ed-a099-0242ac14000d
https://www.writebug.com/article/8c2ca050-f3e6-11ed-a099-0242ac14000d