引言
北京时间:2023/5/17/22:19,不知道是以前学的不够扎实,还是很久没有学习相关知识,对有的知识可以说是遗忘了许多,以该篇博客有关知识为例,我发现我对迭代器和模板的有关知识的理解还不够透彻,不知道是对以前知识的遗忘,还是现在所学确实有难度,反正导致我很懵,希望当该篇博客写完,能让我的理解更上一层楼吧!并且今天是周三,没课,但是有些摆烂,因素很多,可能是前几天学习强度有一些大导致的,也可能是自我要求变高了,也可能是整个宿舍都去图书馆,独独我没去而感到一定的压力,当然也可能是最近的课程难度上升,不容易学进去,从而导致容易摆烂,反正各个因素都有,在此值得思索,该篇博客是一个过度,因为只要把该篇博客写完,我们就可以进入新知识的学习,有关哈希表的知识,所以让我们在该篇博客把有关set和map的知识收尾,利用之前所学的红黑树知识,自我封装map和set,当然只是简易封装,前提是需要把迭代器和模板有关的知识复习一下,因为这两个STL里的地头蛇、老油条咱们玩不过它们呀!呜呜呜!

STL中有关map和set的知识
什么是map和set
首先明白set和map就是我们之前学习过的搜索树,并且由于它们的底层使用的是红黑树进行封装,所以它们本质上就是一棵平衡搜索二叉树 ,并且我们知道搜索树可以分为Key模型和Key/Value模型,所以此时的set就是一棵Key模型的平衡搜索二叉树,map就是一棵Key/Value模型的平衡搜索二叉树,并且最终可以称它们为非序列式容器,或者关联式容器
什么是序列式容器,什么是关联式容器
这个问题想必很好回答,序列式容器从名称上不难理解,就是我们之前学习的像list、vector、deque、stack……,这一类线性结构的容器,并且明白,这一类线性结构容器本质上是用来存储数据,除了存储数据并没有其它方面的特点,而关联式容器(树状结构),就是像上述所说的有关set和map这样的平衡搜索二叉树,虽然set和map也是用来存储数据的,但是与序列式容器不同的是,其里面存储的是<key,value>结构的键值对,所以又由于它树状结构的优势,此时set和map在数据检索时的效率远高于序列式容器,所以set和map被广泛运用于现实生活中各种与搜索相关的场景
什么是键值对
从上述语句描述中,我们可以看出,键值对就是一个<key,value>的结构体而已,在STL中也存在着该容器,头文件map,表明你可以直接通过map头文件直接调用该容器,有关结构定义如下图所示:

注意: 如上述所说键值对就是一个pair结构体,并且我们可以直接使用默认构造函数去构造一个对应模板参数类型的数据类型,所以一般使用方法就是 pair<T1,T2>(x,y); ,但是map中,为了可以更加方便的使用,就封装了一个 make_pair() 供我们使用,如上述一般,可以看出,不过也就是一个简单的二次封装而已,明白了pair结构体的构建,此时还要知道,对于pair这个键值对来说,其中的first代表的就是key值,也就是键,而second代表的就是value数据,也就是值,所以pair结构体中的两个数据,第一个表示的就是键,第二个表示的就是值,所以称为键值对
set和map具体使用方法
set的使用方法 :set使用官方文档
从文档中,我们可以看出set的使用方法大体上和我们之前学习的有关容器是一致的,以插入、删除、查找为主体,配以迭代器、反向迭代器、运算符重载、计数、大小、交换相关接口为辅,所以使用起来对于我们来说还是较为简单的,如下图所示:
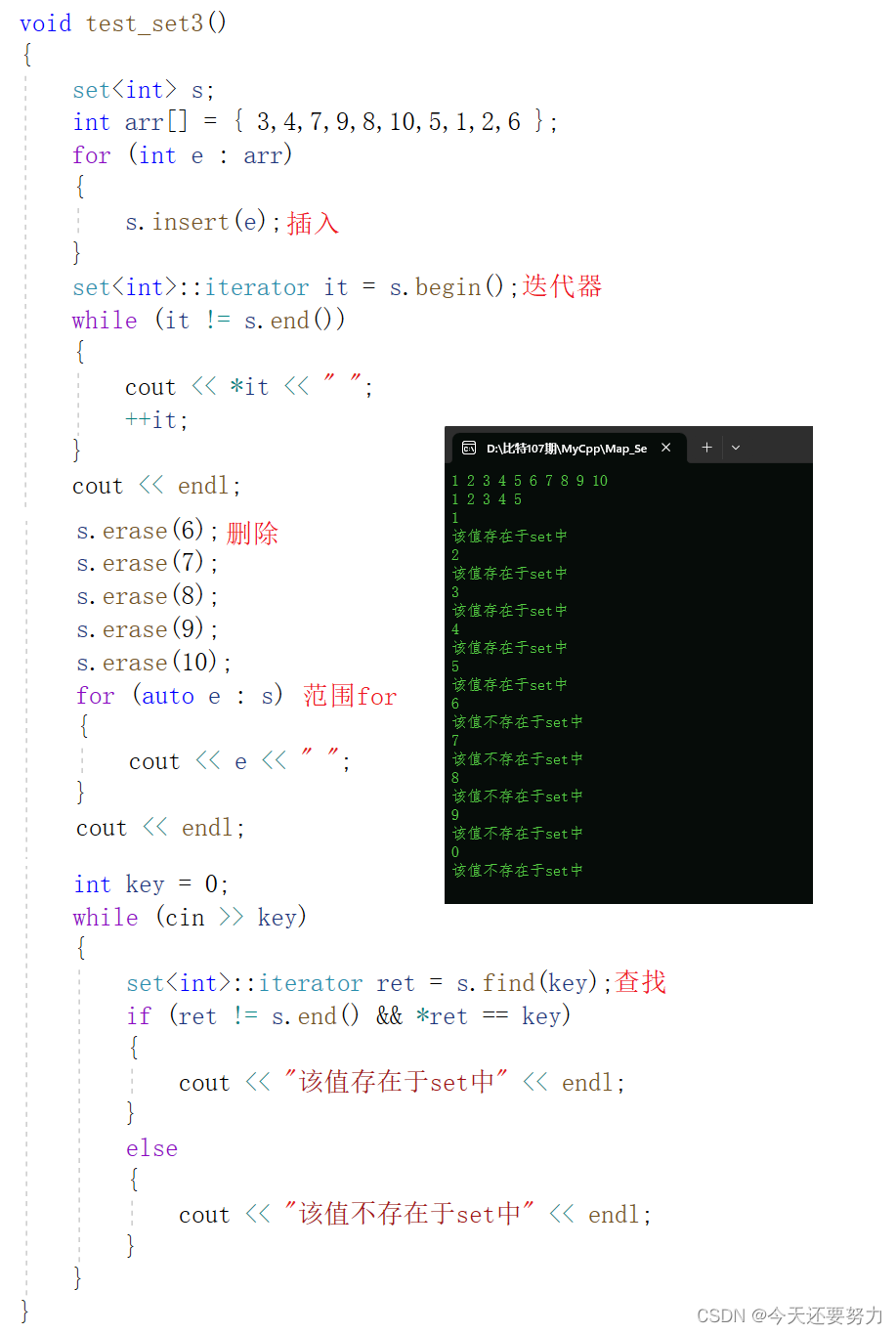
什么是multiset
但是我们明白,由于set是一棵平衡搜索二叉树,所以此时它是不允许插入重复数据的,所以导致重复数据插入不成功,所以STL库中为了解决这个问题,它为我们提供了一个除无法插入相同数据之外和set相同的库 multiset ,使用方法这里不过多强调,和set如出一撤,就只是可以插入两个相同的数据而已,别无其它区别,接下来让我们去看看map的具体使用吧!
map的使用方法:map使用官方文档
map同理由于是一棵平衡搜索二叉树,所以使用方法类似,和set唯一的区别就是,set中存储的数据是一个唯一的key值,而map中存储的数据是一个键值对,也就是pair结构体,map通过存储的该结构体,此时就可以直接通过key值查找到对应的一些列value数据,这也就是K/V模型的好处和优势,具体使用方法如下:

如上述代码所示,就是map中主要接口的大致使用,虽然还有一些计数和计算大小等接口,但是这些接口跟我们使用map并没有什么太大的关系,但是,在map中存在一个非常实用的东西,就是方括号这个运算符的重载,这个方括号的重载在map中算是非常重要的一个接口,所以此时我们就来看看为什么方括号在map中很重要吧,代码如下:
没有使用方括号运算符([]),统计水果出现的次数代码:
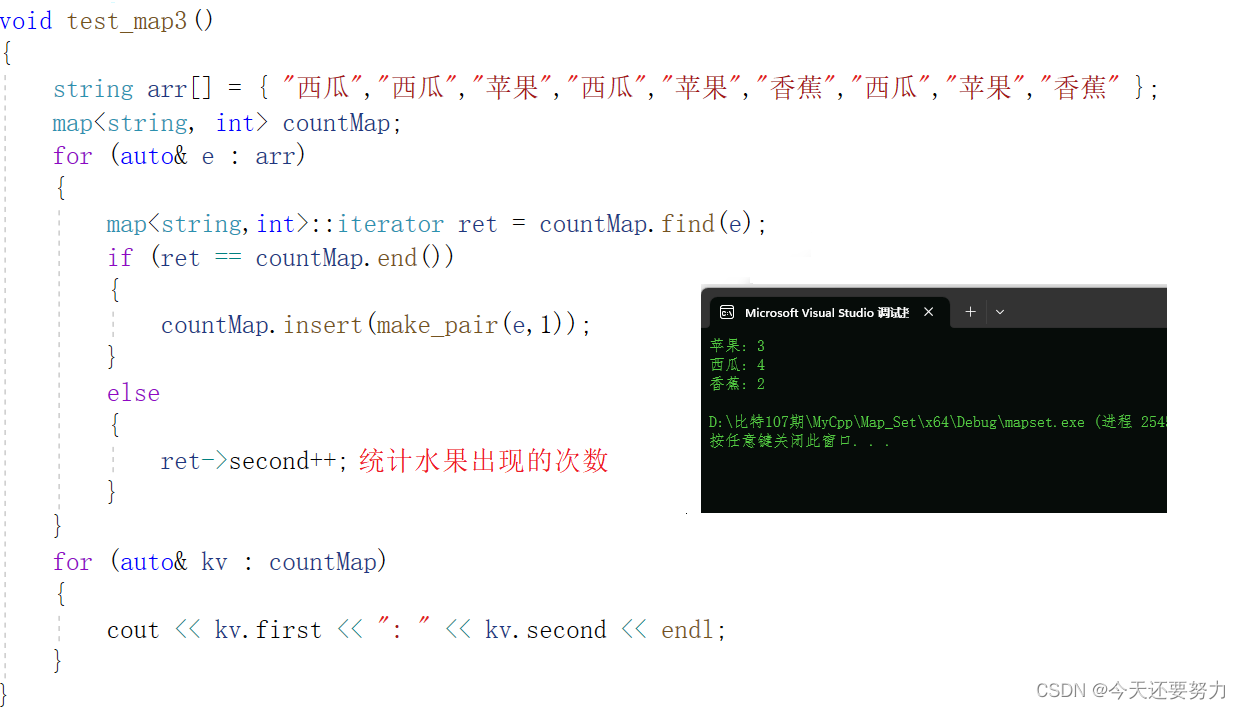
当使用了方括号([])来统计水果出现的次数:

简单对比可以发现,在得到的效果相同的情况下,使用了方括号之后,代码量大大减少,根本不需要使用find接口和insert接口,甚至连迭代器都不需要使用,我们就可以达到相同的效果,就冲着这一点出发,就已经可以看出map中方括号运算符的重载有多牛了,但是逆向思考,也可以看出方括号的原理是有一定难度的,虽然知道实现起来,本质还是去封装插入、查找、迭代器等接口,所以接下来就让我们来详细的分析一下有关方括号的知识,如下:
详解map中方括号的使用
在map中,我们可以寻找到对应方括号的代码实现如下:

第一眼看过去,这句代码是非常的抽象的,但是莫得慌张,让我们一步一步的来解析它就行了,如下:
1.首先明白,上述代码中的 insert 的有关知识,我们可以发现,如该代码一样:
pair<iterator,bool> insert(const value_type& val); 此时insert接口的返回值是一个pair结构体(键值对),并且此时插入的是一个value_type类型的val常量,如果插入成功就返回pair结构体中的迭代器和相应的bool值(true),如果插入失败同样会返回pair结构体中的迭代器,但此时的bool值是false,所以此时明白了有关insert接口的知识,此时我们就可以正式的去解析上述代码了
2.this->insert(make_pair(k, mapped_type())) 语句,同理上述有关insert的知识,只不过此时插入的不是一个val常量,而是一个pair结构体,所以具体表示的就是:向 map 容器插入一个新的pair结构体(键值对),其中 k 表示要插入的键,mapped_type() 表示要插入的值(通过不同模板参数类型的默认构造函数初始化),同理返回值是 pair<iterator,bool> ,插入成功返回对应pair结构体(键值对)的迭代器和bool值(true),插入失败同样返回对应pair结构体(键值对)的迭代器和bool值(false)
3.this->insert(make_pair(k, mapped_type())).first 表示使用insert的返回值,也就是对应pair结构体(键值对)的迭代器去访问该pair结构体的第一个元素,也就是key,键
4.*((this->insert(make_pair(k, mapped_type()))).first) 同理,只不过此时多了一个解引用( * )符号,表示的是,对pair结构体(键值对)的迭代器进行解引用,因为迭代器本质就是一个指针类型,然后获取到该迭代器指向的地址,也就是pair结构体的地址,然后访问该pair结构体中的第一个元素key
5.(*((this->insert(make_pair(k, mapped_type()))).first)).second 同理第四点,,只不过最后直接通过该key键访问到指定对应的键值对对象(值)
明白了上述知识之后,此时就有了一定的改进写法,如下:

所以此时由于上述方括号的一系列知识,此时方括号就同时具有多种功能,1.插入 2.修改 3.插入+修改 4.查找
如下图所示:

multimap
同理multiset,为了支持插入重复数据,STL也为我们提供了multimap这个容器,使用方法上同理map,这里不多做讲解,接下来让我们进入该篇博客的主题,也就是使用红黑树进行set和map的底层封装
set和map的自我简易封装
搞定了上述有关set和map在基本使用上的问题,此时我们就正式进入set和map的简易封装,首先明白一点,和上述所说的一样,set和map都是通过封装红黑树来实现自我封装的,这也是为什么set和map属于平衡搜索二叉树,注意: 由于set是key模型,所以底层在调用红黑树进行封装的时候,一定要考虑该红黑树的参数和比较大小方面是否符合对应set的传参和比较大小,同理由于map是key/value模型,底层调用红黑树时,也一定要考虑传参和比较大小等问题, 明白了这点,我们就可以知道,由于set和map具体模型不同,导致它们的传参肯定不同,一个只要传一个单独的key值,而另一个却要传两个值,key和value,所以导致如果它们使用同一棵红黑树的话,此时就一定会出现问题,所以最简单的解决方法就是实现两个不同的红黑树,一棵提供给set使用,一棵提供给map使用,但是在STL中,大佬写代码肯定是不会这么简单的,所以此时就让我们去STL中看看红黑树是如何实现,从而导致可以让一棵红黑树同时供给给set和map同时使用,源码如下:
首先是set和map源码中调用红黑树时进行的传参,如下代码所示:
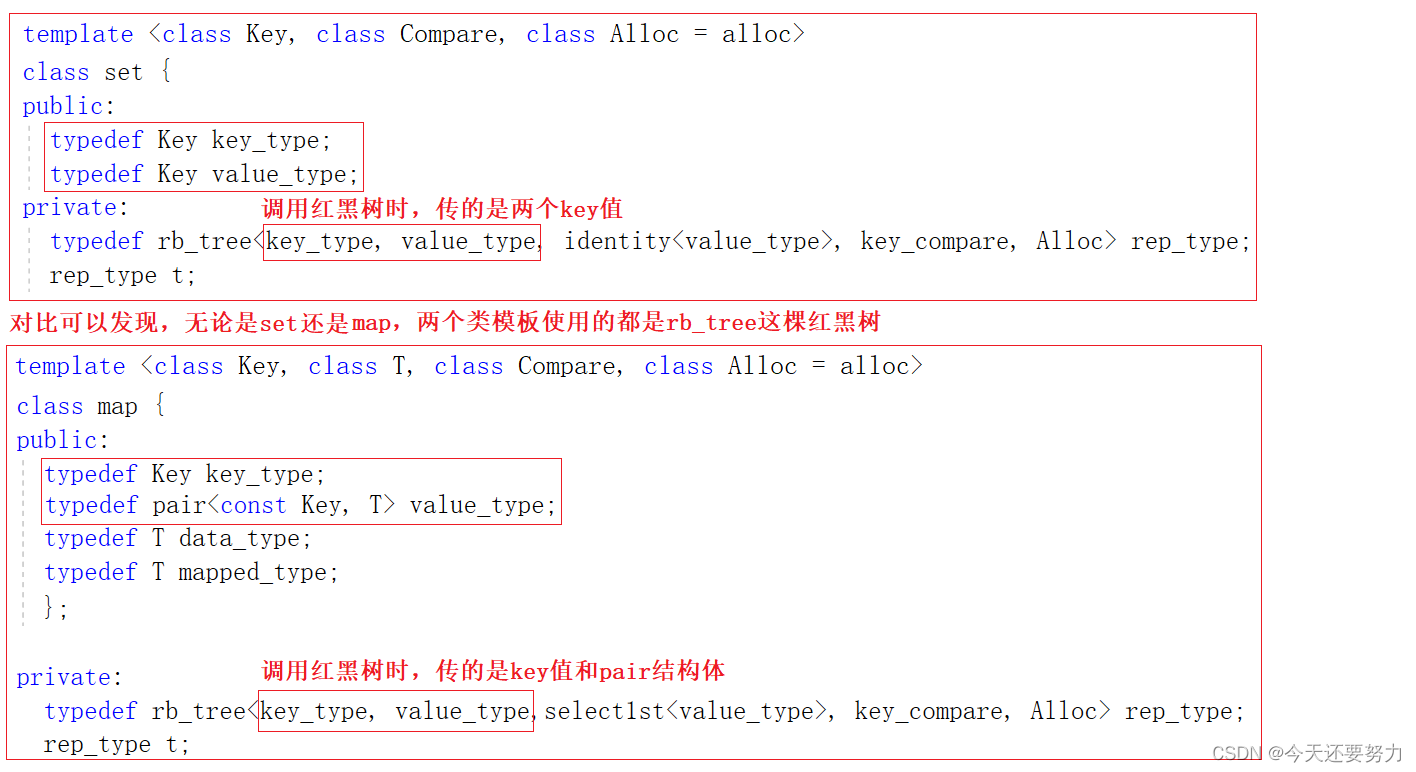
可以发现,此时STL中并没有同时实现两棵红黑树,而是使用同一棵红黑树,只不过此时set和map进行的传参不同,所以此时想要明白源码是如何通过一棵红黑树实现两个不同的模型,就需要去看看红黑树具体是如何接收参数和使用参数,如下代码:
set调用红黑树参数的传递过程:
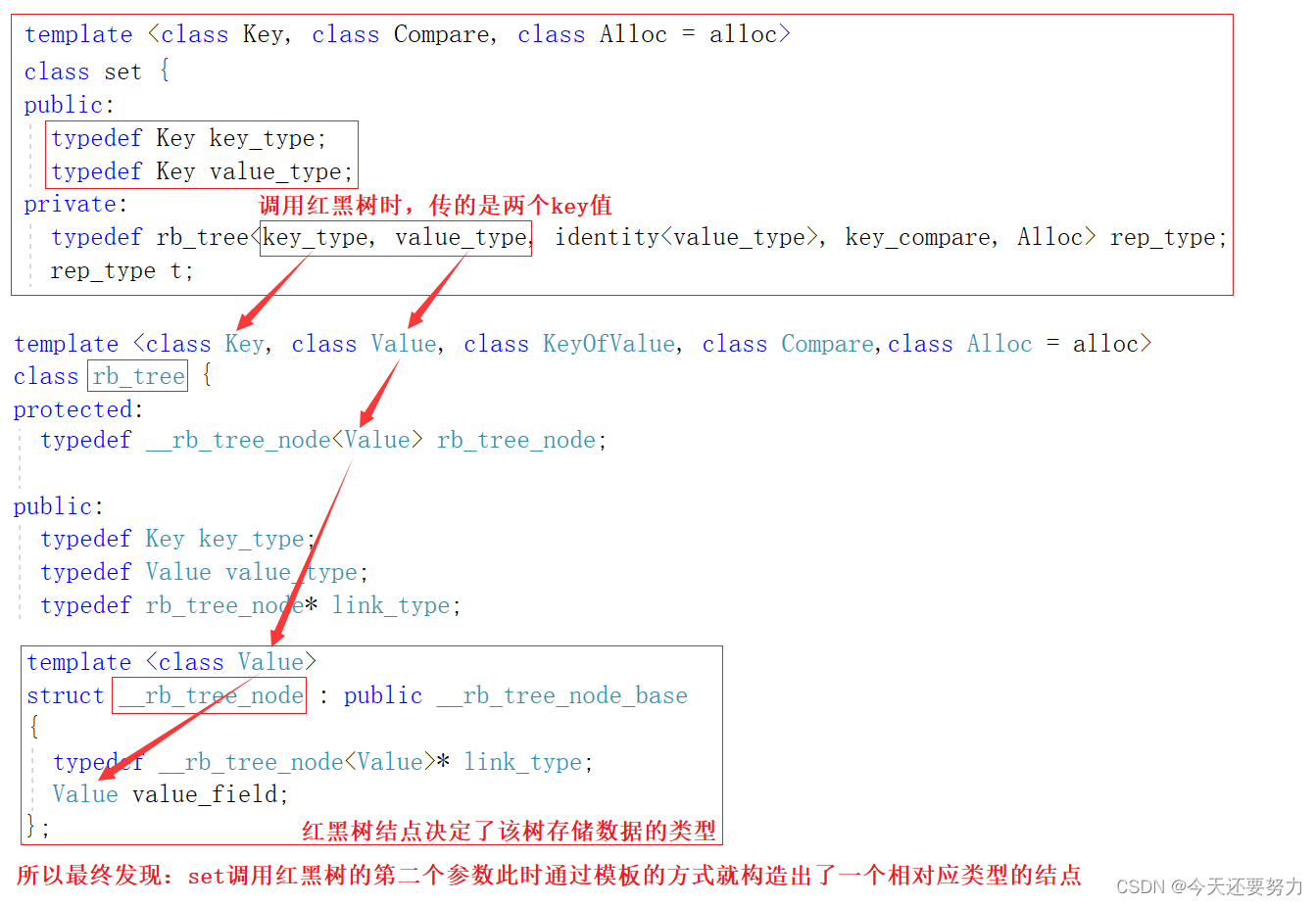
同理,map调用红黑树,参数传递过程:
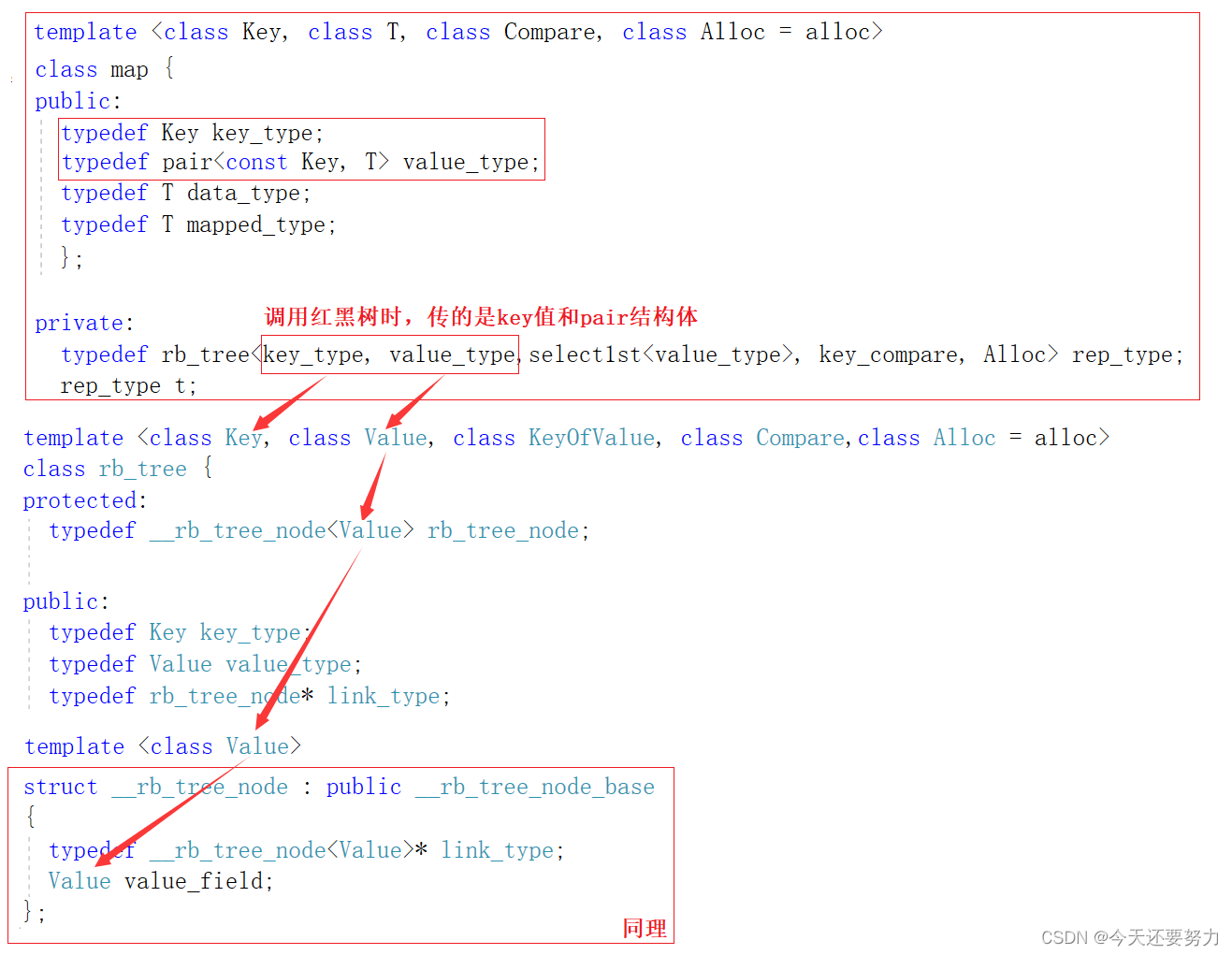
同理,最终发现,map也是通过第二个参数 value_type(pair<const Key,T>) 最终通过模板参数的形式构造出了一个相对应类型的红黑树结点
所以此时本质上参数传递就是 set<K> -> rb_tree<K,K> 和 map<K,V> -> rb_tree<K,pair<const K,V>> 然后通过第二个模板参数进行红黑树结点的构造,达到构造不同类型结点的效果,所以在STL源码中,map和set的实现不是实现两份不同的红黑树代码来封装,而是通过泛型编程的原理,通过模板的形式来控制不同的数据类型
注意: 如上述所说,第二个模板参数是用来决定该红黑树结点的数据类型,那么第一个参数是用来干什么的呢?所以此时我们就不能光看到数据类型的控制,我们还要考虑到接口的调用,类似于删除、查找,它们本质并不需要使用pair结构体参数,因为只要通过key键就能找到对应的数据值,所以像删除和查找这一类的接口,本质都是直接使用key值就行了,所以第一个参数就是为了提供给这些只需要使用key值作为参数的接口使用,所以本质,上述红黑树的这种通过模板控制类型的方法,是为了可以更好的提供给map使用,让map不仅可以构造出 pair<const K,V> 类型的数据,也可以通过Key值找到对应的Value,然后删除或者替换对应的Value值,本质和set没有太大的关系(冗余一个参数)
正式进入set和map的封装
明白了上述知识之后,此时就可以正式进入set和map的封装了,我们使用的方法和STL中的源码是类似的,也是使用泛型的方式,用模板来搞定不同的数据类型,但是在使用模板解决类型不匹配问题的时候,我们会发现,除了像insert接口中参数类型不匹配需要使用模板参数之外,在insert接口内部,也存在一定的问题,这个问题就是当我们在比较大小的时候,set由于是直接使用key值作为参数,所以直接使用的就是key作为比较大小的数据,但是像pair结构体(键值对),其中就存在两个数据,我们并不能很好的控制它,让它以其中的键去进行大小的比较(pair结构体中的first数据),虽然由于pair结构是一个类,存在自己比较大小的方法,但是该方法并不是使用该结构体中的first数据(键)去进行比较,所以也不符合我们的期望,所以此时我们就要对代码进行改进,以保证代码在比较大小方面逻辑性的正确,因为数据值大小的比较在搜索二叉树中十分重要
问题详述:
虽然之前我们可以直接通过去取data的first(因为data是一个pair类型的数据)来进行比较大小,但是此时由于我们使用的是泛型编程,导致参数是一个模板参数,具体是什么类型我们并不知道,只有被其它类调用,进行了传参之后才知道,所以我们并不能确定此时的这个模板参数的类型是pair结构体还是单独一个Key值,如果是单独一个Key值,那么此时data数据就不可能拥有什么first数据,什么second数据,导致代码出现问题,所以此时我们就需要像如下代码一样,进行改进:

如上图,通过在对应set和map中构建一个内部类的方式,再把该类作为一个模板参数传递到对应调用的红黑树,让该红黑树可以根据该内部类调用到该类中对应的仿函数,根据仿函数的实现(返回对应数据),最终获取到我们想要的,可以直接进行大小比较的数据值(本质还是因为map的实现,使用的红黑树需要是pair结构体类型),所以此时在insert接口中,我们就可以使用上图中对应的内部类的模板参数,然后创建一个类对象来调用到对应类中的仿函数啦!具体如下图所示:
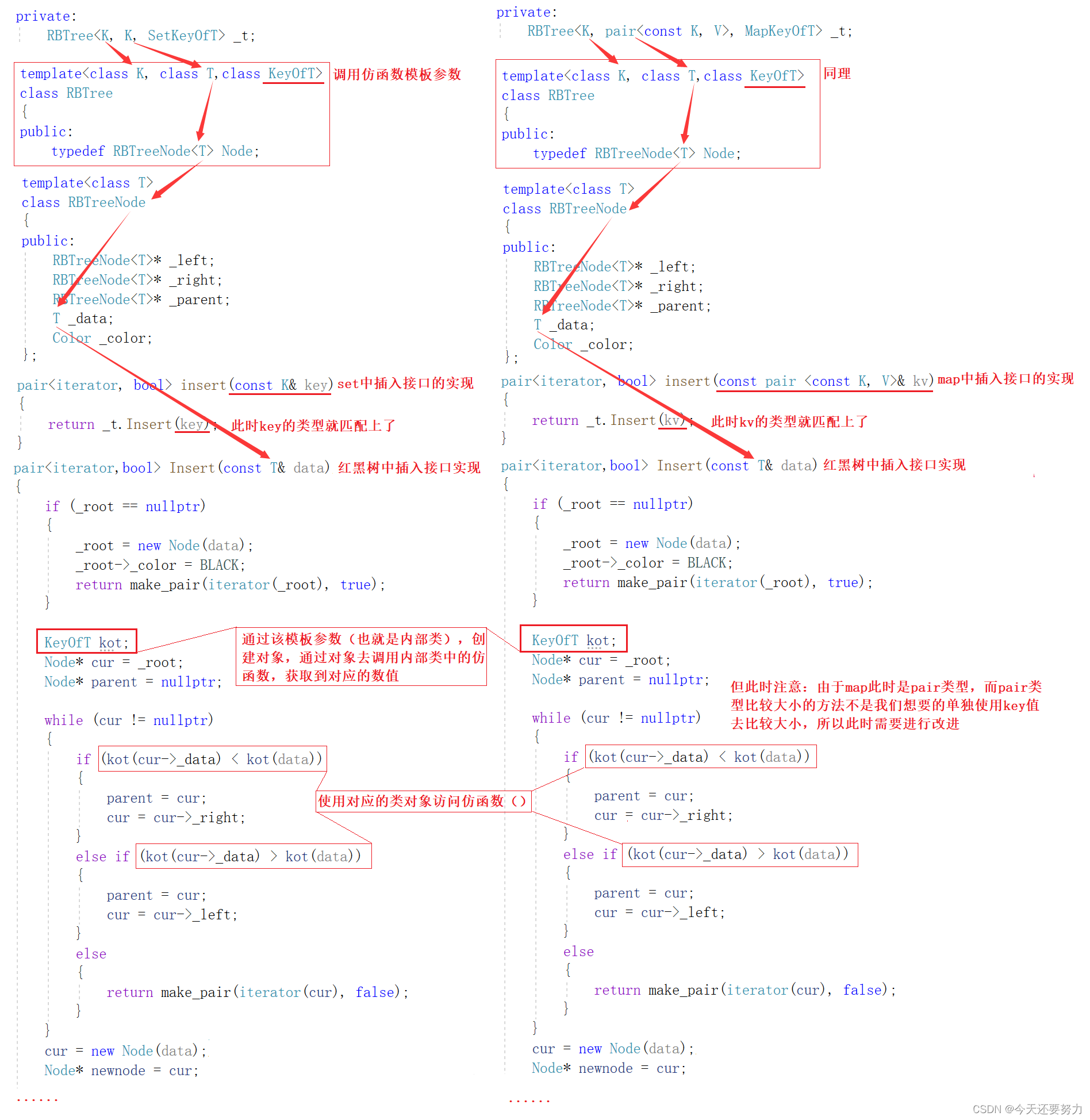
总:本质上述搞了这么多,就是为了可以让map可以和set一起吃饭而已,同一份代码被不同数据类型的类调用,当然这也就是泛型编程强大的地方之一
set和map中迭代器的封装
搞定了上述知识,此时对红黑树中插入接口和以前不同的一些奇奇怪怪的实现,可以说是了解的差不多的,所以对于set和map中插入、查找、删除这些接口我们就不多做过多了解,因为明白了上述的插入接口有关知识,查找和删除同理,此时我们就来看看STL中的另一个天王(迭代器),具体如何封装实现,并且明白,每一个容器都有着自己独特的迭代器实现,本质上是为了在使用迭代器时,可以以一种统一的方式进行使用,所以迭代器这个概念本质就是为了可以让不同的容器实现出统一的使用方式 ,并且如下述所示,一般的容器都具有对应功能:
| 迭代器常见接口 |
|---|
*it:返回迭代器 it 所指向的当前元素 |
it->member:等价于 (*it).member,返回迭代器 it 所指向的对象的成员 member |
it++ 或 ++it:在使用迭代器遍历容器时,经常需要将迭代器前移或后移一个位置,这时可以使用前缀或后缀自增运算符 (++),使迭代器指向其他元素 |
it-- 或 --it:和运算符 ++ 类似,这里使用了运算符 --,使迭代器指向前一个元素 |
| != 或 ==:比较两个迭代器是否相同或不同,返回比较结果的布尔值(true 或 false) |
begin() 和 end():分别返回指向容器第一个元素和最后一个元素之后一个位置的迭代器 |
cbegin() 和 cend():分别返回指向容器第一个元素和最后一个元素之后一个位置的 const 迭代器 |
rbegin() 和 rend():reverse(反向)版本的 begin() 和 end() 函数,返回指向容器最后一个元素和第一个元素之前一个位置的迭代器 |
crbegin() 和 crend():分别返回指向容器最后一个元素和第一个元素之前一个位置的 const 反向迭代器 |
正式进入迭代器的封装
明白了上述知识,此时就让我们一起来看看set和map中迭代器的实现吧!(本质还是对红黑树中的迭代器就行封装)
多的不说,自我封装的开始都是去看一看源码中的封装,源码如下:
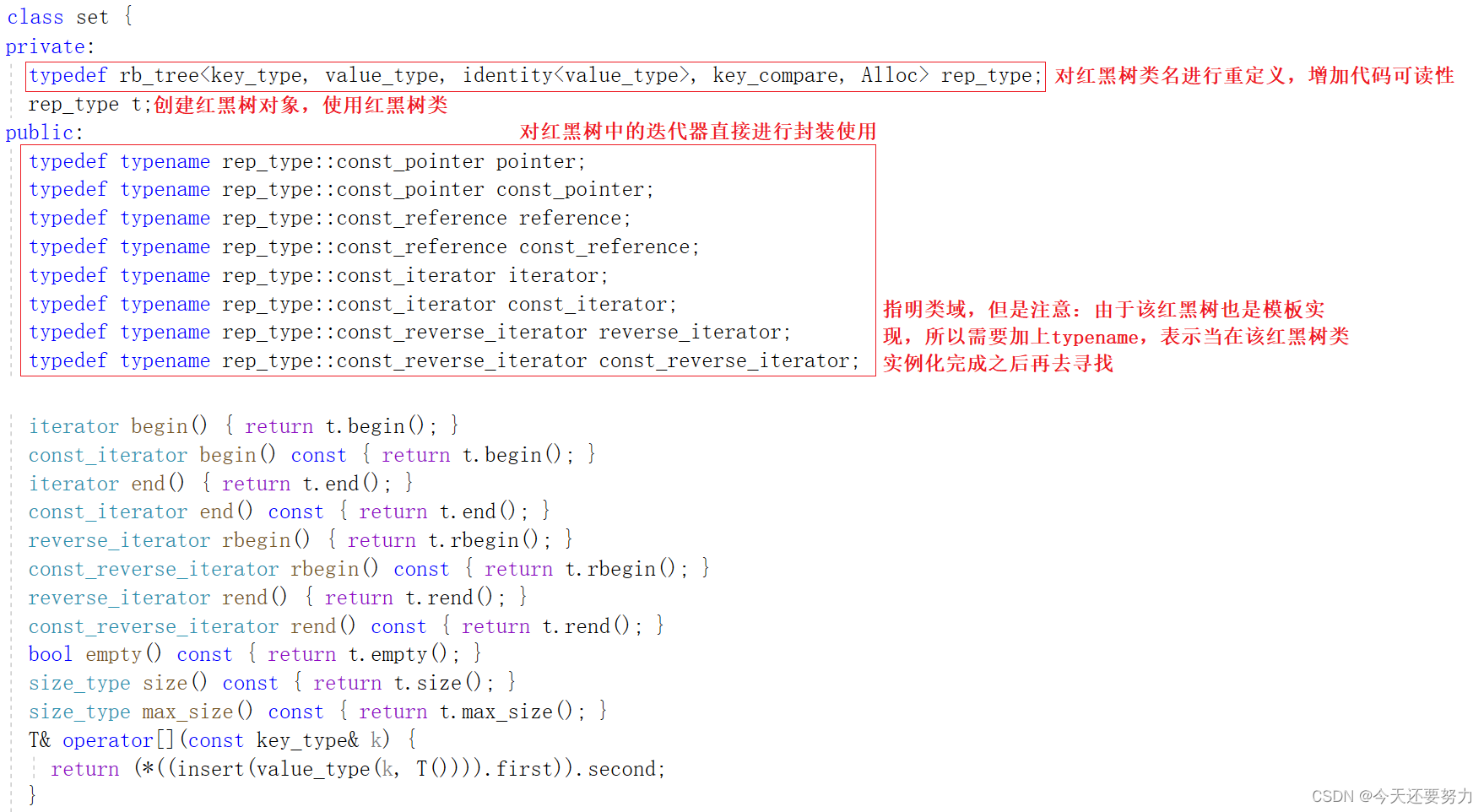
map同理,这里不多做展示
所以明白,想要自己实现set和map中有关迭代器的知识,只要去封装红黑树中的迭代器就行,本质就是去自我实现红黑树中有关迭代器的知识,所以同理,当我们想要自己实现红黑树中的迭代器时,我们就得先去看一下STL中源码如何实现,So,here we go!
红黑树迭代器源码如下:

所以如上图所示,当我们像源码一样,将自我实现的红黑树中的迭代器编写完成,此时set和map就可以利用该红黑树的类型名创建出相应的对象,通过该对象来调用红黑树中迭代器的实现代码,自我简易实现红黑树迭代器代码:

注意: 此时上述代码在寻找红黑树的下一个结点和上一个结点中,我们使用的寻找方法是针对于于一棵正常实现的红黑树而言,而STL库中的遍历方法与我们不同,因为它对于红黑树的整体结构进行了一定的改进,如下图所示:
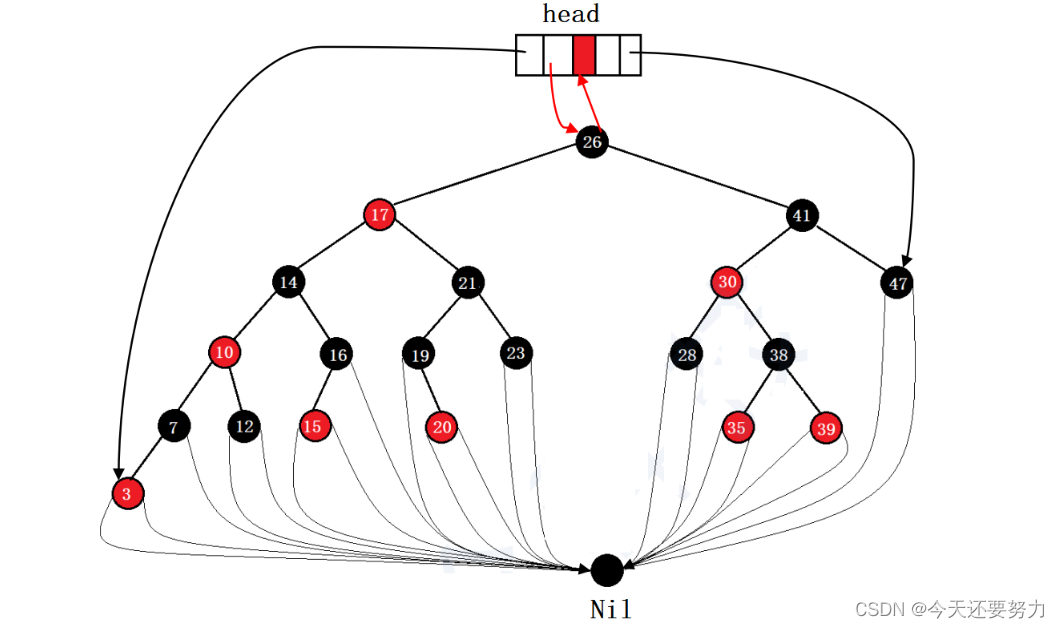
所以由于红黑树的结构图不同,在代码实现上也不同,但是原理大相径庭
搞定了上述知识,红黑树中有关迭代器的知识大部分我们就搞定了,但是此时还有一定的细节需要我们处理,当然这些细节也就是set和map导致,例如:在set中由于只有一个Key,所以在构建搜索树的时候,这个Key值就不允许被修改,因为如果该值运行被修改,那么就会导致整棵搜索二叉树失去效果,所以当我们在实现set的时候,无论是普通迭代器还是const迭代器,我们使用的都是红黑树中的const迭代器,并且在map中同理,我们要控制pair结构体(键值对)的第一个数据不允许被修改,第二个数据允许被修改,具体情况,如下:
*it 允许被修改,如果被修改会导致该树不是搜索树,所以key值一定不允许被修改,源码中的解决方案:无论是普通迭代器还是const迭代器我们都使用const迭代器,如下图所示:

但是,当我们将set和map中的普通迭代器和const迭代器都定义成调用红黑树中的const迭代器时,此时就会出现编译错误,显示的是无法将普通迭代器转换为const迭代器,这是什么原因呢?
如下图:

所以解决方法就是再去实现一个可以让普通迭代器转化为const迭代器的构造函数,这样,无论是普通迭代器,还是const迭代器,都可以完成相应的转化,并且,如果iterator是一个真普通迭代器,那么此时该构造函数就是一个拷贝构造函数,如果此时的iterator是一个假普通迭代器(类似于set中这种),那么此时就让这个假普通迭代器去构造成一个const_iterator就行了,具体如下图所示:

set和map封装
set封装代码如下:
#include"rb_tree.h"
namespace wwx
{
template<class K>
class set
{
public:
class SetKeyOfT
{
public:
const K& operator()(const K& key)
{
return key;
}
};
typedef typename RBTree<K, K, SetKeyOfT>::const_iterator iterator;
typedef typename RBTree<K, K, SetKeyOfT>::const_iterator const_iterator;
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
pair<iterator, bool> insert(const K& key)
{
return _t.Insert(key);
}
private:
RBTree<K, K, SetKeyOfT> _t;
};
map封装代码如下:
#include"rb_tree.h"
namespace wwx1
{
template<class K, class V>
class map
{
public:
class MapKeyOfT
{
public:
const K& operator()(const pair<const K,V>& kv)
{
return kv.first;
}
};
typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator;
typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::const_iterator const_iterator;
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
pair<iterator, bool> insert(const pair <const K, V>& kv)
{
return _t.Insert(kv);
}
V& operator[](const K& key)
{
pair<iterator,bool> ret = _t.Insert(make_pair(key, V()));
return ret.first->second;
}
private:
RBTree<K, pair<const K, V>, MapKeyOfT> _t;
};
红黑树完整代码如下:
#pragma once
#include<iostream>
#include<map>
#include<iostream>
#include<string>
#include<vector>
#include<set>
#include<cassert>
#include<time.h>
using namespace std;
enum Color
{
RED,
BLACK
};
//此时按照库里面的代码实现方法,所以此时我们需要把这棵红黑树进行一定的改变(重点也就是模板参数的改变,从两个模板参数变成一个)
//从而让这棵红黑树满足泛型的要求,可以达到传不同的模板参数就能实现不同的类型(具体指的是:key模型、key/value模型)
//但是注意:此时因为map中调用红黑树时,传的是pair结构体,并且pair结构体比较大小的方式和我们实现的比较方式是有区别的,所以需要改进
template<class T>
class RBTreeNode
{
public:
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
RBTreeNode<T>* _parent;
T _data;
Color _color;
RBTreeNode(const T& data)
:_left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _color(RED)
{}
};
//搞定了模板参数比较大小的问题,此时进入迭代器有关问题
template<class T, class Ref, class Ptr>//此时Ref/Ptr这两个模板参数可以说是异常的熟悉,不服就去复习list(目的:就是为了实现const类型的迭代器和普通类型的迭代器)
struct __RBTreeIterator
{
typedef RBTreeNode<T> Node;
typedef __RBTreeIterator<T, Ref, Ptr> iterator;
Node* _node;
__RBTreeIterator(Node* node)//用一个node来构造该迭代器(如下述使用cur结点,iterator(cur))
:_node(node)
{}
//此时由于set的普通迭代器和const迭代器都是const迭代器,所以当set在使用 iterator begin(){ return _t.begin()};
//时,就会因为_t.begin()接口是红黑树中的接口,所以是一个普通迭代器,但是返回值iterator却是一个const迭代器
//所以我们需要有一个普通迭代器转换为const迭代器的构造函数(不好理解)
//但是此时想要实现这个构造函数,此时有一个坑,因为我们使用的是模板,所以并不知道对应迭代器是什么类型,所以需要把模板参数给到
__RBTreeIterator(const __RBTreeIterator<T, T&, T*>& it)
:_node(it._node)//注意:const迭代器可以隐式类型转换成普通迭代器
{}
//1.typedef __RBTreeIterator<T, T&, T*> iterator;如果传到上述拷贝构造函数的是这个类型,那么此时就是拷贝构造函数
//2.typedef __RBTreeIterator<T, const T&, const T*> const_iterator;如果是这个类型,那么此时就是构造函数(本质就是自己构造成自己 )
Ref operator*()//解引用返回的自然而然就是对应的数据
{
return _node->_data;
}
Ptr operator->()//这个位置有待复习
{
return &_node->_data;
}
bool operator==(const iterator& it)
{
return _node == it._node;
}
bool operator!=(const iterator& it)
{
return _node != it._node;
}
iterator& operator++()
{//红黑树的加加,就是按照中序走走而已(但,注意:此时的++的前提是,已经处于begin位置了,所以根本不需要找begin位置)
if (_node->_right != nullptr)
{//1.此时表示的就是当右子树存在的时候,我们就去找右子树的最左结点(注意:是在最左结点的前提下)
Node* subLeft = _node->_right;
while (subLeft->_left != nullptr) // 13
{ // 8 17
subLeft = subLeft->_left; // 1 11 15 25
} // 6 22 27
_node = subLeft;
}
else
{//2.右为空,我们就沿着根的路径,找孩子是父亲左的那个祖先(也就是当++了一步,从1来到6的时候,此时6的右为空,我们就需要返回到8)
//此时的8也就是6的祖先,也就是祖先的左孩子是6的父亲的那个结点
Node* cur = _node;
Node* parent = cur->_parent;
while (parent != nullptr && parent->_right == cur)//这步一定要先判断一个parent不等于nullptr,不然如果为空,就会导致很坑,因为使用了空指针去访问parent指针
{
cur = parent;
parent = parent->_parent;//这步就是为了找到8,并且为了防止死循环,所以上述条件一定需要指明cur在那个结点的右
}
//代码走到这里,就说明,找到祖先结点,也就是下一个结点,此时迭代就行
_node = parent;
}
return *this;//this表示Node结点指针的地址,而*this表示的就是this指针指向的地址
}
iterator operator--()
{//减减同理加加,中序左根右,减减就变成右根左
if (_node->_left != nullptr)
{
//1.左不为空,找左子树的最右孩子
Node* subRight = _node-> _left;
while (subRight->_right != nullptr)
{
subRight = subRight->_right;
}
_node = subRight;
}
else//2.明白条件,也就是左为空的情况下
{
Node* cur = _node;
Node* parent = cur->_parent;
while (parent != nullptr && parent->_left == cur) // 13
{//上面这个循环不要困惑,如果在左边的话,不进循环之间找父结点进行 // 8 17
cur = parent; // 1 11 15 25
parent = parent->_parent; // 6 22 27
}
_node = parent;
}
}
};
//此时由于map和set中比较大小的方式不同,所以红黑树中的比较方式需要改变,最好的方法就是使用仿函数
//也就是让key去比较大小,而不是直接用pair去比较大小,所以此时也就是把pair中的key取出来,使用pair中的key去进行比较
template<class K, class T,class KeyOfT>//此时红黑树本身是不知道T是什么的,只有调用这棵红黑树的类知道,所以此时需要改进
class RBTree //例:map知道它是pair结构体,而set知道它是Key(所以此时就使用这个参数作为一个返回值去使用)
{ //并且明白:这个位置写博客的时候要去画一个图
public:
typedef RBTreeNode<T> Node;
typedef __RBTreeIterator<T, T&, T*> iterator;
typedef __RBTreeIterator<T, const T&, const T*> const_iterator;
public:
RBTree()
:_root(nullptr)
{}
~RBTree()
{
_Destory(_root);
_root = nullptr;//好习惯
}
iterator begin()
{
Node* cur = _root;
while (cur != nullptr && cur->_left != nullptr)//目的:找最左结点
{
cur = cur->_left;
}
return iterator(cur);//调用迭代器类中的结点构造函数,构造一个Node结点
}
iterator end()
{
return iterator(nullptr);//注意:end是最后一个结点的下一个数据,所以直接用空去构造就行了
}
const_iterator begin()const
{
Node* cur = _root;
while (cur != nullptr && cur->_left != nullptr)
{
cur = cur->_left;
}
return const_iterator(cur);
}
const_iterator end()const
{
return const_iterator(nullptr);
}
Node* Find(const K& key)
{
Node* cur = _root;
KeyOfT kot;
while (cur != nullptr)
{
if (kot(cur->_data) > key)//表示的就是使用KeyOfT去定义一个对象,帮助我们取出对应模板类型的data数据,本质是在调用()这个仿函数
{
cur = cur->_left;
}
else if (kot(cur->_data) < key)
{
cur = cur->_right;
}
else
{
return cur;
}
}
return nullptr;
}
pair<iterator,bool> Insert(const T& data)//此时一定要支持map实现方括号,实现方括号就涉及到插入接口
{
if (_root == nullptr)
{
_root = new Node(data);
_root->_color = BLACK;
return make_pair(iterator(_root), true);//注意:方括号的返回值一定是返回两个量,一个是迭代器的地址,一个是bool值,值得注意的是,迭代器的地址中对于map来说就是一个pair结构体
}
KeyOfT kot;
Node* cur = _root;
Node* parent = nullptr;
while (cur != nullptr)
{
if (kot(cur->_data) < kot(data))
{
parent = cur;
cur = cur->_right;
}
else if (kot(cur->_data) > kot(data))
{
parent = cur;
cur = cur->_left;
}
else
{
return make_pair(iterator(cur), false);
}
}
cur = new Node(data);//此时默认初始化的时候,创建的就是一个红色结点
Node* newnode = cur;//此时因为cur会不断的迭代,所以这个位置需要先保存一下
//cur->_color = RED;
if (kot(parent->_data) > kot(data))
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
cur->_parent = parent;
while (parent != nullptr && parent->_color == RED)//因为变色可能会一直向上,直到遇到root结点,所以需要判断到root结点,也就是parent=nullptr的时候
{
//根据原理:1.将父结点和叔叔结点变成黑色,爷爷结点变成黑色(前提是uncle不为空)
Node* pparent = parent->_parent;
if (pparent->_left == parent)//叔叔结点需要判断左右
{
Node* uncle = pparent->_right;
//此时就找到叔叔结点了,根据原理,此时就需要进行判断
if (uncle != nullptr && uncle->_color == RED)
{
//(uncle存在且为红)满足该条件,就走自己的变色规则(parent和uncle变红,pparent变黑)就行
parent->_color = BLACK;
uncle->_color = BLACK;
pparent->_color = RED;
//搞定完之后,再根据原理,需要判断爷爷结点的父结点是红色还是黑色(迭代循环走走)
cur = pparent;
parent = cur->_parent;
//parent = pparent->_parent;//这种写法虽然更快,但是没有真正按照迭代的原理来,每一步都要按照原理来最好,容易看懂
}
else
{
if (parent->_left == cur)
{
//满足该条件就是一个单旋
RotateR(pparent);
parent->_color = BLACK;
pparent->_color = RED;
}
else
{
//双旋
RotateL(parent);
RotateR(pparent);
cur->_color = BLACK;//双旋会导致cur去做根,所以cur变黑,单旋由于parent做根,所以parent变黑
pparent->_color = RED;
//上面两步就是双旋变色的关键,下面这个变色可有可无
parent->_color = RED;//这个只是为了保持红色而已,本质上没有变,最终让代码还可以进入循环进行判断,防止有的场景问题
}
break;//单旋或者双旋完,此时该子树的颜色就正常了,就可以退出该循环了
}
}
else
{
Node* uncle = pparent->_left;
if (uncle != nullptr && uncle->_color == RED)//同理
{
//符合变色规则,就开始变色
parent->_color = BLACK;
uncle->_color = BLACK;
pparent->_color = RED;
cur = pparent;
parent = cur->_parent;
//parent = pparent->_parent;//最好不要这样写,因为这样写,会导致cur的位置没有改变,迭代不了cur,只迭代了parent
}
else
{//两个场景是类似的,可以当作一个场景看
if (parent->_right == cur)
{
RotateL(pparent);
parent->_color = BLACK;
pparent->_color = RED;
}
else
{
RotateR(parent);
RotateL(pparent);
cur->_color = BLACK;
pparent->_color = RED;
}
break;
}
}
}
_root->_color = BLACK;//此时就可以不需要判断,某个根结点的父结点是否为空,因为如果爷爷结点的父结点为黑色了,这个循环就会被终止,这步就是多余的,但是如果是真的走到了root结点,root结点被置红了,那么循环终止的这个代码就尤为重要
return make_pair(iterator(newnode), true);//因为会迭代,所以需要使用newnode,不能使用cur
}
private:
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
Node* pparent = parent->_parent;
parent->_right = subRL;
if (subRL != nullptr)
{
subRL->_parent = parent;
}
subR->_left = parent;
parent->_parent = subR;
if (pparent == nullptr)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (pparent->_left == parent)
{
pparent->_left = subR;
}
else
{
pparent->_right = subR;
}
subR->_parent = pparent;
}
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
Node* pparent = parent->_parent;
parent->_left = subLR;
if (subLR != nullptr)
{
subLR->_parent = parent;
}
subL->_right = parent;
parent->_parent = subL;
if (pparent == nullptr)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
if (pparent->_left == parent)
{
pparent->_left = subL;
}
else
{
pparent->_right = subL;
}
subL->_parent = pparent;
}
}
public:
void _Destory(Node* root)
{
if (root == nullptr)
{
return;
}
_Destory(root->_left);
_Destory(root->_right);
delete root;
}
void InOrder()//中序打印AVL树
{
_InOrder(_root);
cout << endl;
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
else
{
_InOrder(root->_left);//这边递归不要传参,你真的是人才啊
cout << root->_kv.first << " ";
_InOrder(root->_right);
}
}
private:
Node* _root;
};












![[web安全原理分析]-XXE漏洞入门](https://img-blog.csdnimg.cn/img_convert/87bc77829c2efb9ea1d2d3c17e0d7910.png)