目录
一、树简介
二、二叉树
1、简介
2、二叉树的性质
3、满二叉树和完全二叉树
三、二叉树的遍历
四、二叉树遍历代码实现
五、二叉搜索树(Binary Search Tree)
1、简介
2、二插搜索树的局限性
六、平衡二叉搜索树(AVL树)
七、红黑树(Red-Black Tree)
1、简介
2、性质
3、使用场景
八、B树(B-Tree)
1、简介
2、特点
九、B+树
1、简介
2、B+的特性
3、稠密索引
4、稀疏索引
一、树简介
树是一种非线性的数据结构,是由n(n >=0)个结点组成的有限集合。
如果n==0,树为空树。如果n>0,树有一个特定的结点,叫做根结点(root)。根结点只有直接后继,没有直接前驱
除根结点以外的其他结点划分为m(m>=0)个互不相交的有限集合,T0,T1,T2,...,Tm-1,每个集合都是一棵树,称为根结点的子树(sub tree)。
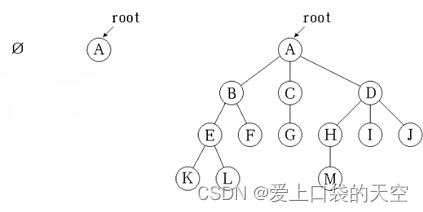
下面是一些其它基本概念:
- 节点的度:节点拥有的子树个数
- 叶子节点(leaf):度为0的节点,也就是没有子树的节点
- 树的高度:树中节点的最大层数,也叫做树的深度
二、二叉树
1、简介
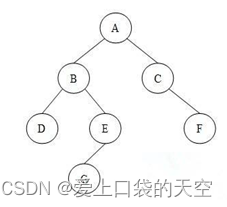
对于树这种数据结构,使用最频繁的是二叉树。
每个节点最多只有2个子节点的树,叫做二叉树。二叉树中,每个节点的子节点作为根的两个子树,一般叫做节点的左子树和右子树。
2、二叉树的性质
- 若二叉树的层次从0开始,则在二叉树的第i层至多有2^i个结点(i>=0)
- 高度为k的二叉树最多有2^(k+1) - 1个结点(k>=-1)(空树的高度为-1)
- 对任何一棵二叉树,如果其叶子结点(度为0)数为m, 度为2的结点数为n, 则m = n + 1
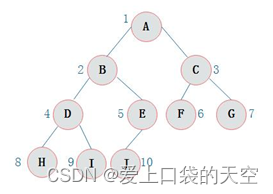
3、满二叉树和完全二叉树
- 满二叉树:除了叶子节点外,每个节点都有两个子节点,每一层都被完全填充。
- 完全二叉树:除了最后一层外,每一层都被完全填充,并且最后一层所有节点保持向左对齐。
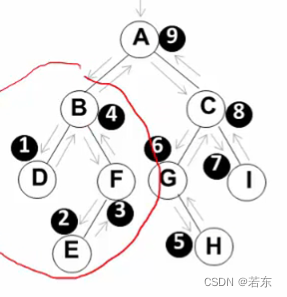
三、二叉树的遍历
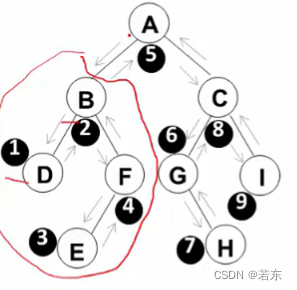
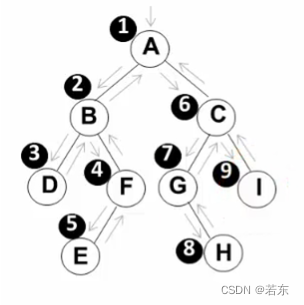
- 中序遍历:即左-根-右遍历,对于给定的二叉树根,寻找其左子树;对于其左子树的根,再去寻找其左子树;递归遍历,直到寻找最左边的节点i,其必然为叶子,然后遍历i的父节点,再遍历i的兄弟节点。随着递归的逐渐出栈,最终完成遍历
- 先序遍历:即根-左-右遍历
- 后序遍历:即左-右-根遍历
- 层序遍历:按照从上到下、从左到右的顺序,逐层遍历所有节点。
四、二叉树遍历代码实现
package com.kgf.algorithm.tree;
import java.util.ArrayDeque;
import java.util.Queue;
/***
* 二叉树的遍历
*/
public class TreeErgodic {
public static void main(String[] args) {
TreeNode root = new TreeNode(1);
TreeNode tn1 = new TreeNode(3);
TreeNode tn2 = new TreeNode(5);
TreeNode tn3 = new TreeNode(2);
TreeNode tn4 = new TreeNode(7);
TreeNode tn5 = new TreeNode(6);
root.left=tn1;
root.right=tn2;
tn1.left = tn3;
tn1.right = tn4;
tn2.left = tn5;
TreeErgodic te = new TreeErgodic();
te.levelTraversal2(root);
}
/***
* 层序遍历
* 按照从上到下、从左到右的顺序,逐层遍历所有节点。
* 结果是:1 3 5 2 7 6
* @param treeNode
*/
public void levelTraversal2(TreeNode treeNode){
//创建一个队列,先进先出
Queue<TreeNode> queue = new ArrayDeque();
queue.add(treeNode);
while (!queue.isEmpty()){
TreeNode node = queue.poll();
System.out.print(node.val+"\t");
if (node.left!=null){
queue.add(node.left);
}
if (node.right!=null){
queue.add(node.right);
}
}
}
/***
* 层序遍历
* 按照从上到下、从左到右的顺序,逐层遍历所有节点。
* 结果是:1 3 5 2 7 6
* @param treeNode
*/
public void levelTraversal(TreeNode treeNode){
//创建一个队列,先进先出
Queue queue = new ArrayDeque();
queue.add(treeNode.val);
loadTreeNode(treeNode,queue);
while (!queue.isEmpty()){
System.out.print(queue.poll()+"\t");
}
}
private void loadTreeNode(TreeNode treeNode, Queue queue) {
if (treeNode==null)return;
if (treeNode.left!=null){
queue.add(treeNode.left.val);
}
if (treeNode.right!=null){
queue.add(treeNode.right.val);
}
loadTreeNode(treeNode.left,queue);
loadTreeNode(treeNode.right,queue);
}
/***
* 后序遍历
* 即左-右-根遍历
* 结果是:2 7 3 6 5 1
* @param treeNode
*/
public void afterOrder(TreeNode treeNode){
if (treeNode==null)return;
afterOrder(treeNode.left);
afterOrder(treeNode.right);
System.out.print(treeNode.val+"\t");
}
/***
* 中序遍历
* 即左-根-右遍历
* 结果是:2 3 7 1 6 5
* @param treeNode
*/
public void centerOrder(TreeNode treeNode){
if (treeNode==null)return;
centerOrder(treeNode.left);
System.out.print(treeNode.val+"\t");
centerOrder(treeNode.right);
}
/***
* 先序遍历
* 即根-左-右遍历
* 结果是:1 3 2 7 5 6
* @param treeNode
*/
public void preOrder(TreeNode treeNode){
if (treeNode==null)return;
System.out.print(treeNode.val+"\t");
preOrder(treeNode.left);
preOrder(treeNode.right);
}
}
五、二叉搜索树(Binary Search Tree)
1、简介
二叉搜索树也称为有序二叉查找树,满足二叉查找树的一般性质,是指一棵空树具有如下性质:
- 任意节点左子树如果不为空,则左子树中节点的值均小于根节点的值
- 任意节点右子树如果不为空,则右子树中节点的值均大于根节点的值
- 任意节点的左右子树,也分别是二叉搜索树
- 没有键值相等的节点
基于二叉搜索树的这种特点,在查找某个节点的时候,可以采取类似于二分查找的思想,快速找到某个节点。n 个节点的二叉查找树,正常的情况下,查找的时间复杂度为 O(logN)。
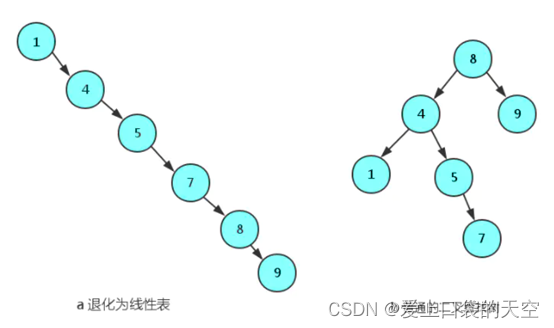
2、二插搜索树的局限性
一个二叉搜索树是由n个节点随机构成,所以,对于某些情况,二叉查找树会退化成一个有n个节点的线性链表。如下图:
六、平衡二叉搜索树(AVL树)
通过二叉搜索树的分析我们发现,二叉搜索树的节点查询、构造和删除性能,与树的高度相关,如果二叉搜索树能够更“平衡”一些,避免了树结构向线性结构的倾斜,则能够显著降低时间复杂度。
平衡二叉搜索树:简称平衡二叉树。由前苏联的数学家Adelse-Velskil和Landis在1962年提出的高度平衡的二叉树,根据科学家的英文名也称为AVL树。
它具有如下几个性质:
- 可以是空树
- 假如不是空树,任何一个结点的左子树与右子树都是平衡二叉树,并且高度之差的绝对值不超过1
平衡的意思,就是向天平一样保持左右水平,即两边的分量大约相同。如定义,假如一棵树的左右子树的高度之差超过1,如左子树的树高为2,右子树的树高为0,子树树高差的绝对值为2就打破了这个平衡。
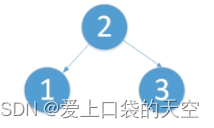
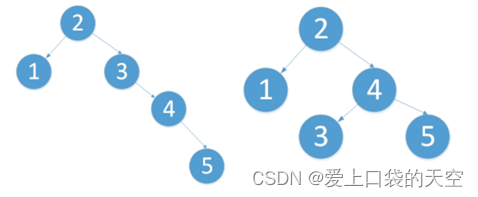
比如,依次插入1,2,3三个结点后,根结点的右子树树高减去左子树树高为2,树就失去了平衡。我们希望它能够变成更加平衡的样子。
AVL树是带有平衡条件的二叉搜索树,它是严格的平衡二叉树,平衡条件必须满足(所有节点的左右子树高度差不超过1)。不管我们是执行插入还是删除操作,只要不满足上面的条件,就要通过旋转来保持平衡,而旋转是非常耗时的。旋转的目的是为了降低树的高度,使其平衡。
AVL树适合用于插入删除次数比较少,但查找多的情况。也在Windows进程地址空间管理中得到了使用。
七、红黑树(Red-Black Tree)
1、简介
红黑树是一种特殊的二叉查找树。红黑树的每个节点上都有存储位表示节点的颜色,可以是红(Red)或黑(Black)。
2、性质
- 节点是红色或黑色
- 根节点是黑色
- 每个叶子节点都是黑色的空节点(NIL节点)。
- 每个红色节点的两个子节点都是黑色(从每个叶子到根的所有路径上不能有两个连续的红色节点)
- 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点
在插入一个新节点时,默认将它涂为红色(这样可以不违背最后一条规则),然后进行旋转着色等操作,让新的树符合所有规则。
红黑树也是一种自平衡二叉查找树,可以认为是对AVL树的折中优化。
3、使用场景
红黑树多用于搜索,插入,删除操作多的情况下。红黑树应用比较广泛:
- 广泛用在各种语言的内置数据结构中。比如C++的STL中,map和set都是用红黑树实现的。Java中的TreeSet,TreeMap也都是用红黑树实现的。
- 著名的linux进程调度Completely Fair Scheduler,用红黑树管理进程控制块。
- epoll在内核中的实现,用红黑树管理事件块
- nginx中,用红黑树管理timer等
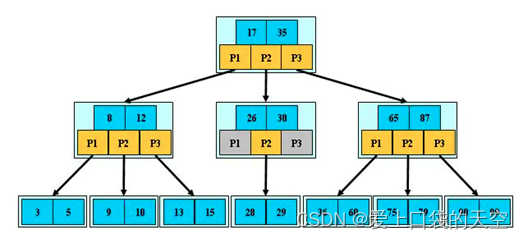
八、B树(B-Tree)
1、简介
B树(B-Tree)是一种自平衡的树,它是一种多路搜索树(并不是二叉的),能够保证数据有序。同时,B树还保证了在查找、插入、删除等操作时性能都能保持在O(logn),为大块数据的读写操作做了优化,同时它也可以用来描述外部存储。
2、特点
- B树可以定义一个M值作为预定范围,即M路(阶)B树,每个节点最多有M个孩子;且M>2
- 根结点的儿子数为[2, M]
- 除根结点以外的非叶子结点的儿子数为[M/2, M]
- 每个结点存放至少M/2-1(取上整)和至多M-1个关键字;(至少2个key)
- 非叶子结点的关键字个数 = 指向儿子的指针个数 – 1
- 非叶子结点的关键字:K[1], K[2], …, K[M-1];且K[i] < K[i+1]
- 非叶子结点的指针:P[1], P[2], …, P[M],其中P[1]指向关键字小于K[1]的子树,P[M]指向关键字大于K[M-1]的子树,其它P[i]指向关键字属于(K[i-1], K[i])的子树
- 所有叶子结点位于同一层
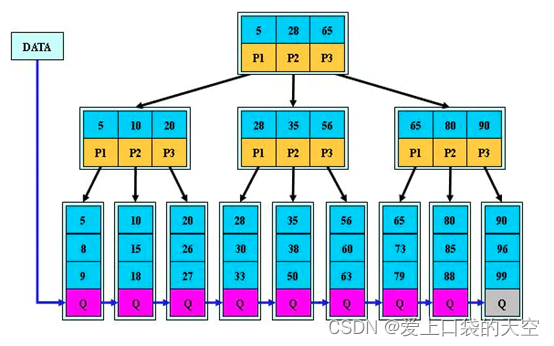
九、B+树
1、简介
B+树是B-树的变体,也是一种多路搜索树。
B+的搜索与B-树也基本相同,区别是B+树只有达到叶子结点才命中(B-树可以在非叶子结点命中),其性能也等价于在关键字全集做一次二分查找。
2、B+的特性
- 所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好是有序的
- 不可能在非叶子结点命中
- 非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层
- 更适合文件索引系统
3、稠密索引
稠密索引,即每一条记录,对应一个索引字段。稠密索引,访问速度非常块,但是维护成本大。根据索引字段不一样,有候选键索引和非候选键索引之分 。
4、稀疏索引
- 相对稠密索引,稀疏索引并没有每条记录,建立了索引字段,而是把记录分为若干个块,为每个块建立一条索引字段
- 稀疏索引字段,要求索引字段是按顺序排序的,否则无法有效索引
稀疏索引是如何进行定位的呢?
- 假设需要搜索字段值为K的记录,那先检索出比K小的最大值索引字段,再根据该字段所在的记录集合,进行顺序查找,直到找到记录K。
- 稀疏索引,数据查询速度较慢,但是存储空间小,维护成本低
那么如何设置索引字段呢?
- 既然索引是为了提高访问速度,简单说,要是一些数据经常被使用、被查询,那这些字段就应该设置索引