算法框架

对于回溯算法框架。其实解决一个回溯问题，实际上就是一个决策树的遍历过程。

这也就是为什么在刷算法题之前，一定要从树的题目开始刷，后期可以很方便的树立使用递归求解问题的思路。

一般需要你明确三个元素：

路径：当前已经做出的选择是哪些
选择列表：也就是你可以做出的选择
结束条件：到达树的底部，没有办法在做出的选择。

对于这三个概念，在后面的分析中，会反复的进行提及。
代码方面：

result = [] 
int[] path = new int[n]; // 路径
boolean[] st = new boolean[n]; // 是否被使用过
void dfs(当前遍历的位置){
	if(满足结束条件){
		result.add(路径);
		return;
	}
	for(int i = 0; i < 元素个数； i++){
		if(没有被使用过){
			做选择
			dfs(当前遍历的位置 + 1)
			撤销选择
		}
	}
}

其核心就是 for 循环里面的递归，回溯是一种特殊的DFS算法，在递归调用之前「做选择」，在递归调用之后「撤销选择」。

下面我们来分析一下全排列的问题，深化上面的概念：
什么是全排列问题，这边不在进行介绍，为了简化问题的概念，直接讨论的全排列问题不包含重复的数字。

如果没有计算机，我们自己该如何做一个集合的全排列呢？一般对于[1,2,3]问题：
先固定第一位为 1，然后第二位可以是 2，那么第三位只能是 3；然后可以把第二位变成 3，第三位就只能是 2 了；然后就只能变化第一位，变成 2，然后再穷举后两位

算法其实也可以这样求解，
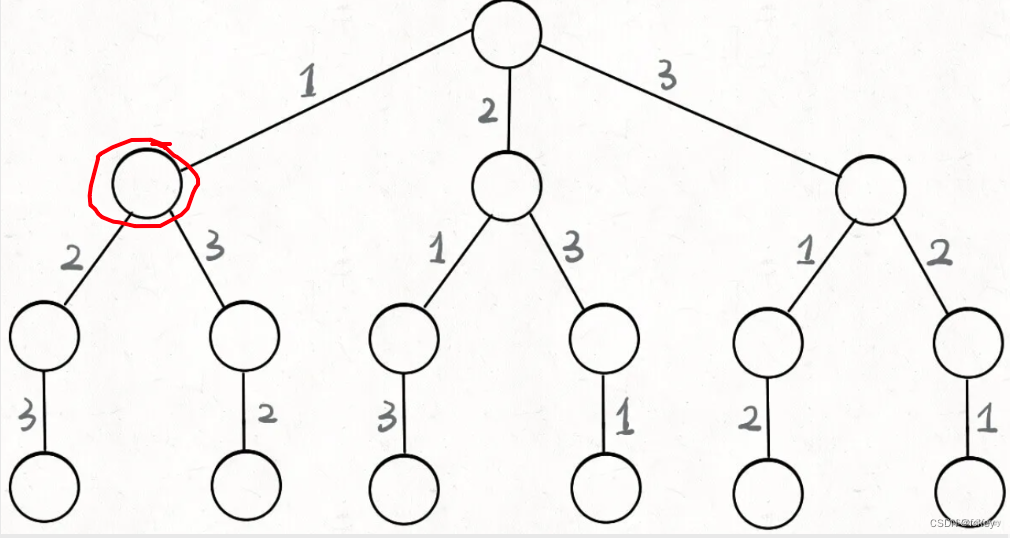
在这里插入图片描述
对于一些不满足条件题目条件的点，都进行删除，最后得到下面这颗树。

很明显，这其实就是一个多叉树的问题。而且对于树上的每一个节点都需要进行判断，才能继续下一步

为什么这样说？应为我们要求的是全排列的问题，对于图中红圈的点，之后的所有路径的选择都是需要排除掉1的。所以，对于每一个node，都需要进行判断。

按照上述的说明不满足条件题目条件的点，我们再来看一下具体是怎么操作的，为了更好的理解，我们把上述做决策的过程完全打开。

void dfs(node){
	// 1. 结束条件和存储结果 
	//2. 对于不符合结束条件的节点，我们应该对每一个节点都判断一下，形式如下
	if(node1 符合题目条件) {
		node(1) 访问node1, 递归操作
	}
	if(node2 符合题目条件) {
		node(2) 访问node2, 递归操作
	}
	if(node3 符合题目条件) {
		node(3) 访问node1, 递归操作
	}
	.....
}

那么也就是说明，当前层的满足条件的节点就会被记录下来，按照多叉树的遍历形式，里面呈现的就是一个for循环的格式。

但是，还有一个问题就是，一个决策树在同层直接涉及到的数据污染问题怎么解决。

比如：从袋子里面摸球问题，第一次你摸了1，如果从头开始摸球的话，需要把1号球给放入，然后摸出2号球。

如下图所示：
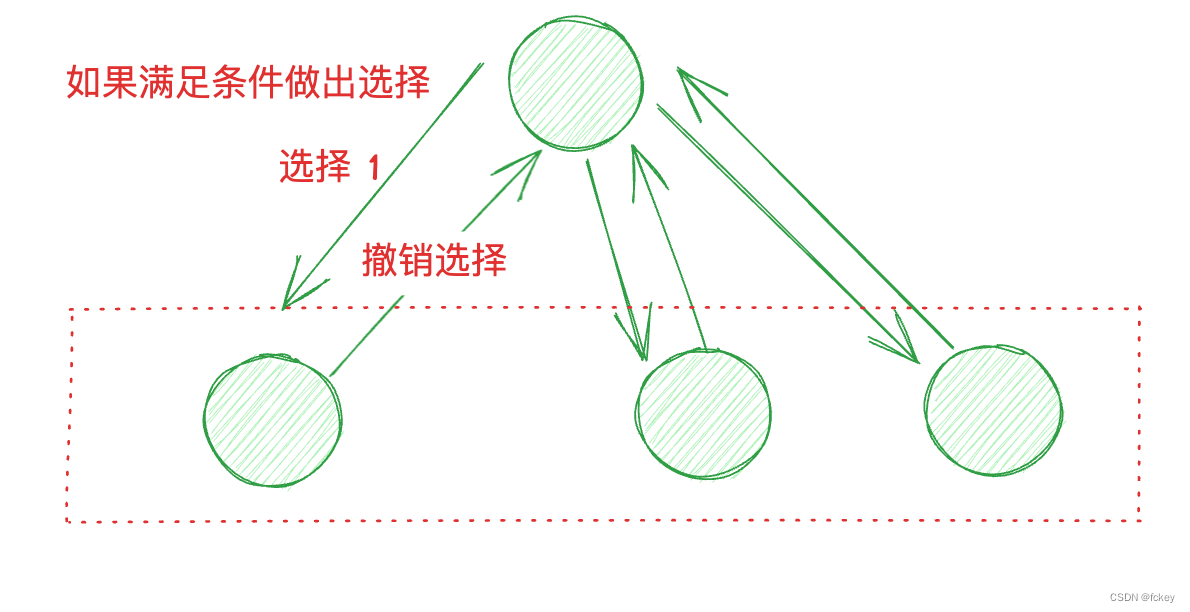
在这里插入图片描述
所以，我们需在在选择节点之后，对当前节点进行撤销选择才行，所以上述代码变为

void dfs(node){
	// 1. 结束条件和存储结果 
	//2. 对于不符合结束条件的节点，我们应该对每一个节点都判断一下，形式如下
	if(node1 符合题目条件) {
		// 标识已经对当前节点的访问
		标识节点做了选择
		node(1) 访问node1, 递归操作
		取消当前节点，设为没有选择状态
	}
	if(node2 符合题目条件) {
		标识节点做了选择
		node(2) 访问node2, 递归操作
		取消当前节点，设为没有选择状态
	}
	if(node3 符合题目条件) {
		标识节点做了选择
		node(3) 访问node1, 递归操作
		取消当前节点，设为没有选择状态
	}
	.....
}

也就是说，对于当前决策树中的所有节点，
在这里插入图片描述
对于递归的板子，里面的for循环就是横向移动，而对于for循环中的递归就是纵向移动，不断的深入到底部的过程。
让我们来看看全排列的代码：

import java.util.*;
import java.io.*;

class Main{
    static int N = 10;
    static int[] path = new int[N]; // 用来记录当前的路径 
    static boolean[] sta = new boolean[N]; //用来记录当前已经填了哪些数字
    // u代表当前已经填到了哪位
    public static void dfs(int u, int n){
        if(u == n){
            for(int i = 0; i < n; i ++) System.out.print(path[i] + " ");
            System.out.println();
            return;
        }
        // 对所有节点都看一下，如果符合条件的自然会拿出来
        for(int i = 1; i <= n; i ++){
            // 先判断当前数字是否已经被使用过
            if(!sta[i]){
                path[u] = i;
                sta[i] = true;
                dfs(u + 1, n);
                // 恢复现场
                sta[i] = false;
            }
        }
    }
    
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        dfs(0, n);
    }
}