👂 梦寻古镇 - 羽翼深蓝Wings - 单曲 - 网易云音乐

👂 如果我有一个男朋友 - 于娜懿 - 单曲 - 网易云音乐

👂 对酒（女生版） - 浅影阿 - 单曲 - 网易云音乐

👂 知我（抒情版） - 尘ah. - 单曲 - 网易云音乐

👂 骏马赞 (重新录制) - 九宝乐队 - 单曲 - 网易云音乐

终于要开始算法入门了，学完再刷点题，应该就是算法小白了吧

别人大一下都会哈夫曼，平衡二叉树，启发式这些东西了，好好加油，分配好注意力

最近还了解到字节青训营，加入首先要笔试，考算法+八股，那我就先攻克算法吧

（企业员工手把手教你做项目~差的有点远，先好好打基础）

不必妄自菲薄，很多学了几年，也只会黑框输入的大有人在，什么时候开始都不晚

目录

🏆算法之美

🌳算法的优劣

🌳复杂度计算方法

🏆贪心算法

🌳贪心本质

🌳最优装载问题

🏆贪心刷题

🌳1832: [NewOJ Week 9] 配对

🌳1785: [NewOJ Contest 10] 剪绳子

🌳P1589 泥泞路

🌳P1208 [USACO1.3]混合牛奶 Mixing Milk

🌳P4995 跳跳！

🌳P1094 [NOIP2007 普及组] 纪念品分组

🌳P1199 [NOIP2010 普及组] 三国游戏

🌳P2672 [NOIP2015 普及组] 推销员

🌳P1080 [NOIP2012 提高组] 国王游戏

🏆总结

---

洛谷官方题单

一个动态更新的洛谷综合题单 - Studying Father's luogu blog - 洛谷博客

🏆算法之美

🌳算法的优劣

以斐波那契数列举例

1，按照数列表达式，递归（7秒出结果）

#include<iostream>
using namespace std;

long double fib1(int n)
{
    if(n < 1)
        return -1;
    else if(n == 1 || n == 2)
        return 1;
    else
        return fib1(n - 1) + fib1(n - 2);
}

int main()
{
    int n;
    cin>>n;
    cout<<fib1(n);

    return 0;
}

45
1.1349e+009

2，数组存储每一项，从前往后递推，非递归（瞬间出结果）

#include<iostream>
using namespace std;

long double fib2(int n)
{
    long double temp;
    if(n < 1) return -1;
    //new动态分配内存, 创建数组, 首地址赋值给指针变量a
    long double *a = new long double[n + 1];
    a[1] = 1, a[2] = 1;
    for(int i = 3; i <= n; ++i)
        a[i] = a[i - 1] + a[i - 2];
    temp = a[n];
    delete []a; //释放数组所占内存
    return temp;
}

int main()
{
    int n;
    cin>>n;
    cout<<fib2(n);

    return 0;
}

45
1.1349e+009

总结

除了时间，空间复杂度，就是算法健壮性

何谓健壮性：算法对非法数据及操作有较好的反应和处理，eg: 信息管理系统中登记电话号码时，少数如1位，系统就应该提示出错 

补充：时间复杂度，并不是真的计算运行时间，而是将算法基本运算的执行次数，作为标准

🌳复杂度计算方法

时间复杂度：高效率

举例1

int sum(int n) {
    int sum = 0; //1次
    for(int i = 0; i <= n; ++i) //n + 1次
        sum += i; //n次
    return sum; //1次
}

执行次数为2n + 3，T(n) = 2*n + 3，当n足够大，舍去小项和系数，所以时间复杂度为O(n)

举例2

sum = 0; //1次
total = 0; //1次
for(i = 1; i <= n; ++i) { //n + 1次, 最后一次判断条件不成立，结束
    sum = sum + i; //n次
    for(j = 1; j <= n; ++j) //n*(n + 1)次
        total = total + i*j; //n * n次
}

计算贡献最大的语句即可，也就是O(n^2)

类似排序，插入，查找等算法，不能直接计算运行次数，可以按最好，最坏，平均3种情况求算法渐进复杂度

当然，通常只看最坏复杂度，它对于衡量算法好坏，具有实际意义 

空间复杂度：低存储

空间复杂度 = 输入输出数据 + 算法本身 + 额外的辅助空间

其中，辅助空间是衡量空间复杂度的关键

举例1

swap(int x, int y) { //x与y交换
    int temp;
    temp = x; //temp为辅助空间
    x = y;
    y = temp;
}

上述空间复杂度为O(1)

举例2

递归中，每次递归都需要一个栈空间来保存调用记录，因此计算空间复杂度时

需要计算递归栈的辅助空间

以计算n的阶乘为例

long long fac(int n) {
    if(n < 0) return -1;
    else if(n == 0 || n == 1) return 1;
    else return n * fac(n - 1);
}

递推 + 回归在系统内部使用栈实现，栈空间的大小为递归树的深度，如下图

计算n的阶乘时，递归树的深度为n，

所以n阶乘递归算法的空间复杂度为O(n)

具体分析 + 形象举例

常见算法时间复杂度：

1，常数阶：O(1)     

2，对数阶：O(logn), O(nlogn)

3，多项式阶：O(n), O(n^2), O(n^3)

4，指数阶：O(2^n), O(n!), O(n^n)

1 < logn < n < nlogn < n^2 < n^3 < 2^n < n! < n^n

关于复杂度的形象解释

一天 ≈ 10^5秒，一年 ≈ 3 * 10^7秒，100年 ≈ 3 * 10^9，三生三世 ≈ 10^10秒

假设有10亿数据排序，10亿 = 10^9

普通PC：10^9次运算每秒，

当复杂度O(n^2)，(10^9)^2 = 10^18，需要10^18 / 10^9 = 10^9秒 ≈ 30年

当复杂度O(nlogn)，需要10^9 * log10^9 / 10^9 ≈ 30秒（计算机一般用二进制，此处对数的底数也是二进制，所以log10 ≈ 3，3 * 9 ≈ 30）

超级计算机：10^17次 / 秒

复杂度O(n^2)需要10秒

复杂度O(nlogn)需要3 * 10^-7秒 

注意：2^10 = 1024 ≈ 10^3，2^30 ≈ 10^9，log10^3 ≈ log2^10 ≈ 10，log10^9 ≈ log2^30 ≈ 30

🏆贪心算法

🌳贪心本质

使用前提：1，贪心选择性质；；；2，最优子结构性质

贪心选择性质：

整体最优解，可以用一系列局部最优解表示。

应用同一规则，将原问题变为一个相似的，规模更小的子问题，而后的每一步都是当前最优选择，这种选择依赖于已做出的选择。

贪心解决的问题在程序运行中，无回溯过程

最有子结构性质：

一个问题的最优解包含其子问题的最优解。

例如S = {a1, a2, ..., ai, ..., an}，通过贪心选出一个当前最优解{ai}后，转化为求解子问题S-{ai}，如果原问题的最优解包含子问题的最优解，则说明该问题满足最优子结构性质

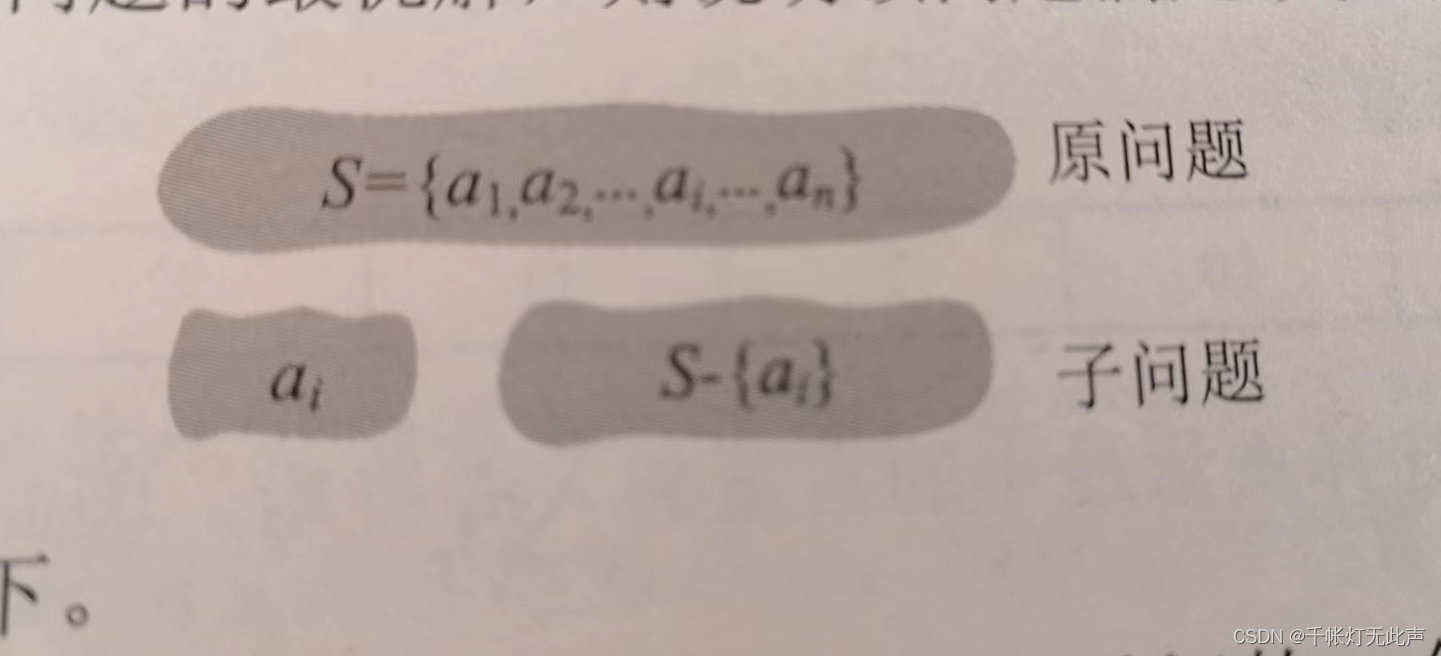
求解步骤：

（1）贪心策略

指定贪心策略，选择当前看上去最好的一个。

比如挑选苹果，如果你认为个头大的是最好的，那么每次都从苹果堆选一个最大的作为局部最优解，贪心策略就是选择当前最大的苹果。

如果你认为最红的苹果是最好的，那么每次都从苹果堆取一个最红的，贪心策略就是选择最红的苹果。

根据求解目标的不同，贪心策略也不同

（2）局部最优解

根据贪心策略，一步步得到局部最优解。

比如第1次选一个最大的苹果放起来，记为a1；

第2次再从剩下苹果选一个最大的苹果放起来，记为a2......

（3）全局最优解

把所有局部最优解合成原问题的一个最优解{a1, a2, ......}

🌳最优装载问题

有一天，海盗们截获了一艘装满各种各样古董的货船，每件古董都价值连城，一旦打碎就失去了价值。虽然海盗船足够大，但载重为c，每件古董重量为wi，海盗们绞尽脑汁要把尽可能多的宝贝装上船，该怎么办呢？

（看清题意，是装的数量最大，而非重量最大）

1，问题分析

装载的物品尽可能多（数量最多），船的容量固定，那么优先装重量小的物品。

采用重量最轻者先装，从局部最优达到全局最优。

2，算法设计

（1）载重定值为c，wi越小，可装载的古董数量n越大。依次选择最小重量古董，直到不能装入

（2）把n个古董按重量升序排序，根据贪心策略尽可能多的选出前i个古董，直到不能继续装入。

此时装入的古董数量就是全局最优解

3，完美图解

4，算法实现

用一维数组w[] 存储古董重量

（1）按重量升序排序，C++ sort()函数，头文件#include<algorithm>

sort(begin, end); 
//参数begin和end表示一个范围，分别为待排序数组的首地址和尾地址，默认升序

本例即sort(w, w + n);

（2）按照贪心策略找最优解

ans记录已装载数量，tmp代表装载到船上的古董重量，两个变脸初始化为0...

依次检查每个古董，tmp += 该古董重量，<= 载重c，则令ans++，否则退出

double tmp = 0.0;
int ans = 0; //tmp已装载总重量，ans为已装载个数
for(int i = 0; i < n; ++i) {
    tmp += w[i];
    if(tmp <= c)
        ans++;
    else 
        break;
}
cout<<ans<<endl;

5，算法分析

时间复杂度

sort函数平均时间复杂度O(nlogn)，输入和贪心策略求解的两个for语句的时间复杂度均为O(n)，总时间复杂度O(nlogn)

空间复杂度

程序中使用tmp, ans等辅助变量，空间复杂度O(1)

🏆贪心刷题

可以看看我当初刷的12道贪心题目（含链接和AC代码），当初啥也不会，结构体都不会，瞎折腾

(58条消息) C++蓝桥杯贪心算法_千帐灯无此声的博客-CSDN博客

下面是我从网上找的新题目

🌳1832: [NewOJ Week 9] 配对

P1832 - [NewOJ Week 9] 配对 - New Online Judge (ecustacm.cn)

标签：基础题，贪心

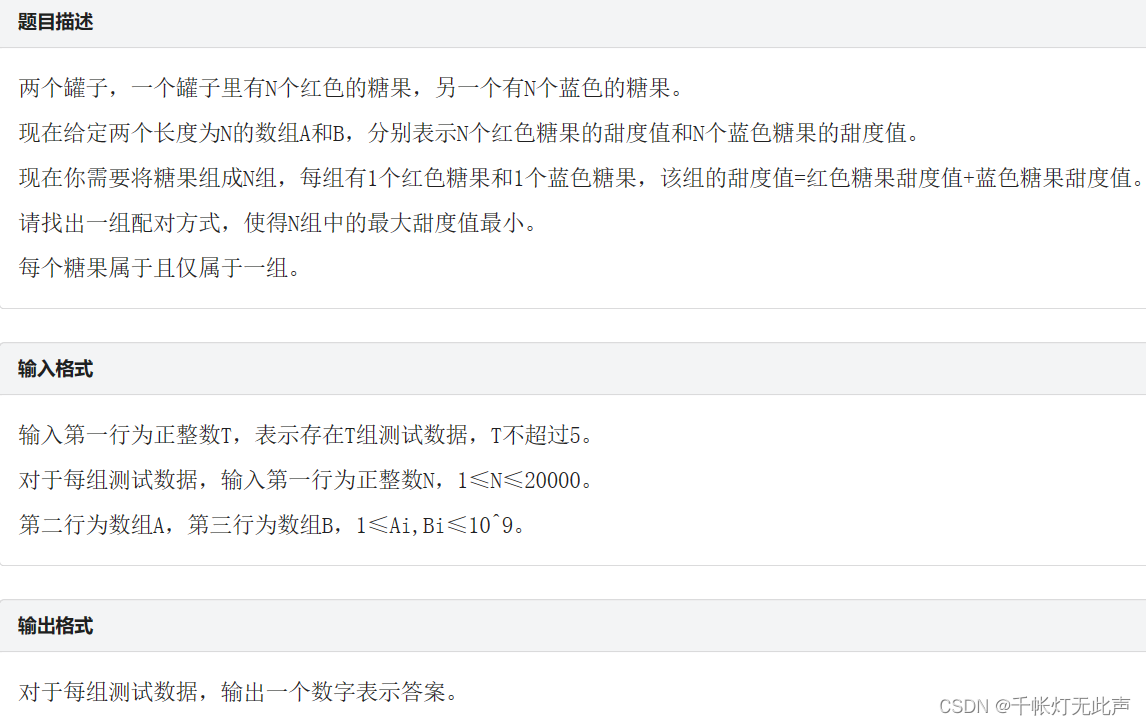
对A，B都升序排序，然后用当前A的最大值配对B的最小值，配对完这次后，这两个糖果就可以“丢掉了”，后续也是按这个规则，那么一系列局部最优解就能得出全局最优解

额外的测试

1
10
1 9 10 20 11 13 15 29 33 2
1 2 3 4 5 6 7 8 9 10
34

结果AC  0%，原来是多组测试，不要忘了第23行回车

cout<<Max<<endl; //回车不要忘, 多组测试

AC  代码

#include<iostream>
#include<algorithm> //sort()
using namespace std;
const int maxn = 2e4 + 10;
long long a[maxn], b[maxn];
int main()
{
    int t, n;
    cin>>t;
    while(t--) {
        cin>>n;
        for(int i = 0; i < n; ++i)
            cin>>a[i];
        for(int i = 0; i < n; ++i)
            cin>>b[i];
        sort(a, a + n);
        sort(b, b + n); //升序排序
        long long Max = 0;
        //最小的红糖果和最大的蓝糖果依次配对,
        //得到的最大甜度值最小
        for(int i = 0, j = n - 1; i < n; ++i, --j)
            Max = max(a[i] + b[j], Max); //取最大甜度
        cout<<Max<<endl; //输出最小的最大甜度
    }
    return 0;
}

🌳1785: [NewOJ Contest 10] 剪绳子

P1785 - [NewOJ Contest 10] 剪绳子 - New Online Judge (ecustacm.cn)

标签：基础题，贪心

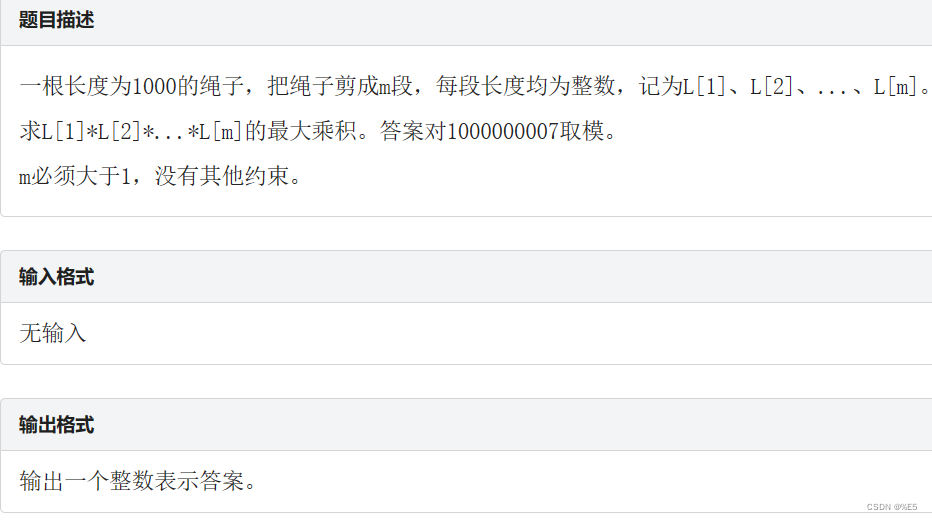
任意大于等于5的正整数，可以拆成2和3的组合，而且乘积还变大了

比如

2 = 2, 3 = 3, 4 = 2 + 2, 5 = 2 + 3, 6 = 3 + 3
7 = 3 + 2 + 2, 8 = 3 + 3 + 2, 9 = 3 + 3 + 3...

显而易见，3越多，乘积越大，比如3 * 3 * 2 > 2 * 2 * 2 * 2等等

至于证明，用到了算几不等式

显然1000个数，332个3，2个2刚刚好

1000 = 332 * 3 + 2 * 2，答案就是3^332 + 4

AC  代码

#include<iostream>
using namespace std;

int main()
{
    long long ans = 1;
    //边乘边取余
    for(int i = 0; i < 332; ++i)
        ans = ans * 3 % 1000000007; //3^332, 还剩4
    cout<<ans * 2 * 2 % 1000000007;
    return 0;
}

620946522

🌳P1589 泥泞路

P1589 泥泞路 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

标签：普及-，贪心，数学

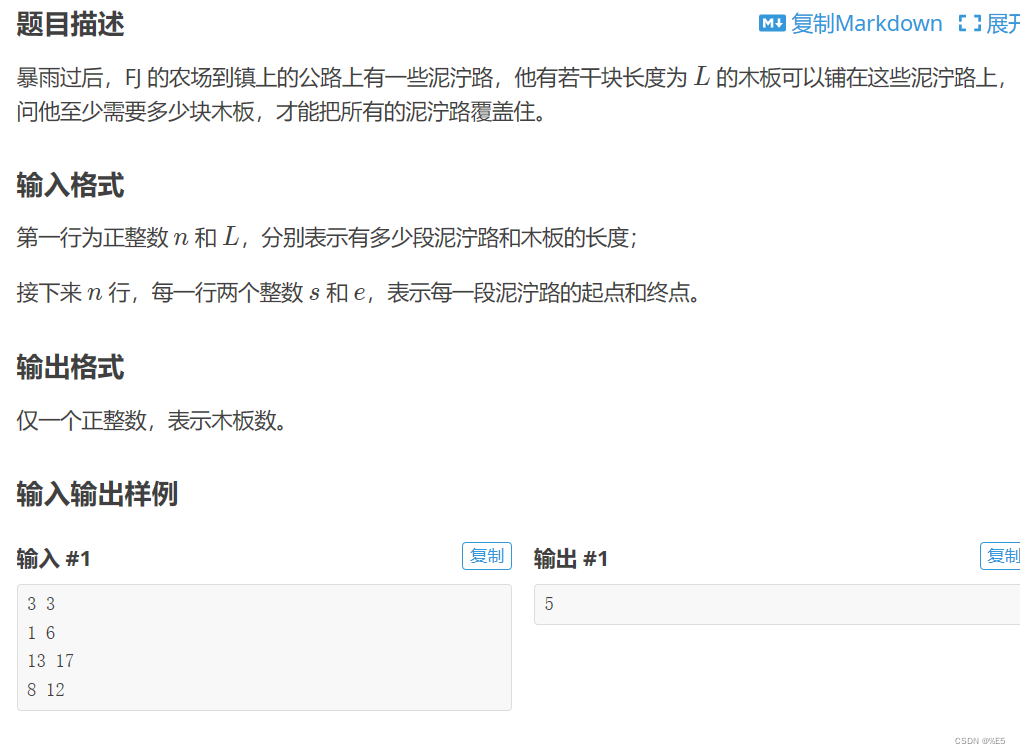
先小到大排序，按起点终点都行，由题意，泥路不存在重合

额外的测试

3 10
5 25
40 81
85 90
7

4 1000
1 28
33 104
104 111
1002 1003
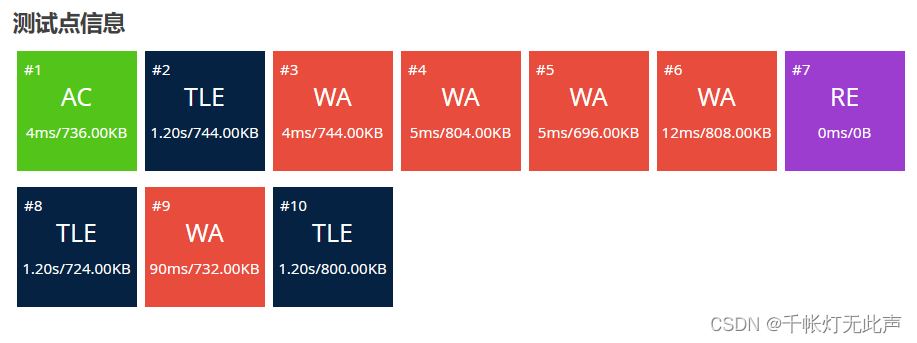
2

AC  60%  代码

调了很久才AC  60%

#include<iostream>
#include<algorithm>//sort()
using namespace std;
int ans; //需要的木板数

struct rode
{
    int fir, sec; //每段路起点, 终点
};

bool cmp(rode x, rode y)
{
    return x.fir < y.fir; //按起点升序排序
}

int main()
{
    struct rode a[10010];
    int n, L;
    cin>>n>>L;
    //输入n段泥泞的路
    for(int i = 0; i < n; ++i)
        cin>>a[i].fir>>a[i].sec;
    sort(a, a + n, cmp); //排序
    //遍历每一段路
    int len , num;
    for(int i = 0; i < n; ++i) {
        len = a[i].sec - a[i].fir; //泥路长度
        num = (len + L - 1) / L; //当前路段增加木板数
        ans += num;
        if(num != 0) //如果加了木板, 取较大值
            a[i + 1].fir = max(a[i + 1].fir, a[i].fir + L * num); //可能的新起点
    }
    cout<<ans;

    return 0;
}

我也不知道哪里错了，懒得debug了

换个思路：用now表示已经覆盖的最远距离，一块一块木板慢慢来

AC  代码

#include<iostream>
#include<algorithm>//sort()
using namespace std;
int ans; //需要的木板数

struct rode
{
    int fir, sec; //每段路起点, 终点
};

bool cmp(rode x, rode y)
{
    return x.fir < y.fir; //按起点升序排序
}

int main()
{
    struct rode a[10010];
    int n, L;
    cin>>n>>L;
    //输入n段泥泞的路
    for(int i = 0; i < n; ++i)
        cin>>a[i].fir>>a[i].sec;
    sort(a, a + n, cmp); //排序
    //遍历每一段路
    int now = a[0].fir; //now已经覆盖的最远距离
    for(int i = 0; i < n; ++i) {
        now = max(now, a[i].fir); //更新
        while(a[i].sec > now) { //泥路终点大于当前位置
            ans++;
            now += L; //当前位置前进一块木板的距离
        }
    }
    cout<<ans;

    return 0;
}

代码第29 - 31行，一块一块木板来，防止漏掉某些情况 

🌳P1208 [USACO1.3]混合牛奶 Mixing Milk

P1208 [USACO1.3]混合牛奶 Mixing Milk - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

标签：贪心，USACO，普及- 

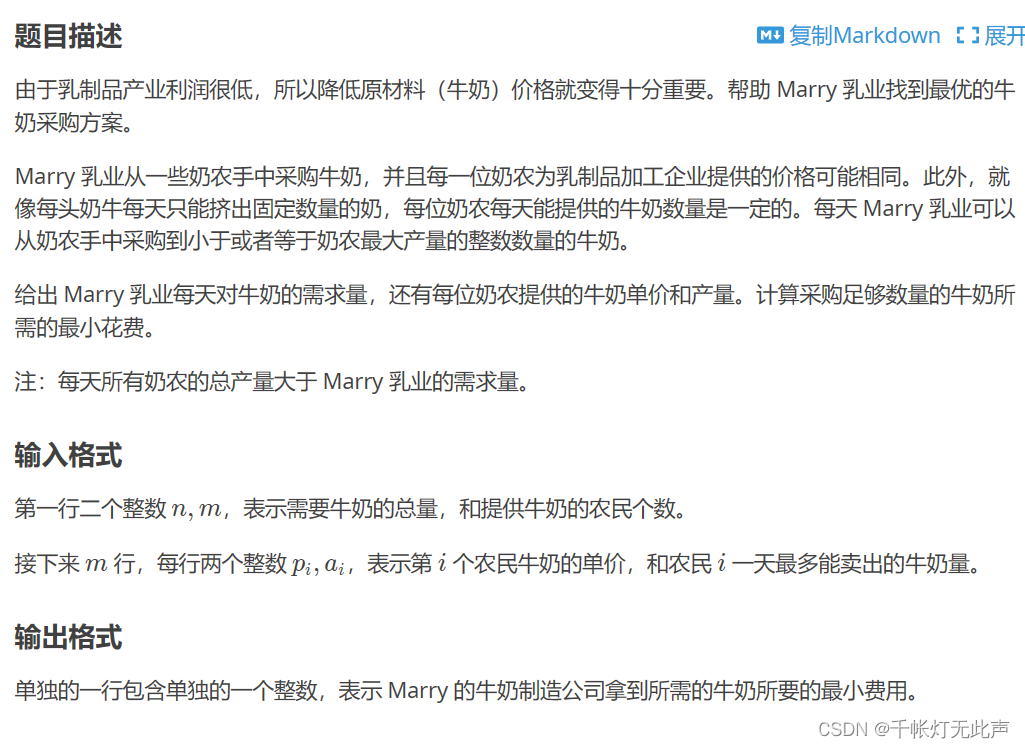
对单价升序排序后遍历

AC  代码

#include<iostream>
#include<algorithm> //sort()
using namespace std;
typedef long long LL;

struct milk
{
    LL price, all; //单价和产量
}a[5010];

bool cmp(milk x, milk y)
{
    return x.price < y.price;
}

int main()
{
    LL n, m, ans = 0; //剩余需要的数量n, 农民人数m, 最小费用ans
    cin>>n>>m;
    for(int i = 0; i < m; ++i)
        cin>>a[i].price>>a[i].all;
    sort(a, a + m, cmp); //单价升序排序
    //遍历不同单价的农民
    for(int i = 0; i < m; ++i) {
        if(n >= a[i].all) {
            ans += a[i].all * a[i].price;
            n -= a[i].all; //表示剩余需要的牛奶
        }
        else { //如果不需要那么多
            ans += n * a[i].price;
            n = 0;
        }
    }
    cout<<ans;

    return 0;
}

🌳P4995 跳跳！

P4995 跳跳！ - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

标签：普及/提高-，贪心，排序

升序排序后...

显然，先从地面跳到最高的石头，再从（未跳过的）最高的跳到（未跳过的）最矮的...

因为题目说了，每个石头只跳1次

采用i, j两个相向的游标即可实现

AC  代码

#include<iostream>
#include<algorithm> //sort()
using namespace std;
typedef long long LL;
LL a[310];

LL resume(LL x, LL y) //耗费体力值
{
    return (x - y) * (x - y); //保证 x >= y
}

int main()
{
    LL n, ans = 0;
    cin>>n;
    for(LL i = 1; i <= n; ++i) //1开始输入
        cin>>a[i];
    sort(a + 1, a + n + 1); //升序排序
    //遍历, 先++i, 再++j, 再... 直到i == j
    LL i = 0, j = n, num = 1;
    while(i != j) {
        ans += resume(a[j], a[i]);
        if(num % 2 == 1) i++;
        else j--;
        num++;
    }
    cout<<ans;

    return 0;
}

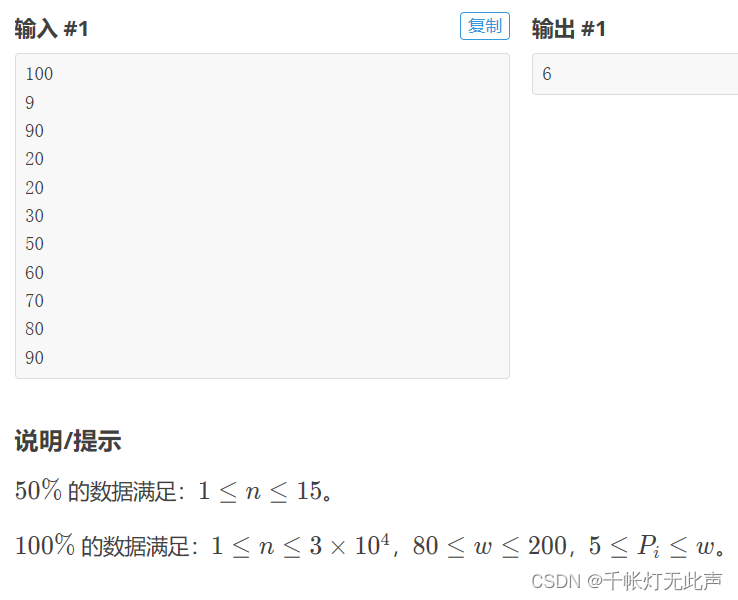
🌳P1094 [NOIP2007 普及组] 纪念品分组

P1094 [NOIP2007 普及组] 纪念品分组 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

标签：贪心，排序，普及-

（先升序排序）

这题和上题差不多，略微区别的是，两个游标的移动方式（都是相向移动）

上一题是i++ 和 j--轮着来

本题是先确定初始的 i，然后一直 j--，直到遇到第一个满足 a[i] + a[j] <= w的

把结果处理了，i++，继续j--，直到遇到下一个满足 a[i] + a[j] <= w...

额外测试

100
5
70
40
60
60
60
4

AC  代码

#include<iostream>
#include<algorithm> //sort()
using namespace std;
int a[30010];

int main()
{
    int n, w;
    cin>>w>>n;
    for(int i = 0; i < n; ++i)
        cin>>a[i];
    sort(a, a + n); //升序排序
    int i = 0, j = n - 1, ans = 0;
    while(i <= j) {
        while(a[i] + a[j] > w && i != j) {
            j--; //直到满足两件放一组的条件
            ans++; //1件纪念品占1组
        }
        j--;
        i++;
        ans++; //2件占1组, 当然最后一次i == j时1件占1组
    }
    cout<<ans;

    return 0;
}

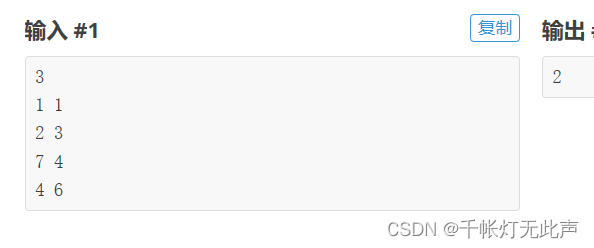
🌳P1199 [NOIP2010 普及组] 三国游戏

P1199 [NOIP2010 普及组] 三国游戏 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

标签：贪心，博弈论，普及//提高-

题目有点长，就不放了

思路

由于计算机自动选下一个和人配对最高的武将，（人先手）所以每一行最高的组合，人取不到，计算机也取不到，所以，人能必胜的条件，就是取到所有行第二高的组合中，的最大值

注意点补充

1，500*500 = 2.5 * 10^5，数据量达到1e5，用scanf()

2，对照下图去输入和排序，防止输入错误或者排序错误

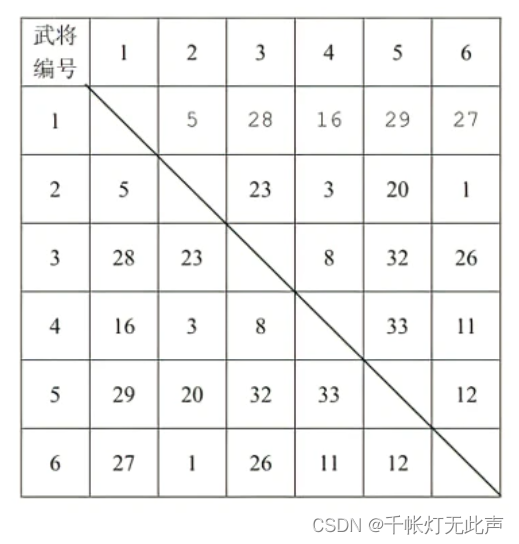
AC  代码

#include<iostream>
#include<cstdio> //scanf()
#include<algorithm> //sort()
using namespace std;
int a[510][510];

int main()
{
    int n, now = 0;
    scanf("%d", &n);
    for(int i = 1; i <= n - 1; ++i) //1~n-1
        for(int j = i + 1; j <= n; ++j) { //i+1 ~ n
            cin>>a[i][j];
            a[j][i] = a[i][j]; //无向, 对照草稿图, 输入完整
        }
    //人先选
    //最大都选不到, 人选最大的次大必胜, 不存在输的情况
    int ans = 0;
    for(int i = 1; i <= n; ++i) {
        sort(a[i] + 1, a[i] + 1 + n); //起点和终点地址
        ans = max(ans, a[i][n - 1]); //取次大最大值
    }
    cout<<1<<endl<<ans;

    return 0;
}

4
256032391 44492372 820892564
72613801 404834202
13297961
1
404834202

🌳P2672 [NOIP2015 普及组] 推销员

P2672 [NOIP2015 普及组] 推销员 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

标签：提高+/省选-，贪心，线段树，树状数组

本题在模拟清楚题意的基础上，借助贪心 + 前缀和 + 预处理，不用线段树，树状数组也能完成

好像只用贪心能解决

注意，下面的洛谷题解中，关于h[i]的描述不够严谨，不是后 i 个，而是第 i ~ 第 n 个

也就是第 i 到 最后一个住户（注意h[i]预处理是从n遍历到1的）

终点观察样例2

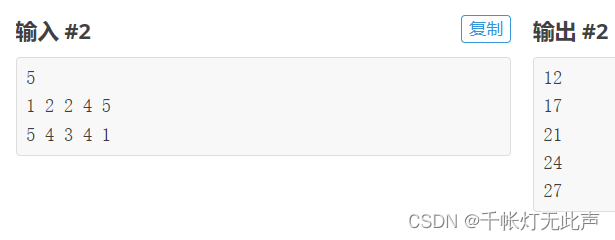
思路

只算一次最远路程，首先模拟一次样例2，结合链接的例子模拟一遍，

主要看它的例子

(71条消息) P2672 [NOIP2015 普及组] 推销员_c++ 推销员_smooth的博客-CSDN博客

 再看这个题解 P2672 【推销员】 - Rainy7の灯塔 - 洛谷博客 (luogu.com.cn)

蓝题对我来说太难了，我只是努力看懂题解，然后自己敲一遍

1，按疲劳值降序（大到小）排序       

2，sum(a[k])(1≤k≤X)+s[j]∗2

取前k个最大疲劳值的前缀和 + 前k个最大疲劳值中最大距离 * 2

3，推销员每走远一点，舍去前X大的最小值（即第X大），看能不能通过走更远来获取更大的疲劳值  （为什么只舍去一个呢，因为已经疲劳值大到小排序了，省略100字证明.........）

以上截图来自洛谷题解博客 👆

建议结合第一个链接的例子，来模拟这个过程，助于理解

核心思想： 只需舍去最小值来走更远，无需舍去更多数来走更远  

v[i].s表示距离，v[i].a表示疲劳值，q[i]表示前i个最大值，h[i]表示后i个最大值

sum[i]表示疲劳前缀和(不包含距离的因素，只是推销产品的疲劳值)

q[i]是前i个，在X和X之前的住户，所以

最后输出时，取max(sum[i] + q[i], sum[i - 1] + h[i]); 就应用了只舍去最小值的思想

sum[i] + q[i] 表示(前i个推销疲劳值的前缀和) + (前i个距离的最大值)（由题可知，只取距离最大值）

sum[i - 1] + h[i] (舍弃掉前X大中的最小值后)，+ (第i到最后一个 推销的疲劳值 和 最大距离的疲劳值)

拿第一个链接的数据举个例子（按疲劳值大到小排序后）

距离	4	1	3	5	2	6
疲劳值	5	4	3	3	2	1

当 X = 2，sum[i] + q[i] = (5 + 4) + (4 * 2)，注意q[i]只包含距离疲劳值

而 sum[i - 1] + h[i] = (5) + (6 * 2 + 1)，而h[i]包括距离疲劳值 + 销售疲劳值

 再放一次，多看看

数据范围不超过10^9，可以int

最后再解释下，有人有疑问，为什么h[i]可以直接sum[i - 1] + h[i]呢

万一最大值没有包含在前i个里呢

因为h[i]本身是从n开始遍历的，当它遍历到1时，已经包括了整个数组中疲劳值（距离+推销）的最大值

会有这个疑问的原因是，题解描述不够严谨，不应该说后i个，应该说第 i 到第n个

先模拟一遍过程，再想到直接暴力会TLE，然后用前缀和优化....题解看了很久很久很久

（看难题题解，没什么好办法，多模拟几遍，然后理解透了就自己敲一遍，对我来说确实难）

AC  代码

#include<iostream>
#include<cstdio> //scanf()
#include<algorithm> //sort()
using namespace std;
//sum[i]是推销的疲劳值的前缀和
//q[i]是前i个距离的疲劳值的最大值
//h[i]是第i到第n个 距离 + 推销的疲劳值最大值
int sum[100010], q[100010], h[100010];

struct node
{
    int s, a; //s表示距离distance, a表示推销的疲劳值
}v[100010];

bool cmp(node x, node y)
{
    return x.a > y.a; //推销的疲劳值大到小排序
}

int main()
{
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i)
        scanf("%d", &v[i].s); //读入距离
    for(int i = 1; i <= n; ++i)
        scanf("%d", &v[i].a); //读入推销的疲劳值
    sort(v + 1, v + 1 + n, cmp); //传入地址和比较函数
    //前缀和 + 预处理
    for(int i = 1; i <= n; ++i)
        sum[i] = sum[i - 1] + v[i].a; //推销疲劳值前缀和
    for(int i = 1; i <= n; ++i)
        q[i] = max(q[i - 1], 2*v[i].s); //前i个住户最大距离疲劳值预处理
    for(int i = n; i >= 1; --i)
        h[i] = max(h[i + 1], 2*v[i].s + v[i].a); //第i ~ n个住户总疲劳值预处理
    //输出
    for(int i = 1; i <= n; ++i)
        cout<<max(sum[i] + q[i], sum[i - 1] + h[i])<<endl;

    return 0;
}

🌳P1080 [NOIP2012 提高组] 国王游戏

P1080 [NOIP2012 提高组] 国王游戏 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

标签：普及+/提高，贪心，高精度，排序 

考虑到不会高精度，专门花了一天时间学习5种高精度👇

哎，本题难点不在于贪心，而在于处理高精度乘除法的输入输出

如果给定2个数确实好处理，但是多次输入就懵了

高精度_加减乘除（理论+模板+例题）_千帐灯无此声的博客-CSDN博客

思路

n = 10^4， a, b = 10^4，最大可达10^40000，长度达40000位的字符串，显然是高精度乘法

然后就是贪心：

首先看清楚题目：

1，左手上数字累乘的前提是，“排在该大臣前面的所有人”，不包括他自己

2，请看截图👇，需要注意的是，"a, b为整数，且 > 0"，整数这个点要注意

a. 贪心的实现

所以大臣1排在大臣2前面更优的条件是：

a1 * b1 < a2 * b2

最终按 a * b从小到大排序

（按这个思路，显然，最后一个大臣得到的金币最多，只算最后一个大臣即可）

b. 高精度的实现

乘法部分：高精 * 低精度（2层for循环）(乘法需要乘n - 1次)

除法部分：高精 / 低精度（逐位试商法）（除法只需最后除1次）

请看博客：高精度_加减乘除（理论+模板+例题）_千帐灯无此声的博客-CSDN博客

c. 如何读入

下标从1开始，具体为什么，请看博客👆中的“大整数乘法”

不看题解代码，了解思路后自己敲，速度真的很慢。。。而且最后还容易TLE

未  AC  代码 

这道题做到一半，阳了，没办法

基本思路全了，就差每一部分的debug，不想做了，放这先

至少，贪心的思路模拟了，高精度也入门了

#include<iostream>
#include<algorithm> //sort()
#include<cstdio> //scanf()
#include<cstring> //memset()
using namespace std;
//最多40000位数字
int a[40010], aa[20]; //a[]左手累乘结果, aa[]每个大臣左手金币数更新进去
int tmp[40010]; //高精度乘法的中间数组

struct node
{
    int l, r; //左手右手金币
}num[10010]; //num每个大臣左右手

bool cmp(node x, node y)
{
    return x.l*x.r <= y.l*y.r; //左手*右手, 小到大排序
}

//将单个低精度数字更新到数组里, 低位在前
void in(int *a, int x)
{
    for(int i = 1;; ++i) { //下标1开始
        if(!x) break; //x输入完毕
        a[i] = x % 10;
        x /= 10;
        a[0]++; //a[0]保存左手数字长度
    }
} //全局变量中a[0]表示累乘长度, aa[0]表示右手数字长度

void cpy(int *x, int *y) //数组x拷贝到数组y上
{
    for(int i = 0; i <= 40000; ++i)
        y[i] = x[i];
}

int main()
{
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n + 1; ++i) //下标1表示国王
        scanf("%d%d", &num[i].l, &num[i].r);
    sort(num + 2, num + n + 2, cmp); //国王不参与排序
    //先将国王左手数字存入a[]
    in(a, num[1].l);

    //遍历每个大臣左手
    for(int k = 2; k <= n; ++k) { //k == n就是第 n - 1个大臣
        in(aa, num[k].l); //低位开始存入数组aa[]
        //清空中间数组
        memset(tmp, 0, sizeof(tmp));

        //高精度乘法部分
        for(int i = 1; i <= a[0]; ++i)
            for(int j = 1; j <= aa[0]; ++j) {
                tmp[i + j - 1] += a[i] * aa[j]; //按位相乘
                //每次乘完后进位
                tmp[i + j] += tmp[i + j - 1] / 10;
                tmp[i + j - 1] %= 10; //保留个位
            }
        cpy(tmp, a); //tmp[]拷贝到a[]
        //更新a[]大小, 最大可达a[0] + aa[0]
        for(int i = a[0] + aa[0]; i >= 1; --i)
            if(a[i]) { //到达最高位
                a[0] = i; //得到当前数组大小
                break;
            }
    }

    //高精 / 低精: 逐位试商法
    //a[]就是被除数
    long long x = 0, b = num[n + 1].r; //x余数, b商
    for(int i = a[0]; i >= 1; --i) { //高位开始
        a[i] = (x * 10 + a[i]) / b; //商
        x = (x * 10 + a[i]) % b; //余数
    }
    //输出商, 即最后一个大臣的金币数
    int kk = a[0];
    for(int i = kk; i >= 1; --i)
        if(a[i]) break; //排除前导0
    for(int i = kk; i >= 1; --i)
        cout<<a[i];
    //补充输出0的情况
    if(kk == 0) cout<<0;

    return 0;
}

🏆总结

先立业，后成家，没有一定的经济能力，吃个饭都抠抠索索，旅个游都犹犹豫豫，活着就真的没意思，所以，何必在这种情况下拉着另一个人来受罪呢