基于短时傅里叶变换的同步压缩变换原理

新的短时傅里叶变换(STFT)被定义为

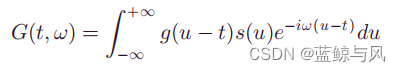
考虑一个单分量信号

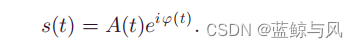
对相位$\phi (t)$进行泰勒展开，并丢弃二阶以及高阶项。

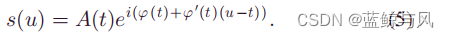
将上式带入STFT后，可得

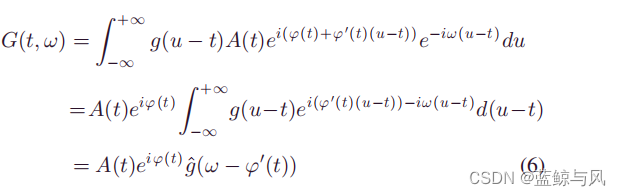
关于上式对时间$t$求导，得到关于瞬时频率${\phi }^{\prime }(t)$的表达式，

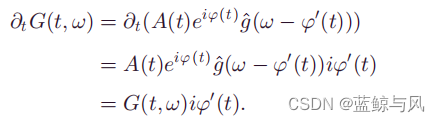
解出瞬时频率${\phi }^{\prime }(t)$，可得

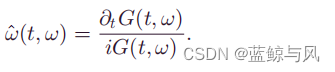
因此，把它作为瞬时频率估计式，定义同步压缩变换为

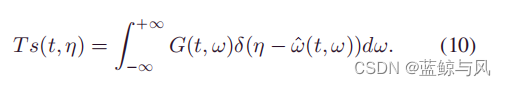
同步压缩变换以及大多数改进版本都是同样的套路，基于一个新的时频分析工具定义一个新的瞬时频率估计式，然后定义一个新的同步压缩变换。

Matlab代码

function [Ts] = SST(x,hlength);
% Computes the SST (Ts)  of the signal x.
% INPUT
%    x      :  Signal needed to be column vector.
%    hlength:  The hlength of window function.
% OUTPUT
%    Ts     :  The SST
%   Written by YuGang in Shandong University at 2016.5.13.
[xrow,xcol] = size(x);

if (xcol~=1),
 error('X must be column vector');
end; 

if (nargin < 1),
error('At least 1 parameter is required');
end;

if (nargin < 2),
hlength=round(xrow/5);
end;

Siglength=xrow;
hlength=hlength+1-rem(hlength,2);
ht = linspace(-0.5,0.5,hlength);ht=ht';

% Gaussian window
h = exp(-pi/0.32^2*ht.^2);
% derivative of window
dh = -2*pi/0.32^2*ht .* h; % g'

[hrow,hcol]=size(h); Lh=(hrow-1)/2; 

N=xrow;
t=1:xrow;

[trow,tcol] = size(t);


tfr1= zeros (N,tcol) ; 
tfr2= zeros (N,tcol) ; 

tfr= zeros (round(N/2),tcol) ; 
Ts= zeros (round(N/2),tcol) ; 

for icol=1:tcol,
ti= t(icol); tau=-min([round(N/2)-1,Lh,ti-1]):min([round(N/2)-1,Lh,xrow-ti]);
indices= rem(N+tau,N)+1; 
rSig = x(ti+tau,1);
%rSig = hilbert(real(rSig));
tfr1(indices,icol)=rSig.*conj(h(Lh+1+tau));
tfr2(indices,icol)=rSig.*conj(dh(Lh+1+tau));
end;

tfr1=fft(tfr1);
tfr2=fft(tfr2);

tfr1=tfr1(1:round(N/2),:);
tfr2=tfr2(1:round(N/2),:);

ft = 1:round(N/2);
bt = 1:N;

%%operator omega
nb = length(bt);
neta = length(ft);

va=N/hlength;
omega = zeros (round(N/2),tcol);

for b=1:nb
omega(:,b) = (ft-1)'+real(va*1i*tfr2(ft,b)/2/pi./tfr1(ft,b));
end 


omega=round(omega);

for b=1:nb%time
    % Reassignment step
    for eta=1:neta%frequency
        if abs(tfr1(eta,b))>0.0001%you can set much lower value than this.
            k = omega(eta,b);
            if k>=1 && k<=neta
                Ts(k,b) = Ts(k,b) + tfr1(eta,b);
            end
        end
    end
end
Ts=Ts/(xrow/2);
end

实验结果

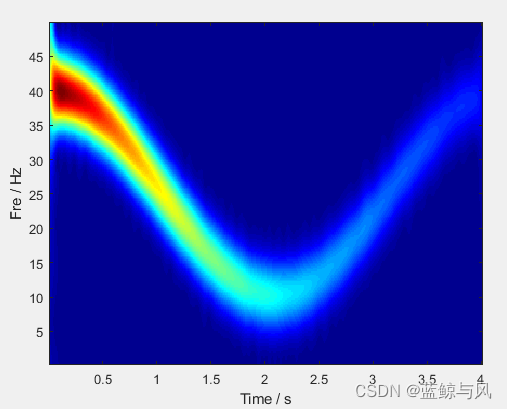
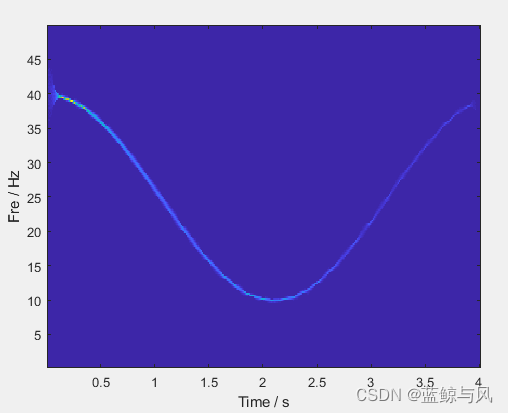
[1] Gang Y , Yu M , Xu C . Synchroextracting Transform[J]. IEEE Transactions on Industrial Electronics, 2017, 64(10):8042-8054.
[2] Yu G , Wang Z , Zhao P . Multisynchrosqueezing Transform[J]. Industrial Electronics, IEEE Transactions on, 2018.