- 东莞理工学院的同学可以借鉴,请勿抄袭
1.实验目的
通过实验达到:
-
理解和掌握树及二叉树的基本概念;
-
理解和掌握二叉树的顺序存储结构、链式存储结构;
-
理解和掌握采用二叉链式存储结构下二叉树的各种遍历操作的思想及 其应用;
-
加深对堆栈、队列的概念及其典型操作思想的理解;
-
掌握典型二叉树操作算法的算法分析。
2. 实验题目:二叉树的建立、遍历及其应用
设树结点的元素类型为 ElemType(可以为 char 或 int),采用二叉链(或三叉 链,即双亲孩子)存储,实现以下二叉树的各种基本操作的程序:
① 编写一个创建二叉树的函数,通过文件读取方式,建立不少于 10 个结点 的二叉树 T(建议用递归方式创建);
② 给定元素 x,在二叉树中查找该元素 x,若找到则返回该结点的指针;
③ 用凹入表示法打印该二叉树(可以是图 8-2 的形式或者 8.4.3 中的逆时针 旋转 90°,一个先序,一个中序 RDL);
④ 用非递归方式先序遍历方式输出树 T 的结点;(用到栈)
⑤ 用中序或后序遍历方式输出树 T 的结点;
⑥ 用层次遍历方式输出树 T 的结点;(用到队列)
⑦ 输出树 T 的深度;
⑧ 输出树 T 的叶子结点或非叶子结点;
⑨ 主函数设计菜单,通过菜单选择相应的函数调用实现以上各项操作。(在 实验报告中请画出测试的二叉树。) 附加题:(每完成一个额外附加 5 分,上限 10 分)
① 8-32 判断该二叉树是否为完全二叉树(层次遍历);
② 8-34 根据顺序存储建立二叉链存储的二叉树(与第 1 个操作类似);
③ 哈夫曼树编码问题的设计和实现(双亲孩子表示法+flag)。
一个表达式二叉树的例子: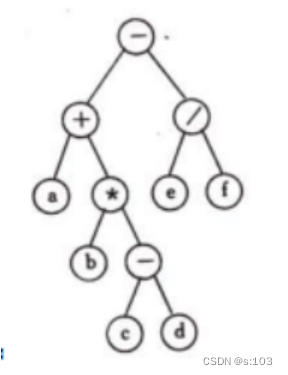
2.1. 数据结构设计
typedef char ElemType;
typedef struct Node {
ElemType value;
struct Node* left;
struct Node* right;
}Node;
2.2. 主要操作算法设计与分析
2.2.1. 读文件建立树函数
Node* createTreeByFile();
Node* createTreeByOrder(char string[]);
Node* createNode();
返回类型:Node*;
是否有参数:无
步骤:
- fopen打开文件读取字符串,此字符串是这种格式:“-+a##*b##-c##d##/e##f##”
- (麻烦老师说清楚点,我都不知道你是要我以层序遍历序列构造,还是以前中序或者后中序序列构造,还是以这种来构造…)
- 定义一个全局变量j记录字符串被读取到哪个下标
- 进入函数后,判断j下标是否为“#”,是则返回NULL,如果不是,调用createNode构造一个节点root
- 递归调用一次,将其赋值给root左孩子
- 再递归调用一次,将其赋值给root右孩子
- 返回root
算法时间复杂度:
- 时间复杂度为O(N);
- 空间复杂度为O(log2N);
2.2.2 返回x值对应节点的指针函数
Node* findNode(Node* root, ElemType value);
返回类型:Node*;
是否有参数:二叉树的根节点,键值x
步骤:
- root为NULL直接返回
- root对应值为x,返回root
- 递归调用左孩子,返回的值不为空则返回左孩子指针
- 递归调用右孩子,返回的值不为空则返回右孩子指针
- 否则返回空,没有找到
算法时间复杂度:
- 时间复杂度为O(N);
- 空间复杂度为O(log2N);
2.2.3. 凹入法打印二叉树函数
void incurvatePrint(char preorder[], char DRLorder[]);
buildTree(preorder, DRLorder);
Node* buildByIndex(char preorder[], char inorder[], int start, int end);
void print(Node* root, int n);
int search(char inorder[], int start, int end, char key);
返回类型:无返回值;
是否有参数:有,传入前序序列与DRL序列
步骤:
- incurvatePrint函数内调用buildTree函数获取二叉树,传入两个序列
- 调用buildByIndex函数获取二叉树,传入两个序列,以及0和strlen(inorder) - 1(from,to)
- 前序遍历序列的第一个值,就是根节点,在DRL中找到这个根节点下标,左边为右子树,右边为左子树,分别递归调用buildByIndex函数
- from > end 返回NULL
- 最终incurvatePrint调用print函数,传入root和0(n)用凹入法打印二叉树
- 每进入一层递归,传入的第二个参数都会加1
- 在打印root对应值之前,要递归函数,传入右孩子和n+1,之后要打印n个缩进,打印root值后打印回车符,调用递归函数,传入左孩子和n+1
算法时间复杂度:
- 时间复杂度为O(N2);
- 空间复杂度为O(log2N);
2.2.4. 非递归先序打印树函数
栈基本函数:
typedef struct Stack {
int size;
int capacity;
Node** arr;
}Stack;
Stack newStack() {
Node** arr = calloc(N, sizeof(Node*));
Stack stack = { 0, N, arr };
return stack;
}
void push(Stack* ps, Node* value) {
if (ps->size == ps->capacity) {
ps->arr = (Node**)realloc(ps->arr, 2 * ps->size * sizeof(Node*));
ps->capacity *= 2;
}
ps->arr[ps->size] = value;
(ps->size)++;
}
Node* pop(Stack* ps) {
if (ps->size == 0) {
printf("666,空了\n");
return NULL;
}
return ps->arr[--(ps->size)];
}
int isEmptyStack(Stack* ps) {
return ps->size == 0;
}
void preorderNormal(Node* root);
返回类型:无返回值;
是否有参数:有,传入二叉树根节点
步骤:
- 建立栈,打印根节点root,(为NULL则return)
- 定义cur为root的左孩子
- 进入循环,条件:栈不为空或者cur不为空
- 进入循环:如果左孩子不为空,压栈并打印节点对应值,cur=cur->left
- 循环停止cur赋值为栈弹出来的节点的右孩子
- 进入循环判断
- 结束循环,则打印结束
算法时间复杂度:
- 时间复杂度为O(N);
- 空间复杂度为O(log2N);
2.2.5. 中序遍历和后序遍历函数
void inorder(Node* root);
void postorder(Node* root);
无返回值,有参数,二叉树根节点
步骤:
- 根节点为NULL不打印
- 依次调用递归函数,传入左孩子和右孩子
- 中序遍历则是在两次调用之间,后序遍历则是两次调用之后
复杂度分析:
时间复杂度:O(N)
空间复杂度:O(logN)
2.2.6. 层序遍历函数
常用队列函数:
typedef struct Queue {
DataType* arr;
int size;
int capacity;
}Queue;
Queue createQueue() {
DataType* arr = (DataType*)calloc(N, sizeof(DataType));
Queue queue = { arr, 0, N };
return queue;
}
void offer(Queue* pq, DataType value) {
if (pq->size == pq->capacity) {
pq->arr = (DataType*)realloc(pq->arr, 2 * pq->size * sizeof(DataType));
pq->capacity *= 2;
}
pq->arr[pq->size] = value;
(pq->size)++;
}
DataType poll(Queue* pq) {
if (isEmptyQueue(pq)) {
printf("队列空\n");
exit(0);
}
DataType ret = pq->arr[0];
(pq->size)--;
memmove(pq->arr, pq->arr + 1, pq->size * sizeof(DataType));
return ret;
}
DataType peek(Queue* pq) {
if (isEmptyQueue(pq)) {
printf("队列空\n");
exit(0);
}
return pq->arr[0];
}
int isEmptyQueue(Queue* pq) {
return pq->size == 0;
}
void levelOrder(Node* root);
无返回值,传入参数为二叉树根节点
步骤:
- 根节点为NULL,则return
- 建立队列queue,根节点入队列
- 进入循环,条件:队列不为空
- Node* tmp接受出队列元素
- 打印tmp的值,将tmp的左孩子如队列,右孩子入队列(如果为NULL则不用)
- 直到出循环
复杂度分析:
时间复杂度:O(N)
空间复杂度:O(log2N)
2.2.7. 输出树的深度
int getHeight(Node* root);
返回int深度,传入二叉树根节点
步骤:
- root为NULL返回
- 调用两次递归函数,依次传入左孩子和右孩子
- 返回两个递归函数的返回值中的最大值加1
复杂度分析:
时间复杂度:O(N)
空间复杂度:O(log2N)
2.2.8. 输出树 T 的叶子结点或非叶子结点
void printLeafNode(Node* root);
void printNotLeaf(Node* root);
无返回值,传入二叉树根节点
步骤:
- root为NULL,return
- root不为NULL,
- printLeafNode函数如果root左右孩子都为NULL,则打印
- printNotLeaf函数中如果root左右孩子不全为NULL,则打印
- 调用两次递归函数,依次传入左孩子和右孩子
复杂度分析:
时间复杂度:O(N)
空间复杂度:O(log2N)
2.2.9. 判断该二叉树是否为完全二叉树
int isCompleteTree(Node* root)
返回int是与否,传入二叉树根节点
步骤:
- 如果root为NULL,返回1
- 定义队列queue,根节点入队列
- 进入循环,循环条件是queue不为空队列
- Node* cur接受出队列元素
- 如果cur不为NULL,左右孩子入队列
- 否则,一直出队列,如果队列中出现非NULL值,则返回0,否则返回1
- 若循环结束,返回1
复杂度分析:
时间复杂度:O(N)
空间复杂度:O(log2N)
2.2.10. 层序遍历序列构造二叉树(用2.2.9的类似操作)
Node* createTreeByLevelOrder(char string[]);
返回二叉树根节点,传入字符数组
步骤:
- 只要数组不为空,就先入队数组首元素,并用这个值创建二叉树的root。
- 然后进入循环,循环条件为队列不为空,取出队头元素,队头出队。
- 只要数组还有元素,就先给刚刚拿出的对头元素创建左孩子,然后左孩子入队。
- 同上,再创建右孩子,右孩子入队。
- 结束一次循环。回到2
复杂度分析:
时间复杂度:O(N)
空间复杂度:O(log2N)
2.2.11. main函数
int main() {
printf("===================================\n");
Node* root = createTreeByFile();
printf("===================================\n");
Node* XTree = findNode(root, '*');
printf("===================================\n");
printf("凹入法打印:\n");
incurvatePrint("-+a*b-cd/ef", "f/e-d-c*b+a");
printf("===================================");
printf("\n非递归前序:");
preorderNormal(root);
printf("\n递归前序:");
preorder(root);
printf("\nXTree前序:");
preorder(XTree);
printf("\n===================================");
printf("\n递归中序:");
inorder(root);
printf("\n递归后序:");
postorder(root);
printf("\n===================================");
printf("\n层序:");
levelOrder(root);
printf("\n===================================");
printf("\n深度:%d", getHeight(root));
printf("\n===================================");
printf("\n叶子节点:");
printLeafNode(root);
printf("\n非叶子节点:");
printNotLeaf(root);
printf("\n===================================\n");
printf("root%s完全二叉树", isCompleteTree(root) ? "是" : "不是");
printf("\n===================================\n");
levelOrder(createTreeByLevelOrder("123456789"));
}
2.3. 程序运行过程及结果
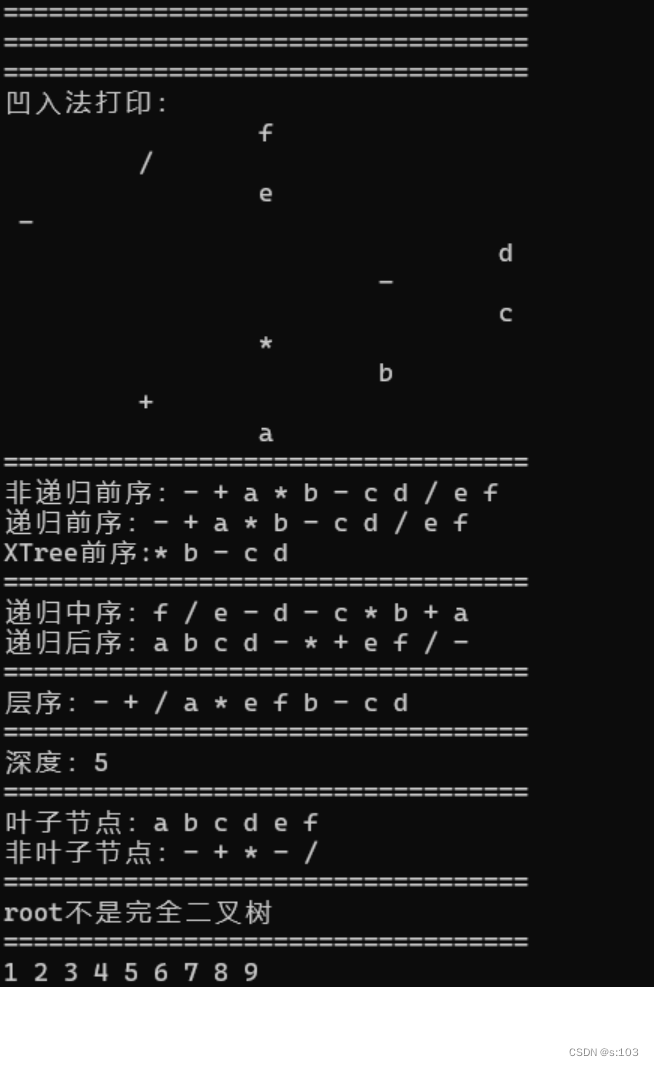
5. 总结
- 在这个过程中遇到很多问题,例如空指针异常,结果与预计结果不符
- 但是只要好好调试,总是能解决问题
- 对于递归的重点就是转化为子问题,整体性的思想
- 非递归实现则需要结合栈或者队列!
6. 附录:源代码
代码地址:码云连接