一、模拟退火算法（SA）

1.1 固体退火的原理

加热使得固体融化，然后缓慢地降低温度，以此来让固体内部的粒子排布更加均匀。

分为四个阶段：

升温阶段、降温阶段、等温阶段、达到目标温度退火完成

等温阶段就是在塑造形状。

1.2 Metropolis准则

概率接受新状态，称为Metropolis准则。

假设前一状态为 f(n)，系统受到一定扰动，状态变为 f(n+1)，相应地，系统能量由 f(n) 变为 f(n+1)。 定义系统由 f(n) 变为 f(n+1) 的接收概率为 p（probability of acceptance）：
$$p=\{\begin{array}{ll}1& \text{f(n+1) < f(n)}\\ e^{-\frac{f(n+1)-f(n)}{T}}& \text{f(n+1) >= f(n)}\end{array}$$

1.3 算法流程

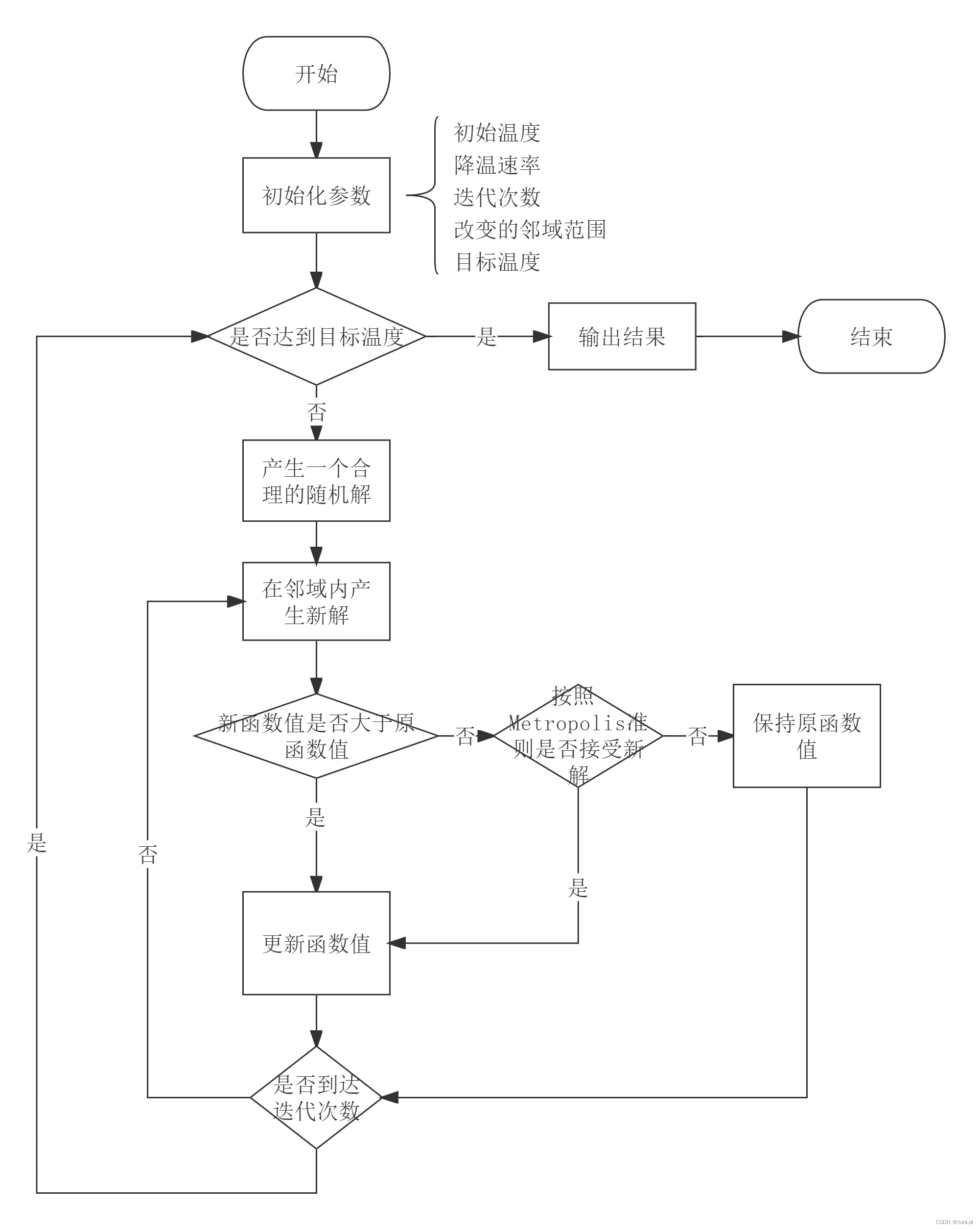
1.4 python代码求解f(x)的最小值点

1 示例求解的函数：

$$f(x)=\sqrt{|x|}+|x{|}^2$$

2 函数图像：

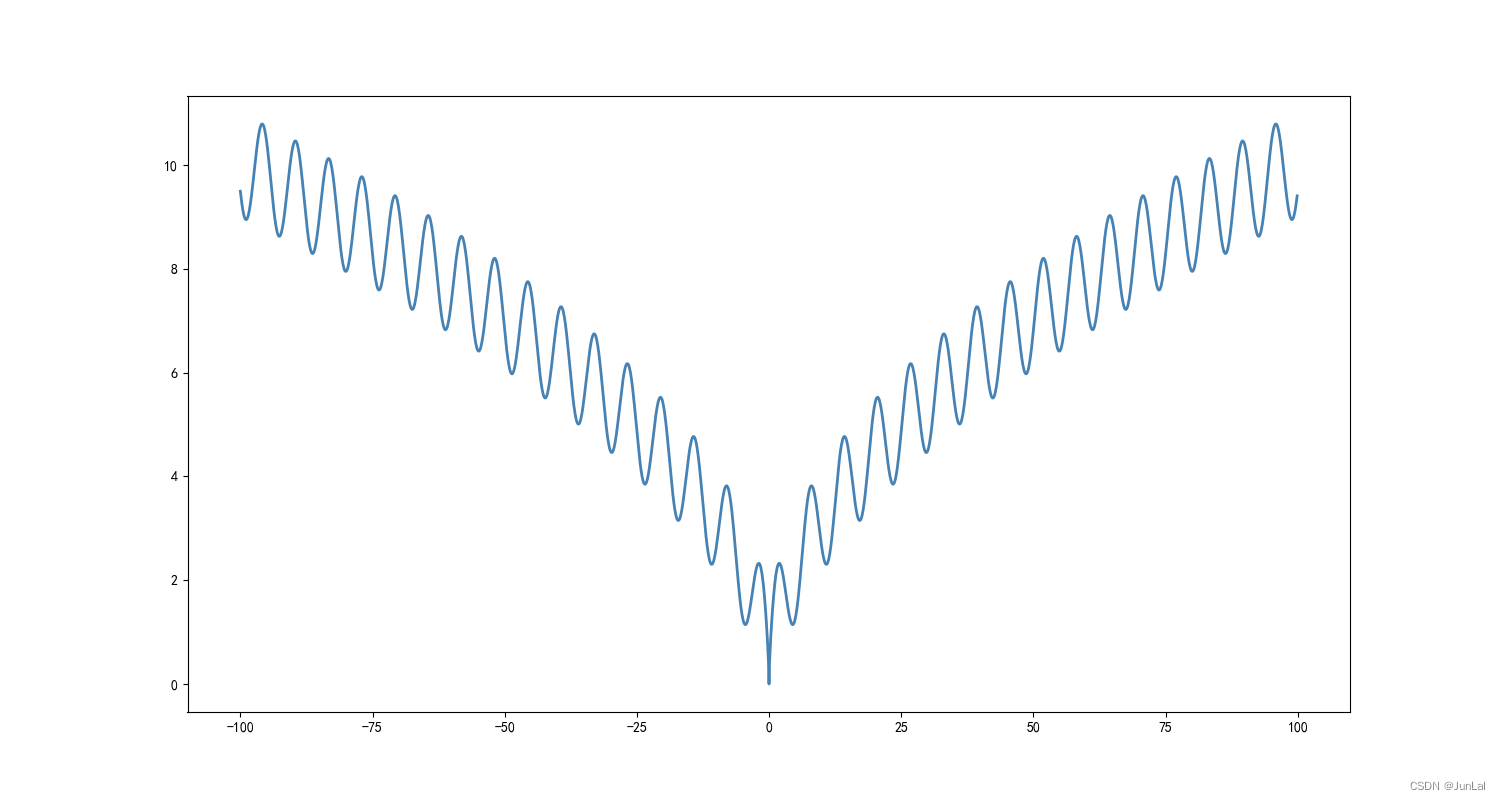
3 代码：

import math
import random
import numpy as np
import matplotlib.pyplot as plt

def cal_expression(x):
    return np.sqrt(np.absolute(x)) + np.sin(np.absolute(x))

def Metropolis(delta_f, T):
    if delta_f < 0:
        return True
    else:
        return True if np.exp(-(delta_f/T)) >= random.uniform(0, 1) else False

# 初始化
T = 100 # 初始温度
MAX_EPOCH = 200 # 迭代次数
LAMBDA = 0.99    # 退火速率
END_TEMP = 0.1  # 结束温度
CHANGE_NEIGHBORHOOD = 100 # 改变的邻域

# 存储结果
result = {}

while T > END_TEMP: # 未到达目标时
    # 随机一个解
    x = new_x = random.randint(-10000, 10000)
    y = cal_expression(x)
    for epoch in range(MAX_EPOCH):
        # 生成新的解
        new_x += random.uniform(-CHANGE_NEIGHBORHOOD, CHANGE_NEIGHBORHOOD)
        new_y = cal_expression(new_x)

        if Metropolis(new_y - y, T):
            x = new_x
            y = new_y
    # 记录当前温度的结果
    result[x] = y
    # 降温
    T *= LAMBDA

result_x, result_y = sorted(result.items(), key=lambda x:x[1])[0]
print("求解得到的最小值点为(", result_x, ",", result_y, ")")

# 图像绘图代码
def show_line_chart(data_x, data_y):
    # 这两行代码解决 plt 中文显示的问题
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus'] = False
    plt.figure(figsize=(15, 8))
    plt.plot(data_x,  # x轴数据
             data_y,  # y轴数据
             linestyle='-',  # 折线类型
             linewidth=2,  # 折线宽度
             color='steelblue',  # 折线颜色
             marker='o',  # 折线图中添加圆点
             markersize=6,  # 点的大小
             markeredgecolor='black',  # 点的边框色
             markerfacecolor='brown')  # 点的填充色
    plt.savefig("函数图像.png")
    plt.show()

# x = np.arange(-100, 100, 0.1)
# y = cal_expression(x)
# show_line_chart(x, y)

4 运行结果：