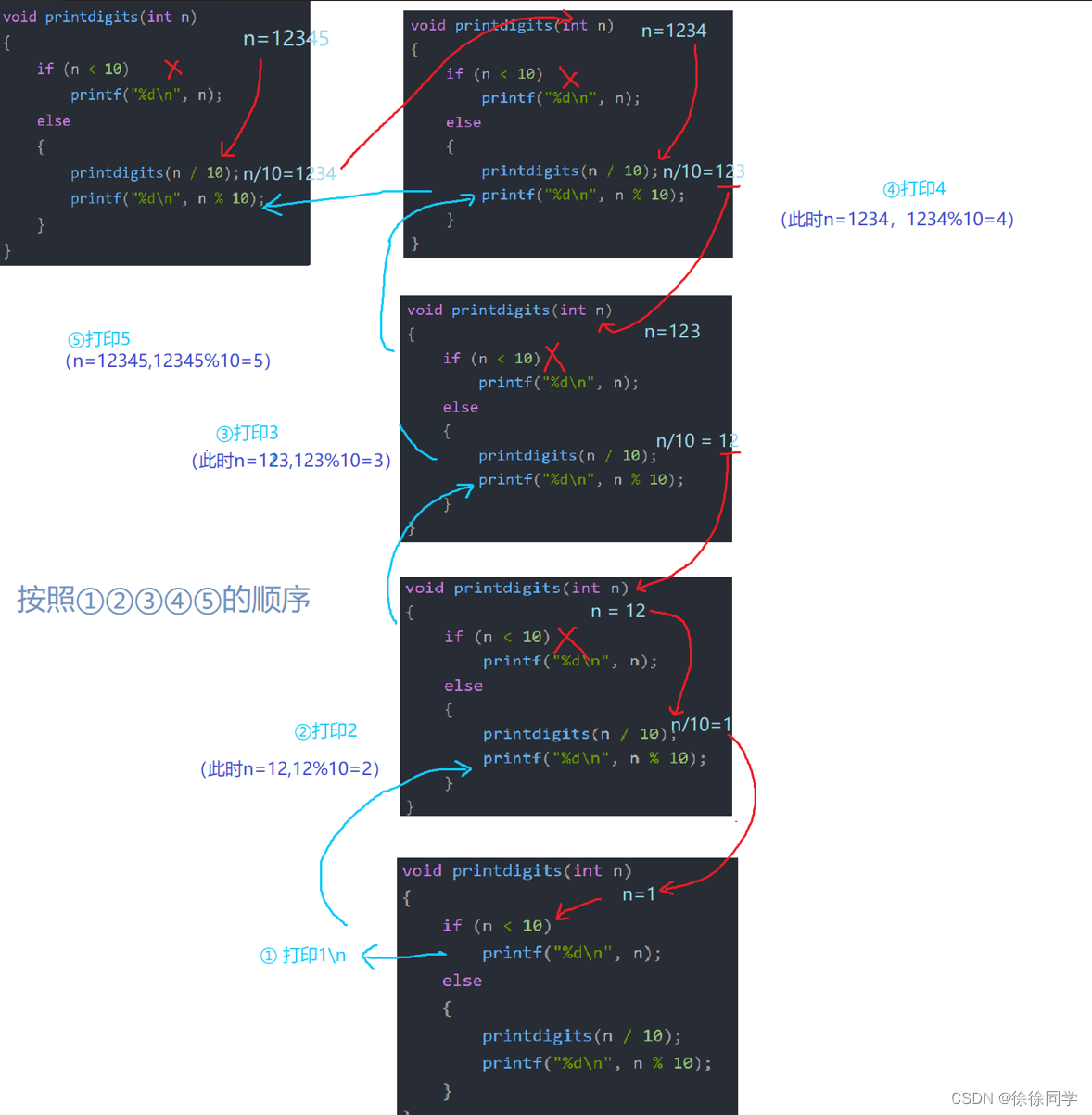
0动态规划

最优子结构&&最值问题&&重叠子问题 ---> 动态规划

引用别人的文章

1数字三角形

1.1题目

给定一个由 n行数字组成的数字三角形如下图所示。试设计一个算法，计算出从三角形
的顶至底的一条路径(每一步可沿左斜线向下或右斜线向下)，使该路径经过的数字总和最大。

输入格式:

输入有n+1行：

第 1 行是数字三角形的行数 n，1<=n<=100。

接下来 n行是数字三角形各行中的数字。所有数字在0..99 之间。

输出格式:

输出最大路径的值。

输入样例:

在这里给出一组输入。例如：
5 
7 
3 8 
8 1 0 
2 7 4 4
4 5 2 6 5 
输出样例:

在这里给出相应的输出。例如：
30

1.2代码

#include <bits/stdc++.h>
using namespace std;

int maxMatrix[101][101];

int main()
{
    int n;
    cin >> n;

    // 读入数据
    for (int i = 1; i <= n; ++i)
    {
        for (int j = 1; j <= i; ++j)
        {
            int temp;
            cin >> temp;
            maxMatrix[i][j] = temp;
        }
    }

    // 动态规划
    for (int i = 2; i <= n; ++i)
    {
        for (int j = 1; j <= i; ++j)
        {
            if (j == 1)
            {
                maxMatrix[i][j] += maxMatrix[i - 1][j];
            }
            else if (j == i)
            {
                maxMatrix[i][j] += maxMatrix[i - 1][j - 1];
            }
            else
            {
                maxMatrix[i][j] += maxMatrix[i - 1][j - 1] > maxMatrix[i - 1][j] ? maxMatrix[i - 1][j - 1] : maxMatrix[i - 1][j];
            }
        }
    }

    // 找出最大值
    int max = maxMatrix[n][1];
    for (int i = 2; i <= n; ++i)
    {
        if (maxMatrix[n][i] > max)
        {
            max = maxMatrix[n][i];
        }
    }

    cout << max;
    return 0;
}

1.3总结

最优子结构：通过n-1行数字三角形中每条路径的数字总和可以得出n行数字三角形中每条路径的数字总和。

最值问题：通过数字三角形中每条路径的数字总和，可以挑出数字总和最大的值。

重叠子问题：样例中以第5行第一个数和第5行第二个数为末尾的路径的数字总和的计算都会用到以第4行第一个数为末尾的路径的数字总和。

dp[i][j]二维数组：表示以第i行第j个数为末尾的路径的最大数字总和。

遍历顺序：遍历的终点是把第n行的所有数字全部遍历完。

代码思路：

数字三角形行数存入n中，数字三角形的元素值存入maxMatrix中，maxMatrix同时也表示dp二维数组。
正向遍历，如果第i行第j个数是本行第一个数，那么maxMatrix[i][j]就等于maxMatrix[i][j]+maxMatrix[i-1][j]；如果是本行最后一个数，那么maxMatrix[i][j]就等于maxMatrix[i][j]+maxMatrix[i-1][j-1]；否则，maxMatrix[i][j]等于maxMatrix[i][j]加上maxMatrix[i-1][j-1]和maxMatrix[i-1][j]中更大的数。
遍历第n行的maxMatrix，找出最大值。

2最长公共子序列

2.1题目

现在给你两个由AGCT四个字母构成的字符串，请你求出两个DNA序列的最长公共子序列。

输入格式:

两行，每行一个字符串，分别表示一个DNA序列（每个字符串长度不超过1000）。

输出格式:

一个数，最长公共子序列元素的个数。

输入样例:

在这里给出一组输入。例如：
AGCT
ATT
输出样例:

在这里给出相应的输出。例如：
2

2.2代码

#include <bits/stdc++.h>
using namespace std;
int maxLen[1001][1001];

int main()
{
    string s1, s2;
    cin >> s1 >> s2;

    for (int i = 1; i <= s1.length(); ++i)
    {
        for (int j = 1; j <= s2.length(); ++j)
        {
            if (s1[i] == s2[j])
            {
                maxLen[i][j] = maxLen[i - 1][j - 1] + 1;
            }
            else
            {
                maxLen[i][j] = maxLen[i - 1][j] > maxLen[i][j - 1] ? maxLen[i - 1][j] : maxLen[i][j - 1];
            }
        }
    }

    cout << maxLen[s1.length()][s2.length()];
    return 0;
}

2.3总结

最优子结构：通过s1[0-i]和s2[0-j]的最长公共子序列长度可以得出s1[0-(i+1)]和s2[0-(j+1)]的最长公共子序列长度。

最值问题：两个字符串的最长公共子序列就是dp[s1.length][s2.length]的值。

重叠子问题:dp[i][j]会在求dp[i+1][j+1]和dpdp[i+1][j]和dp[i][j+1]时用到。

dp[i][j]二维数据:表示s1[0~i]和s2[0~j]的最长公共子序列长度。

遍历顺序:遍历的终点是dp[s1.length][s2.length]。

代码思路：

s1和s2用来存储两个字符串,maxLen二维数组表示dp二维数组。
正向遍历,如果s1[i]==s2[j],那么maxLen[i][j]=maxLen[i-1][j-1]+1;否则,maxLen[i][j]=maxLen[i][j-1]和maxLen[i-1][j]的较大值。
maxLen[s1.length][s2.length]即为两个字符串的最长公共子序列长度。

注意：

公共子序列和公共子串：公共子序列可以不连续，公共子串必须连续。

3单调递增最长子序列

3.1题目

设计一个O(n2)时间的算法，找出由n个数组成的序列的最长单调递增子序列。

输入格式:

输入有两行：
第一行：n，代表要输入的数列的个数
第二行：n个数，数字之间用空格格开

输出格式:

最长单调递增子序列的长度

输入样例:

在这里给出一组输入。例如：
5
1 3 5 2 9
输出样例:

在这里给出相应的输出。例如：
4

3.2代码

#include <bits/stdc++.h>
using namespace std;
int main()
{
    int n;
    cin >> n;
    int array[100001];
    for (int i = 0; i < n; ++i)
    {
        cin >> array[i];
    }

    int maxLen[100001];
    for (int i = 0; i < n; ++i)
    {
        maxLen[i] = 1;
    }

    int max = maxLen[0];
    for (int i = 1; i < n; ++i)
    {
        for (int j = 0; j < i; ++j)
        {
            if (array[i] > array[j] && maxLen[i] >= maxLen[j])
            {
                maxLen[i] = maxLen[j] + 1;
                max = maxLen[i] > max ? maxLen[i] : max;
            }
        }
    }

    cout << max;
    return 0;
}

3.3总结

最优子结构：通过以第i个数结尾的单调递增子序列的长度可以得出以第j个数结尾的单调递增子序列的长度（j>i，第j个数是第一个比第i个数大的数）。

最值问题：比较n个最长单调递增子序列的长度，挑出最长的。

重叠子问题：第i个数结尾的单调递增子序列的长度会被多次用到。

dp[i]一维数组：用来表示以第i个数字结尾的最长单调递增子序列的长度。

遍历顺序：遍历的终点是把所有i遍历完。

代码思路：

n存入序列长度，array一维数组存放序列元素，maxLen一维数组表示dp数组，初始化为1（元素本身长度为1）。
max表示当前最长单调递增子序列长度。遍历这n个序列元素，对于每一个元素，都要遍历其前面的每一个元素，找出前面的小于自己的元素中最长单调子序列的长度，然后加1，赋给自己。
输出max。

4最大子段和

4.1题目

给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n]，求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时，定义子段和为0。

要求算法的时间复杂度为O(n)。

输入格式:

输入有两行：

第一行是n值（1<=n<=10000)；

第二行是n个整数。

输出格式:

输出最大子段和。

输入样例:

在这里给出一组输入。例如：
6
-2 11 -4 13 -5 -2
输出样例:

在这里给出相应的输出。例如：
20

4.2代码

#include <bits/stdc++.h>
using namespace std;

int n;
int maxSum[10001];

int main()
{
    cin >> n;
    int array[10001];
    int max = 0;
    for (int i = 1; i <= n; ++i)
    {
        cin >> array[i];
        maxSum[i] = array[i] + (maxSum[i - 1] > 0 ? maxSum[i - 1] : 0);
        max = maxSum[i] > max ? maxSum[i] : max;
    }

    cout << max;
    return 0;
}

4.3总结

最优子结构：通过以a[i]结尾的最大子段和可以得出以a[i+1]结尾的最大子段和。

最值问题：在所有的以a[i]结尾的最大子段和中找出最大值。

重叠子问题：求dp的过程中要用到，最终求最值也要用到。

dp[i]一维数组：表示以a[i]结尾的最大子段和。

遍历顺序：遍历的终点是把所有的以a[i]结尾的最大子段和都求出来。

代码思路：

n存储序列元素个数，array数组存储序列元素，maxSum表示dp。
正向遍历，如果maxSum[i]大于0，那么maxSum[i+1]=maxSum[i]+array[i]；否则，maxSum[i]=array[i]。max用来表示当前的最大子段和。
输出最大子段和。

5最大子矩阵和

5.1题目

最大子矩阵和问题。给定m行n列的整数矩阵A，求矩阵A的一个子矩阵，使其元素之和最大。

输入格式:

第一行输入矩阵行数m和列数n（1≤m≤100，1≤n≤100），再依次输入m×n个整数。

输出格式:

输出第一行为最大子矩阵各元素之和，第二行为子矩阵在整个矩阵中行序号范围与列序号范围。

输入样例1:
5 6
60 3 -65 -92 32 -70
-41 14 -38 54 2 29
69 88 54 -77 -46 -49
97 -32 44 29 60 64
49 -48 -96 59 -52 25
输出样例1:

输出第一行321表示子矩阵各元素之和，输出第二行2 4 1 6表示子矩阵的行序号从2到4，列序号从1到6
321
2 4 1 6

5.2代码

#include <bits/stdc++.h>
using namespace std;

int m, n;

int *getMaxSum(int *array)
{
    int dp[102][2] = {{0, 0}};
    int max = array[0];
    int begin = 1, end = 1;
    for (int i = 1; i <= n; ++i)
    {
        if (dp[i - 1][0] > 0)
        {
            dp[i][0] = dp[i - 1][0] + array[i - 1];
            dp[i][1] = dp[i - 1][1] + 1;
        }
        else
        {
            dp[i][0] = array[i - 1];
            dp[i][1] = 1;
        }
        if (dp[i][0] > max)
        {
            max = dp[i][0];
            end = i;
            begin = i - dp[i][1] + 1;
        }
    }

    // for (int i = 1; i <= n; ++i)
    // {
    //     cout << endl;
    //     cout << "dp[" << i << "][0] = " << dp[i][0] << " ";
    // }
    // cout << endl;

    int *result = new int[3];
    result[0] = max;
    result[1] = begin;
    result[2] = end;
    return result;
}

int *getResultArray(int array[][101], int hangShu)
{
    int *result = new int[102];
    for (int i = 0; i < n; ++i)
    {
        result[i] = 0;
    }

    for (int i = 0; i < hangShu; ++i)
    {
        for (int j = 0; j < n; ++j)
        {
            result[j] += array[i][j];
        }
    }

    return result;
}

int main()
{
    int matrix[101][101];
    cin >> m >> n;
    for (int i = 0; i < m; i++)
    {
        for (int j = 0; j < n; j++)
        {
            cin >> matrix[i][j];
        }
    }

    int *result = getMaxSum(matrix[0]);
    int max = result[0];
    int hangBegin = 1, hangEnd = 1, lieBegin = result[1], lieEnd = result[2];
    for (int i = 1; i <= m; ++i)
    {
        for (int j = 0; j <= m - i; ++j)
        {
            int *temp = getMaxSum(getResultArray(matrix + j, i));
            if (temp[0] > max)
            {
                // cout << "yes" << endl;
                max = temp[0];
                hangBegin = j + 1;
                hangEnd = hangBegin + i - 1;
                lieBegin = temp[1];
                lieEnd = temp[2];
            }
        }
    }

    cout << max << endl;
    cout << hangBegin << " " << hangEnd << " " << lieBegin << " " << lieEnd;
    return 0;
}