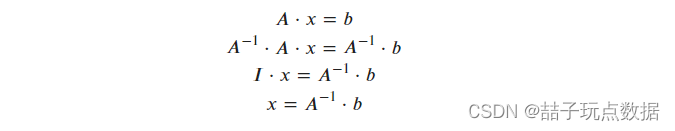香槟塔
难度:中等
我们把玻璃杯摆成金字塔的形状,其中第一层有 1 个玻璃杯,第二层有 2 个,依次类推到第 100 层,每个玻璃杯 (250ml) 将盛有香槟。
从顶层的第一个玻璃杯开始倾倒一些香槟,当顶层的杯子满了,任何溢出的香槟都会立刻等流量的流向左右两侧的玻璃杯。当左右两边的杯子也满了,就会等流量的流向它们左右两边的杯子,依次类推。(当最底层的玻璃杯满了,香槟会流到地板上)
例如,在倾倒一杯香槟后,最顶层的玻璃杯满了。倾倒了两杯香槟后,第二层的两个玻璃杯各自盛放一半的香槟。在倒三杯香槟后,第二层的香槟满了 - 此时总共有三个满的玻璃杯。在倒第四杯后,第三层中间的玻璃杯盛放了一半的香槟,他两边的玻璃杯各自盛放了四分之一的香槟,如下图所示。
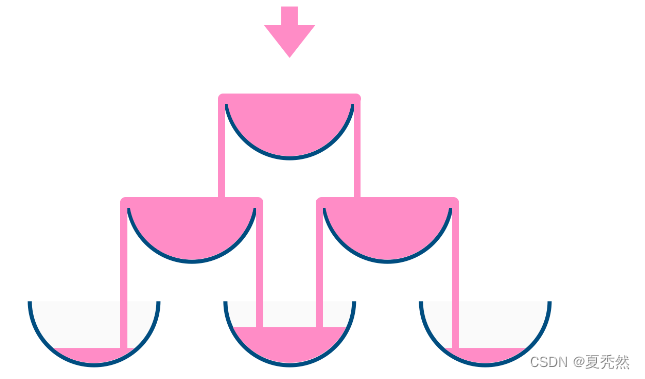
现在当倾倒了非负整数杯香槟后,返回第 i 行 j 个玻璃杯所盛放的香槟占玻璃杯容积的比例( i 和 j 都从0开始)。
示例 1:
输入: poured(倾倒香槟总杯数) = 1, query_glass(杯子的位置数) = 1, query_row(行数) = 1
输出: 0.00000
解释: 我们在顶层(下标是(0,0))倒了一杯香槟后,没有溢出,因此所有在顶层以下的玻璃杯都是空的。
示例 2:
输入: poured(倾倒香槟总杯数) = 2, query_glass(杯子的位置数) = 1, query_row(行数) = 1
输出: 0.50000
解释: 我们在顶层(下标是(0,0)倒了两杯香槟后,有一杯量的香槟将从顶层溢出,
位于(1,0)的玻璃杯和(1,1)的玻璃杯平分了这一杯香槟,所以每个玻璃杯有一半的香槟。
示例 3:
输入: poured = 100000009, query_row = 33, query_glass = 17
输出: 1.00000
模拟
思路:
可以模拟倒香槟过程。首先将所有的
poured
\textit{poured}
poured 杯香槟全部倒到
row
=
0
\textit{row} = 0
row=0 的这个杯子中。当有溢出时,再将溢出的部分平均倒到下一层的相邻的两个杯子中。而除了
row
=
0
\textit{row} = 0
row=0 的这个杯子中的香槟是直接来自于外部,其他杯子中的香槟均来自于它的上一层的相邻的一个或两个杯子中溢出的香槟。根据这个思路,可以求出每一层的每一只杯子中的香槟体积。求出
row
=
query_row
\textit{row} = \textit{query\_row}
row=query_row 的杯子的香槟体积后,取第
query_glass
\textit{query\_glass}
query_glass 个杯子中的体积,并与
1
1
1 求最小值返回。
时间复杂度:
O
(
q
u
e
r
y
_
r
o
w
2
)
O(query\_row^2)
O(query_row2)。使用了两层
for
\texttt{for}
for 循环。
空间复杂度:
O
(
q
u
e
r
y
_
r
o
w
)
O(query\_row)
O(query_row)。使用滚动数组实现的空间复杂度是
O
(
q
u
e
r
y
_
r
o
w
)
O(query\_row)
O(query_row)。
class Solution:
def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:
res = [poured]
for i in range(query_row):
next_row = [0] * (i+2)
for j, value in enumerate(res):
if value > 1:
more_value = (value-1)/2
next_row[j] += more_value
next_row[j+1] += more_value
res = next_row
return min(res[query_glass], 1)
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/champagne-tower




![[附源码]JAVA毕业设计衡师社团管理系统(系统+LW)](https://img-blog.csdnimg.cn/fbd924337d3e4b6bbbe68012bc231464.png)


![[附源码]JAVA毕业设计衡水特产展销系统(系统+LW)](https://img-blog.csdnimg.cn/4f51d9e7a1354178bfdd93af1e0eb15b.png)