目录
题目描述
思路分析
我的题解
题目描述
给你两个整数，被除数 dividend 和除数 divisor。将两数相除，要求 不使用 乘法、除法和取余运算。
整数除法应该向零截断，也就是截去（truncate）其小数部分。例如，8.345 将被截断为 8 ，-2.7335 将被截断至 -2 。
返回被除数 dividend 除以除数 divisor 得到的 商 。
注意：假设我们的环境只能存储 32 位 有符号整数，其数值范围是 [−231, 231 − 1] 。本题中，如果商 严格大于 231 − 1 ，则返回 231 − 1 ；如果商 严格小于 -231 ，则返回 -231 。
示例 1:
输入: dividend = 10, divisor = 3
输出: 3
解释: 10/3 = 3.33333.. ，向零截断后得到 3 。
示例 2:输入: dividend = 7, divisor = -3
输出: -2
解释: 7/-3 = -2.33333.. ，向零截断后得到 -2 。
提示：
-231 <= dividend, divisor <= 231 - 1
divisor != 0来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/divide-two-integers
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
思路分析
由于这题的数据是int型的，所以我们可以用二分的思路来解决（参考下面这篇博客）。
LeetCode_69. x 的平方根_小白麋鹿的博客-CSDN博客
https://yt030917.blog.csdn.net/article/details/129928642但这题并不这样做，这题主要是想介绍一下用位运算实现除法。
可以先了解如何用位运算实现乘法（参考下面这篇博客）
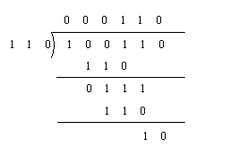
LeetCode_面试题 08.05. 递归乘法_小白麋鹿的博客-CSDN博客https://yt030917.blog.csdn.net/article/details/129918992那么思路都类似，就是模拟我们笔算的过程（参考下图）。首先定义一个初始值为ans的变量。每次让被除数左移或者除数右移，但为了防止右移过程中右移越界，一般选择让被除数左移。当移动到被除数恰好大于等于除数时（即再移动一位被除数就会小于除数的位置），记录此时右移的位数n，并将ans中对应的位置变成1（具体操作是ans或上1右移n位），并让被除数减去除数。然后循环往复，直至被除数小于除数为止。
但有一点需要特别注意的是，由于int型变量的数值范围是 [-2^31, 2^31 - 1] （不知道为什么的可以参考下面这段内容）
int型变量使用32位二进制数来表示，其中最高位是符号位，表示这个整数是正数还是负数。当符号位为0时，表示这个整数是正数，当符号位为1时，表示这个整数是负数。
因为最高位是符号位，所以int型变量的数值范围是由31位二进制数表示的数值范围决定。31位二进制数的最大值为2^31-1，也就是说，31位二进制数能够表示的最大正整数为2147483647。同样地，31位二进制数的最小值为负的2^31次方，也就是-2147483648。因此，int型变量的数值范围就是从-2147483648到2147483647。这就是为什么int型变量的数值范围是[-2^31, 2^31-1]。
所以我们还需要对变量值为INT_MIN的位置进行额外的讨论（这就使得程序显得有些冗杂，但却无法省去这一步）。代码书写见下方。
我的题解
//除法
int divide(int dividend, int divisor)
{
if (dividend == INT_MIN && divisor == INT_MIN)
return 1;
else if (divisor == INT_MIN)
return 0;
if (dividend == INT_MIN)
{
if (divisor == -1)
return INT_MAX;
else if (divisor == 1)
return INT_MIN;
//先让被除数+1，除以除数的结果tmp
//tmp与被除数的商再除以被除数的结果再加上tmp就是正确结果
int tmp = div(dividend + 1, divisor);
return tmp + div(dividend - multiply(tmp, divisor), divisor);
}
//以上部分均为处理INT_MIN的特殊情况
return div(dividend, divisor);
}
int div(int dividend, int divisor)
{
int tag = dividend ^ divisor;
dividend = dividend > 0 ? dividend : ~dividend + 1;
divisor = divisor > 0 ? divisor : ~divisor + 1;
int ans = 0;
while (dividend >= divisor)
{
int index = -1;
while (dividend >> ++index >= divisor);
index--;
dividend -= divisor << index;
ans |= 1 << index;
}
if (tag < 0)
ans = -ans;
return ans;
}
//乘法
int multiply(int A, int B)
{
int tag = A ^ B;
A = A < 0 ? -A : A;
B = B < 0 ? -B : B;
size_t product = sizeof(char[A][B]);
if (tag < 0)
product = -product;
return product;
}
