本期内容:栈,队列的定义性质,性质转换
栈,队列的定义性质,性质转换
- 认识栈
- 实现栈
- 队列
- 实现
- 性质转换
认识栈
栈(stack)又名堆栈,它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶,相对地,把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈,它是把新元素放到栈顶元素的上面,使之成为新的栈顶元素;从一个栈删除元素又称作出栈或退栈,它是把栈顶元素删除掉,使其相邻的元素成为新的栈顶元素。
就像是向水杯里放入乒乓球,然后逐一取出来。

栈因为本身的结构,所以接口实现时就只有数据的插入(栈顶),删除(栈顶),栈顶元素的获取。对于栈来说栈内的数据容易被遍历数据,遍历时就比较耗时。所以决定了栈就是先进后出FILO
实现栈
头文件包含:
typedef int STDataType;
typedef struct Stack
{
STDataType* _a;
int _top; // 栈顶
int _capacity; // 容量
}Stack;
// 初始化栈
void StackInit(Stack* ps);
// 入栈
void StackPush(Stack* ps, STDataType data);
// 出栈
void StackPop(Stack* ps);
// 获取栈顶元素
STDataType StackTop(Stack* ps);
// 获取栈中有效元素个数
int StackSize(Stack* ps);
// 检测栈是否为空,如果为空返回非零结果,如果不为空返回0
bool StackEmpty(Stack* ps);
// 销毁栈
void StackDestroy(Stack* ps);
实现:
#include"SL.h"
// 初始化栈
void StackInit(Stack* ps)
{
STDataType* new = (STDataType*)malloc(10*sizeof(STDataType));
if (new == NULL)
{
perror("malloc fail");
}
ps->_a = new;
ps->_capacity = 10;
ps->_top = 0;//相当于顺序表size。有效个数
}
// 销毁栈
void StackDestroy(Stack* ps)
{
assert(ps);
free(ps->_a);
ps->_a = NULL;
ps->_capacity = ps->_top = 0;
}
// 入栈
void StackPush(Stack* ps, STDataType data)
{
assert(ps);
if (ps->_top == ps->_capacity)
{
STDataType* tmp = (STDataType*)realloc(ps->_a, sizeof(STDataType) * 2 * ps->_capacity);
if (tmp == NULL)
{
perror("realloc fail");
}
ps->_a = tmp;
ps->_capacity *= 2;
}
ps->_a[ps->_top] = data;//数据入栈
ps->_top++;
}
// 出栈
void StackPop(Stack* ps)
{
assert(ps);
assert(ps->_top > 0);
ps->_a[ps->_top--];
/*ps->_top--;*/
}
// 获取栈顶元素
STDataType StackTop(Stack* ps)
{
assert(ps);
assert(ps->_top > 0);
return ps->_a[ps->_top - 1];
}
// 获取栈中有效元素个数
int StackSize(Stack* ps)
{
assert(ps);
return ps->_top;
}
// 检测栈是否为空,如果为空返回非零结果,如果不为空返回0
bool StackEmpty(Stack* ps)
{
assert(ps);
return ps->_top==0;
}
队列
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。
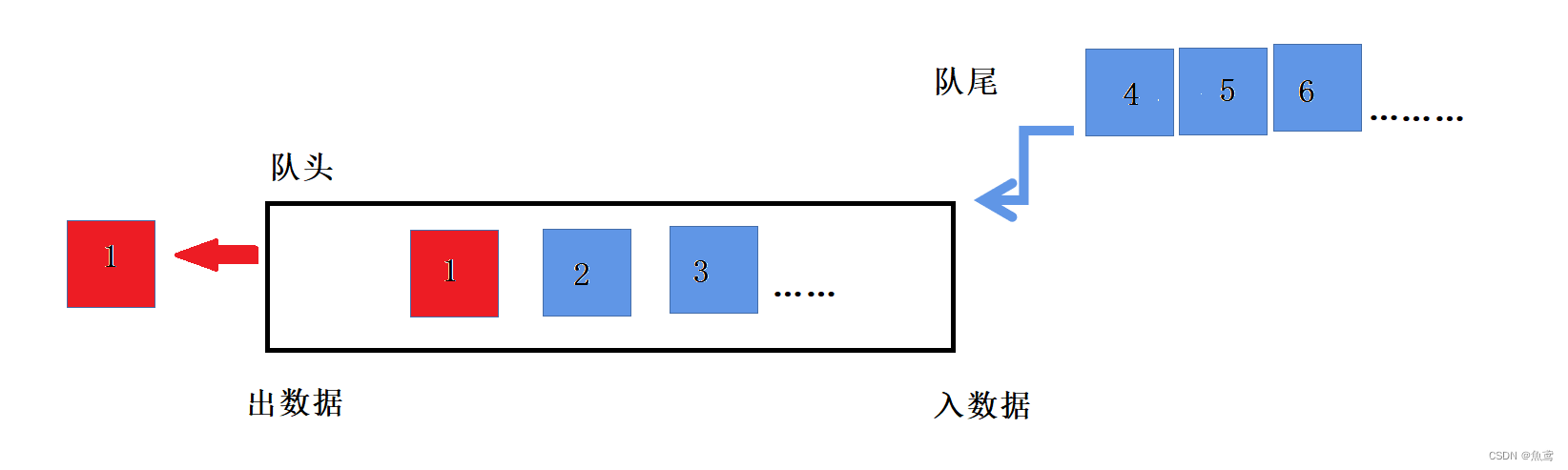
结构决定算法,所以队列就是先进先出FIFO。实现时选择链表结构实现。链表可以实现对于头部删除和尾部插入效率十分的高。数组实现需要挪动数据时间复杂度O(n)。
实现
// 初始化队列
void QueueInit(Queue* q)
{
assert(q);
q->size = 0;
q->_phead = NULL;
q->_tail = NULL;
}
// 队尾入队列
void QueuePush(Queue* q, QDataType data)
{
assert(q);
QNode* node = (QNode*)malloc(sizeof(QNode));
if (node == NULL)
{
perror("malloc fail");
}
node->_data = data;
node->_pNext = NULL;
if (q->_tail == NULL)
{
q->_phead=q->_tail = node;
}
else
{
q->_tail->_pNext = node;
q->_tail=node;
}
q->size++;
}
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
bool QueueEmpty(Queue* q)
{
assert(q);
return q->_phead && q->_tail;
}
// 队头出队列
void QueuePop(Queue* q)
{
assert(q);
assert(QueueEmpty(q));
if (q->_phead->_pNext == NULL)
{
free(q->_phead);
q->_phead = q->_tail = NULL;
}
else
{
QNode* del = q->_phead;
q->_phead = q->_phead->_pNext;
free(del);
}
q->size--;
}
// 获取队列头部元素
QDataType QueueFront(Queue* q)
{
assert(q);
return q->_phead->_data;
}
// 获取队列队尾元素
QDataType QueueBack(Queue* q)
{
assert(q);
return q->_tail->_data;
}
// 获取队列中有效元素个数
int QueueSize(Queue* q)
{
assert(q);
return q->size;
}
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);
QNode* cur = q->_phead;
while (cur)
{
QNode* del = cur;
cur = cur->_pNext;
free(del);
}
q->_phead = NULL;
q->_tail = NULL;
q->size = 0;
}
性质转换
用队列实现栈

思路:
对于使用队列的来说先进先出,栈是后进先出。这里实现时就是对于数据的输出顺序做调整。按照题目要求使用数定义栈,
1、push让一个队列不为空,一个队列始终为空。空队列用来存储push的值。不为空的用来模拟栈。
2、对于pop时有着一个队列没有pop空,这时就需要做一个假设,假设q1为空,q2不为空。判断假设是否正确,不正确就更换。
3、对于不为空的队列连续push前面n-1个数值到空队列中。不为空的队列最后一个就是栈顶元素。(比较灵活的一步)
代码参考;
typedef struct {
Queue Inqueue;
Queue Outqueue;
} MyStack;
MyStack* myStackCreate() {
MyStack* obj=(MyStack*)malloc(sizeof(MyStack));
QueueInit(&obj->Inqueue);
QueueInit(&obj->Outqueue);
return obj;
}
void myStackPush(MyStack* obj, int x) {
if(!QueueEmpty(&obj->Inqueue))
{
QueuePush(&obj->Inqueue,x);
}
else{
QueuePush(&obj->Outqueue,x);
}
}
int myStackPop(MyStack* obj) {
Queue* EmptyQ=&obj->Inqueue;
Queue* NoemptyQ=&obj->Outqueue;
if(!QueueEmpty(&obj->Inqueue))
{
EmptyQ=&obj->Outqueue;
NoemptyQ=&obj->Inqueue;
}
while(QueueSize(NoemptyQ)>1)
{
QueuePush(EmptyQ,QueueFront(NoemptyQ));
QueuePop(NoemptyQ);
}
int top=QueueFront(NoemptyQ);
QueuePop(NoemptyQ);
return top;
}
int myStackTop(MyStack* obj) {
if(!QueueEmpty(&obj->Inqueue))
{
return QueueBack(&obj->Inqueue);
}
else{
return QueueBack(&obj->Outqueue);
}
}
bool myStackEmpty(MyStack* obj) {
return (QueueEmpty(&obj->Inqueue)) && (QueueEmpty(&obj->Outqueue));
}
void myStackFree(MyStack* obj) {
QueueDestroy(&obj->Inqueue);
QueueDestroy(&obj->Outqueue);
free(obj);
}
栈实现队列

思路:
通过创建2个栈来对于数据进行数据倒序。需要确定栈的使用。push栈,pop栈需要明确,方便后面进行数据转换使用,
1、对于一个栈用来push,一个栈来使用pop。对于push栈来说始终对于数据插入,一个栈模拟出数据。
2、对于pop栈的栈顶元素,就是队列数据出栈。
typedef struct {
Stack ist;
Stack ost;
} MyQueue;
bool myQueueEmpty(MyQueue* obj);
MyQueue* myQueueCreate() {
MyQueue* obj=(MyQueue*)malloc(sizeof(MyQueue));
StackInit(&obj->ist);
StackInit(&obj->ost);
return obj;
}
void myQueuePush(MyQueue* obj, int x) {
assert(obj);
StackPush(&obj->ist,x);
}
int myQueuePop(MyQueue* obj) {
assert(obj);
assert(!myQueueEmpty(obj));
int top=myQueuePeek(obj);
StackPop(&obj->ost);
return top;
}
int myQueuePeek(MyQueue* obj) {
assert(obj);
assert(!myQueueEmpty(obj));
//倒数据
if(StackEmpty(&obj->ost))
{
while(!StackEmpty(&obj->ist))
{
StackPush(&obj->ost,StackTop(&obj->ist));
StackPop(&obj->ist);
}
}
return StackTop(&obj->ost);
}
bool myQueueEmpty(MyQueue* obj) {
assert(obj);
return StackEmpty(&obj->ist)&&StackEmpty(&obj->ost);
}
void myQueueFree(MyQueue* obj) {
assert(obj);
StackDestroy(&obj->ist);
StackDestroy(&obj->ost);
free(obj);
}
上面就是只栈与队列的基本性质定义,还有相互转换使用各自的特性实现。