📖 前言:人们常常说,“近朱者赤,近墨者黑“,”物以类聚,人以群分”,,我们想考察一个家庭的经济状况,可以问问住在哪里。如果家住在广州珠江新城,经济状况一定差不了,非富即贵。
在机器学习中,我们可以根据一个数据点(表示一个实体)周围其他数据点的类别情况,判断这个数据点的类别属性。因此引出我们今天讨论的内容——K近邻(K Nearest Neighbor, KNN)算法,在此基础上,进一步思考什么是好的模型。

目录
- 🕒 1. 什么是K近邻
- 🕘 1.1 分类的概念
- 🕘 1.2 K近邻分类
- 🕒 2. K值的选择
- 🕒 3. 距离的度量
- 🕘 3.1 欧式距离(L2距离或欧几里得距离)
- 🕘 3.2 余弦距离(Cosine Distance)
- 🕘 3.3 曼哈顿距离(L1距离或街区距离)
- 🕘 3.4 公式小结
- 🕒 4. 数据缩放
- 🕘 4.1 特征缩放
- 🕘 4.2 特征缩放的不同方法
- 🕘 4.3 特征缩放的语法
- 🕒 5. K近邻回归
- 🕒 6. K近邻模型
- 🕘 6.1 特点
- 🕘 6.2 语法
- 🕒 7. 监督学习中的误差来源
- 🕘 7.1 偏差与方差
- 🕤 7.1.1 偏差-方差权衡
- 🕒 8. 模型评价
- 🕘 8.1 已知推已知
- 🕘 8.2 已知推未知
- 🕤 8.2.1 语法
- 🕒 9. 交叉验证
- 🕘 9.1 语法
- 🕒 10. 综合案例——鸢尾花分类
- 🕒 11. 课后习题
🕒 1. 什么是K近邻
🕘 1.1 分类的概念
在介绍K近邻之前,先举个例子介绍分类的概念
一家花店想根据某顾客最近买花的情况,来预测某种新来的花是否会被该顾客购买
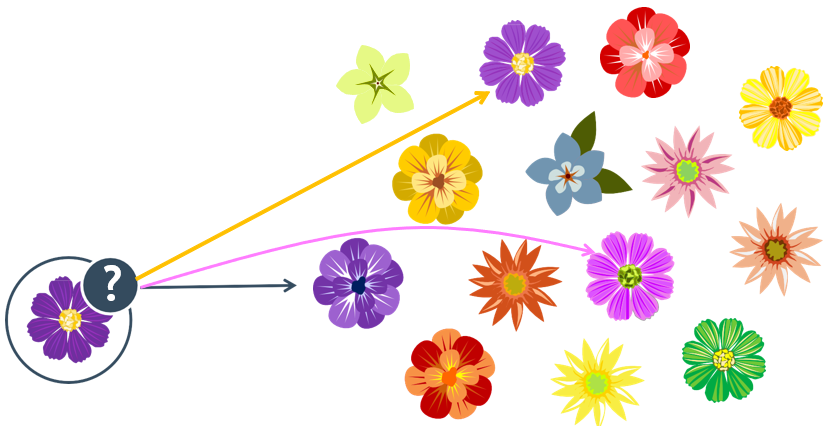
分类需要什么?
- 数据:
- 将对象表示为量化的一组特征
- 给定类别标签
- 对象间相似性的度量
🕘 1.2 K近邻分类
k近邻算法是一种基本分类和回归方法。即是给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的K个实例,这K个实例的多数属于某个类,就把该输入实例分类到这个类中。(这就类似于现实生活中少数服从多数的思想)
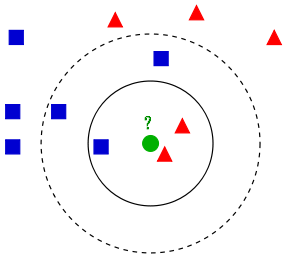
如上图所示,有两类不同的样本数据,分别用蓝色的小正方形和红色的小三角形表示,而图正中间的那个绿色的圆所标示的数据则是待分类的数据。接下来我们根据k近邻的思想来给这个绿色圆点进行分类。
- 如果K=3,绿色圆点的最邻近的3个点是2个红色小三角形和1个蓝色小正方形,少数从属于多数,基于统计的方法,判定绿色的这个待分类点属于红色的三角形一类。
- 如果K=5,绿色圆点的最邻近的5个邻居是2个红色三角形和3个蓝色的正方形,还是少数从属于多数,基于统计的方法,判定绿色的这个待分类点属于蓝色的正方形一类。
从上面例子我们可以看出,k近邻的算法思想非常的简单,原理即只要找到离它最近的k个实例,哪个类别最多即可。
那么,实际真的这么简单吗?其实,算法的核心思想确实是这样,但是要想一个算法在实际应用中被采纳,还有许多需要注意的地方,比如k怎么确定的,k为多少效果最好呢?所谓的最近邻又是如何来判断给定呢?接下来会一一讲解!
🕒 2. K值的选择
还是上面的例子,我们给它设定个极端情景(实际不可能存在,只做案例)
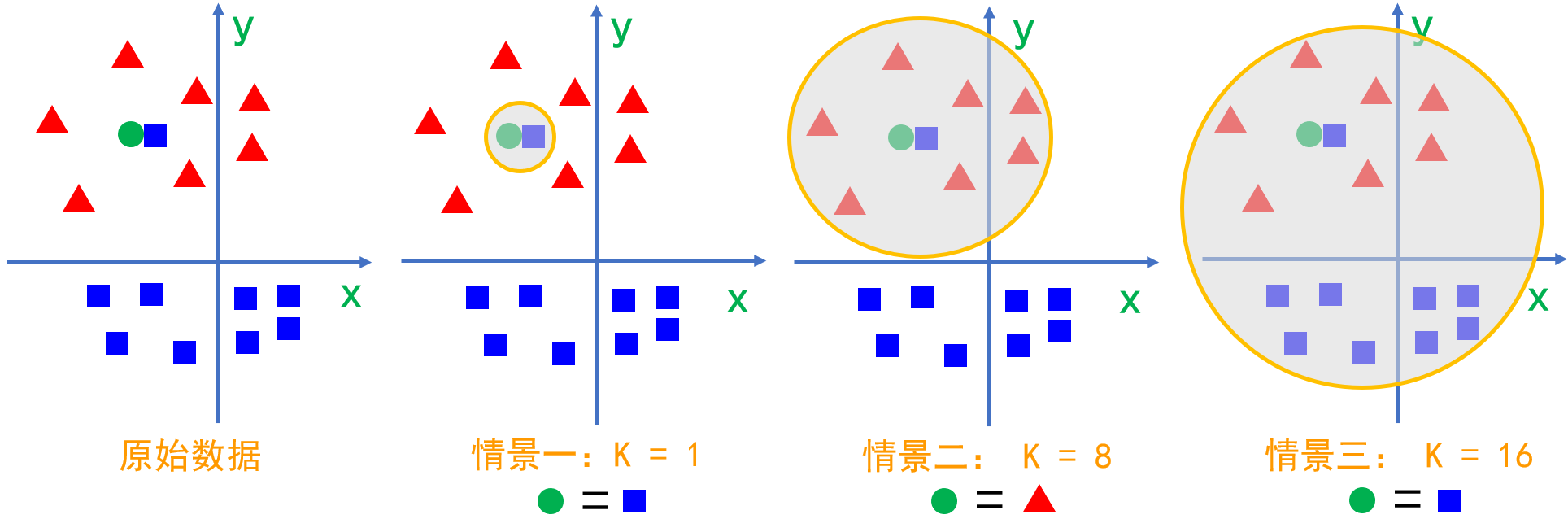
观察上图,可以得出以下结论:
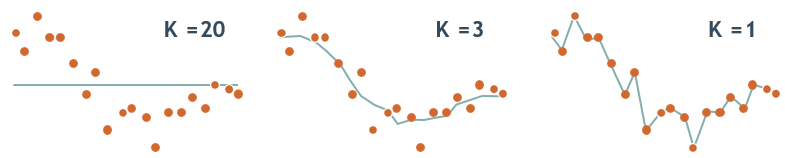
- k=1时,由于k值过小,待分类的数据容易学习到噪声,导致过拟合,使模型复杂化。
所谓的过拟合就是在训练集上准确率非常高,而在测试集上准确率低,经过上例,我们可以得到k太小会导致过拟合,很容易将一些噪声(如上图离绿点很近的蓝色正方形)学习到模型中,而忽略了数据真实的分布。
- k=8时,很容易得到正确的分类,即蓝色正方形。
- k=16(即全部训练样本)时,无论输入实例是什么,都将简单地预测它属于在训练实例中最多的类。与输入实例较远的(不相似)训练实例也会对预测起作用,使预测发生错误,k值的增大意味着整体模型变得简单。
小结:k值既不能过大,也不能过小,像上面k=8就是比较好的选择。此外,根据经验,一般来讲K值可以设定为训练样本数的平方根。
加权投票法
定义:是根据距离的远近,对近邻的投票进行加权,距离越近权重越大,权重为距离平方的倒数,最后确定当前数据点的类别。权重的计算公式为K个近邻的权重之和正好是1
W ( x , p i ) = e − D ( x , p i ) ∑ i = 1 k e − D ( x , p i ) W\left(x, p_{i}\right)=\frac{\mathrm{e}^{-D\left(x, p_{i}\right)}}{\sum_{i=1}^{k} \mathrm{e}^{-D\left(x, p_{i}\right)}} W(x,pi)=∑i=1ke−D(x,pi)e−D(x,pi)
那么一般会怎么选取呢?我们一般选取一个较小的数值,通常采取交叉验证法来选取最优的k值。(也就是说,选取k值很重要的关键是实验调参,类似于神经网络选取多少层这种,通过调整超参数来得到一个较好的结果)这些我们下期再介绍。
🕒 3. 距离的度量
在上面提到,k近邻算法是在训练数据集中找到与该实例最邻近的K个实例,这K个实例的多数属于某个类,我们就说预测点属于哪个类。
定义中所说的最邻近是如何度量呢?我们怎么知道谁跟测试点最邻近。这里就会引出我们几种度量俩个点之间距离的标准。
我们可以有以下几种度量方式:
🕘 3.1 欧式距离(L2距离或欧几里得距离)
对于两个数据点之间的相似度,可以用一个距离函数来表达。
可用的距离包括欧式距离、夹角余弦等
其中欧氏距离(Euclidean Distance)就是我们从初中开始就学的两点间距离公式
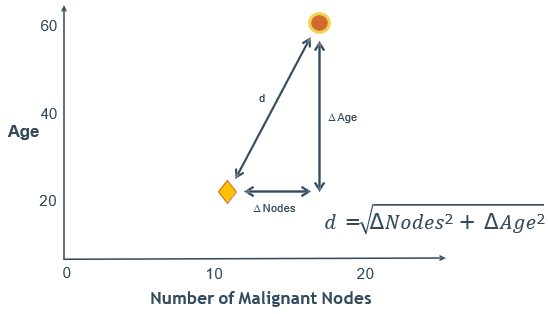
🕘 3.2 余弦距离(Cosine Distance)
如果要对文本进行分类,用夹角余弦计算距离(相似度)比欧式距离更为合适。
文本相似度计算的处理流程是:
(1)找出两篇文章的关键词;
(2)每篇文章各取出若干个关键词,合并成一个集合,计算每篇文章对于这个集合中的词的词频
(3)生成两篇文章各自的词频向量;
(4)计算两个向量的余弦相似度,值越大就表示越相似
距离越小,两个数据点属于同一类别的可能性越大。下面为距离公式( x x x为待分类的数据点(向量), p p p为近邻数据点)。
D ( x , p ) = { ( x − p ) 2 2 , 欧式距离 x ⋅ p ∣ x ∣ ⋅ ∣ p ∣ , 向量夹角余弦 D(x, p)=\left\{\begin{array}{l} \sqrt[2]{(x-p)^{2}}, \text { 欧式距离 } \\ \frac{x \cdot p}{|x| \cdot|p|}, \text { 向量夹角余弦 } \end{array}\right. D(x,p)={2(x−p)2, 欧式距离 ∣x∣⋅∣p∣x⋅p, 向量夹角余弦
🕘 3.3 曼哈顿距离(L1距离或街区距离)
在曼哈顿街区要从一个十字路口开车到另外一个十字路口,开车的距离肯定不可能是两点之间的直线距离,这个实际的开车距离就是曼哈顿距离(Manhattan Distance)。
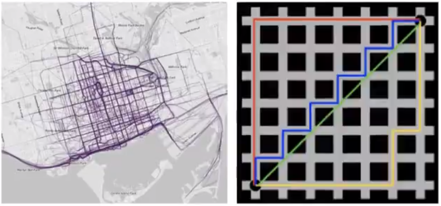
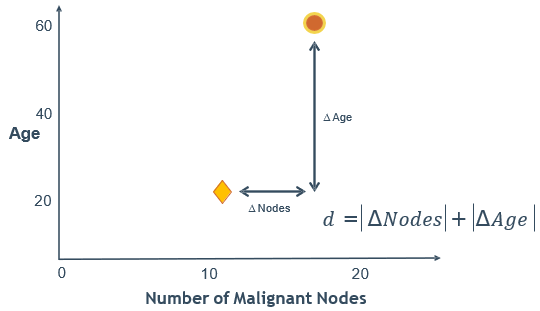
🕘 3.4 公式小结
二维平面上点a(x1,y1)和b(x2,y2)之间的欧式距离:
d
12
=
(
x
1
−
x
2
)
2
+
(
y
1
−
y
2
)
2
d_{12}=\sqrt{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}}
d12=(x1−x2)2+(y1−y2)2
夹角余弦距离:
cos
=
x
1
x
2
+
y
1
y
2
x
1
2
+
y
1
2
⋅
x
2
2
+
y
2
2
\cos =\frac{x_{1} x_{2}+y_{1} y_{2}}{\sqrt{x_{1}^{2}+y_{1}^{2}} \cdot \sqrt{x_{2}^{2}+y_{2}^{2}}}
cos=x12+y12⋅x22+y22x1x2+y1y2
曼哈顿距离:
d
12
=
∣
x
1
−
x
2
∣
+
∣
y
1
−
y
2
∣
d_{12}=\left|x_{1}-x_{2}\right|+\left|y_{1}-y_{2}\right|
d12=∣x1−x2∣+∣y1−y2∣
还有其他距离如汉明距离(Hamming Distance)、杰卡德距离(Jaccard Distance)、马氏距离(Mahalanobis Distance),有兴趣的同学可以去了解下。
🕒 4. 数据缩放
一般使用欧式距离来度量两个实体的相似度。我们从各个方面描述实体,也就是说,实体具有一系列的特征(属性),如果其中一个特征,其取值很大,比如取值在[80,100],而其他的特征取值都很小,比如取值范围为〔0,1],那么根据欧式距离公式,整个距离将被取值范围较大的那个特征所主导。为了避免此类情况发生,一般对各个属性进行缩放,比如都缩放到[0,1],以便每个特征属性对距离有大致相同的贡献。
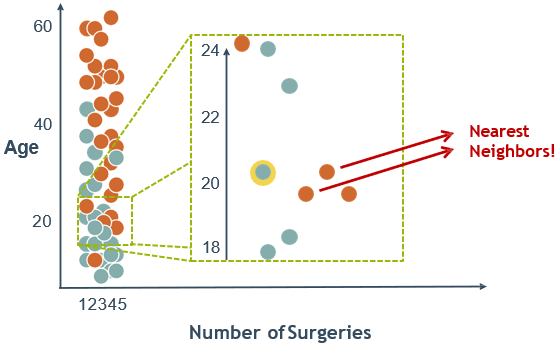
Age特征值跨度相对过大,成为决定样本距离的关键因素。
🕘 4.1 特征缩放
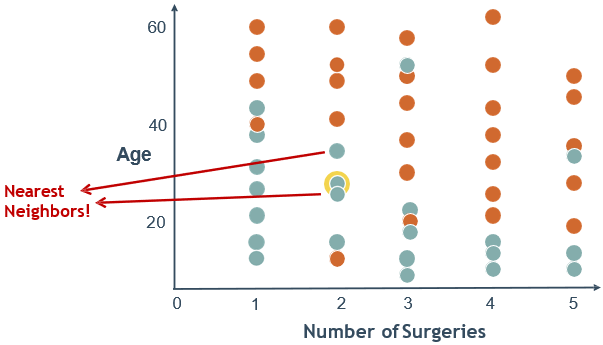
🕘 4.2 特征缩放的不同方法
Standard Scaler:即标准化,尽量将数据转化为均值为0,方差为1的数据( x ∗ = x − μ σ \mathrm{x}^{*}=\frac{x-\mu}{\sigma} x∗=σx−μ ),形如标准正态分布(高斯分布)。Minimum-Maximum Scaler:将数据缩放到某一给定范围(通常是[0, 1])。Maximum Absolute Value Scaler:通过除以最大绝对值,将数据缩放到[-1, 1]。
使各特征的数值都处于同一数量级上。
StandardScaler:数据预处理。针对每一个特征维度,去均值和方差归一化。关于归一化:
1)归一化后加快了梯度下降求最优解的速度,避免无法收敛;
2)归一化有可能提高精度,避免某些特征值域范围过大主导距离计算;
3)概率模型(如决策树等)不需要归一化;
4)需计算样本距离的一般需归一化。
5)举个例子:有个鞋码的数据集,需要根据鞋码预测是男鞋还是女鞋
🕘 4.3 特征缩放的语法
导入包含缩放方法的类:
from sklearn.preprocessing import StandardScaler
创建该类的一个对象(以标准化为例):
StdSc = StandardScaler()
拟合缩放的参数,然后对数据做转换:
StdSc = StdSc.fit(X_data)
X_scaled = StdSc.transform(X_data)
# 或者
X_scaled = StdSc.fit_transform(X_data)
🕒 5. K近邻回归
回归,预测f(x):与k近邻分类原理类似,f(x)取x的k个近邻的f平均值。
🕒 6. K近邻模型
🕘 6.1 特点
- 建模快(lazy-learning),因为它只是简单地存储数据
- 运行速度慢,因为需要计算很多的距离
- 占用内存多,如果数据集大的话
🕘 6.2 语法
导入包含分类方法的类:
from sklearn.neighbors import KNeighborsClassifier
创建该类的一个对象:
KNN = KNeighborsClassifier(n_neighbors=3)
拟合数据集,即训练KNN模型,并用训练好的模型预测数据的标签:
KNN = KNN.fit(X_data, y_data)
y_predict = KNN.predict(X_data)
这种 fit 和 predict/transform 语法会贯穿整个课程
回归使用KNeighborsRegressor
- n_neighbors是近邻节点的数量,也就是在判断本数据点的类别属性时,需要参考多少个近邻数据点。缺省值是5,用户可以根据需要进行设定。
- weights表示本数据点与近邻数据点的距离权重如何设定。可以使用的值主要有“uniform”和“distance”,表示采用均匀的权重或者根据距离赋予权重,也就是距离越近的数据点权重越大,距离越远的数据点权重越小等。
更多参数参考:🔎 Scikit-learn KNN分类器在线文档
🕒 7. 监督学习中的误差来源
Error = Bias 2 + Variance + Noise \color{blue}\textbf{Error = Bias}^{2}\textbf{ + Variance + Noise} Error = Bias2 + Variance + Noise
偏差和方差是针对模型的一般化或者泛化(generalization)而言的。在机器学习中,用数据集去训练一个模型,通常是定义一个损失函数(loss function),来衡量模型在这个数据集上预测的误差(或者损失),然后通过将这个误差最小化来学习一个恰当的模型。学习一个模型的目的是为了解决实际问题(或者说这个领域中的一般化问题),单纯将训练误差最小化,并不能保证在解决更一般的问题(即预测未知数据)时模型仍然是最优的,甚至不能保证模型是可用的。模型在这个训练数据集上的损失与一般化数据集上的损失之间的差异就叫做泛化误差(generalization error),泛化误差可细分为偏差和方差两部分。
🕘 7.1 偏差与方差
如果能获得有关一个问题的所有可能的数据,并在这个数据集上将损失最小化,这样训练得到的模型就可称为真实模型。然而,获得并训练所有可能的数据是不现实的,所以真实模型无法获得,我们的最终目标就是去学习一个模型使其尽可能接近这个真实模型。偏差和方差分别从两个方面描述了学习到的模型与真实模型之间的差距。
- 偏差(Bias):模型的期望输出值(即用不同数据集训练出的所有模型输出的平均值)与真实值之间的差异。即学习算法的期望预测与真实结果的偏离程度,刻画了学习算法本身的拟合能力。
- 方差(Variance):用不同数据集训练出的模型的输出值之间的差异。即数据的变动所导致的学习性能的变化,刻画了学习算法的稳定性。
假设模型M是一个射击学习者,训练数据集D,D.,…,D、就是N个独立的训练计划。
如果一个学习者是正常人,另一个学习者眼睛斜视,则斜视者无论参加多少训练计划,都不会打中靶心,问题不在训练计划够不够好,而在他的先天缺陷。这就是模型偏差产生的原因,学习能力不够。正常人参加N个训练计划后,虽然也不能保证打中靶心,但随着N的增大,会越来越接近靶心。
假设还有一个超级学习者,他的学习能力特别强,参加训练计划D时,他不仅学会了瞄准靶心,还敏锐地捕捉到了训练时的风速和光线,并据此调整了瞄准的方向,此时,他的训练成绩会很好。但是,他在参加测试时的光线和风速肯定与他训练时的不一样,他仍然按照训练时的瞄准方法去打靶,肯定打不好。这样产生的误差就是方差。这就是聪明反被聪明误。
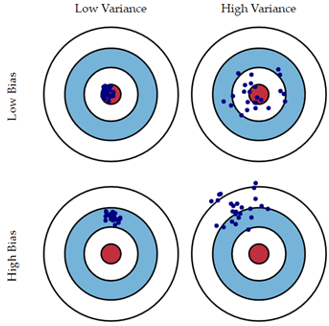
总结一下:学习能力不行造成的误差是偏差(欠拟合),学习能力太强造成的误差是方差(过拟合)。所以,最好的模型就是学习能力刚刚好的射手,既能够学习到瞄准的基本办法,又不会画蛇添足地学习太多细枝末节。
🕤 7.1.1 偏差-方差权衡
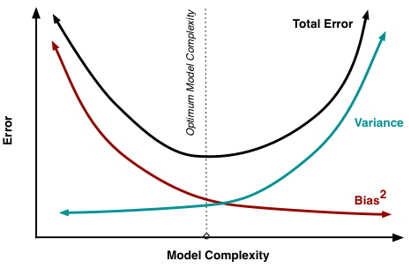
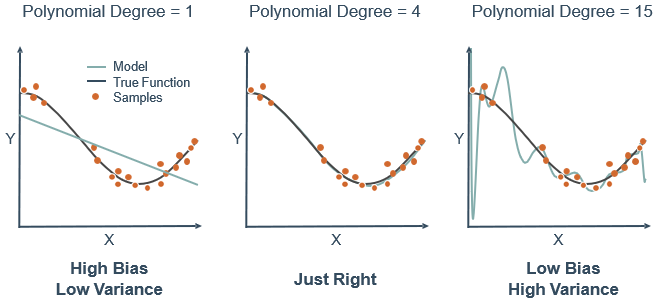
模型复杂度与偏差和方差的关系如下图所示。当模型过于简单时,学习器的拟合能力不够强,训练数据的扰动不足以使学习器发生显著变化,此时偏差主导了泛化误差,称为“欠拟合”,如果增加模型的复杂度,学习器的拟合能力增强,训练数据的变化被学习器学到,方差逐渐主导泛化误差;如果模型非常复杂,学习器的拟合能力已经非常强了,训练数据发生轻微的变化就会导致学习器结果发生显著变化,则发生“过拟合”。
🕒 8. 模型评价
🕘 8.1 已知推已知
训练精度(training accuracy)
- 在整个数据集上训练模型
- 并在同一个数据集上测试模型,得到模型的预测结果,和真实结果做比较,计算模型的精度
问题:
- 机器学习的目标是期望模型能在学习样例之外的数据上有好的表现(面向未来,而不是过去)
- 最大化训练精度,通常会产生过于复杂的模型,从而导致过拟合,模型不能很好地泛化
不同复杂度模型的泛化能力:
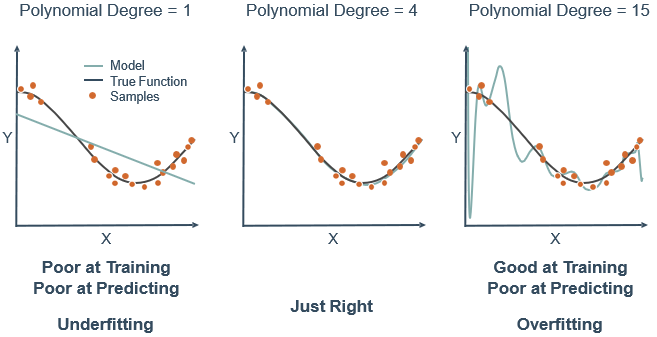
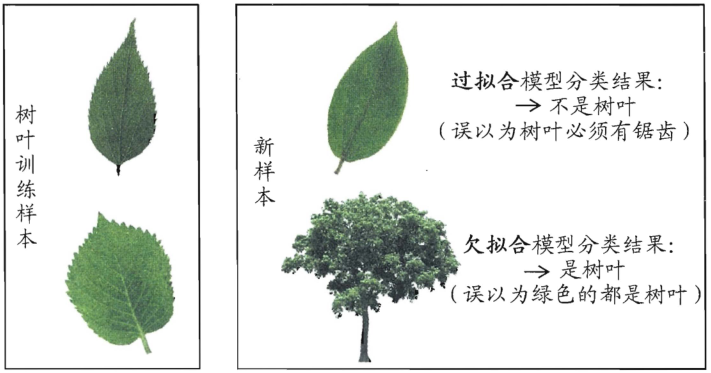
可以看到,欠拟合和过拟合都会导致较大的泛化误差。
🕘 8.2 已知推未知
测试精度(testing accuracy)
- 把数据集划分成两个子集:训练集和测试集
- 在训练集上训练模型
- 在测试集上测试模型,得出的模型与真实值比较,计算精度(即误差)
一般来说,测试集和训练集是互斥的,即测试样本不出现在训练集中。举个例子,你有个朋友很喜欢刷高考数学历年真题,结果月考的时候恰好老师就出了这些题(即上面的已知推已知),你的朋友大喜过望的和你炫耀。这里就不能判断出学生学得到底好不好,因为像这个朋友因为练习过就考了高分(即训练集上的效果好),结果高考来了,你的朋友发现并没有像遇见22个老朋友一样(此处diss一下@朱昊鲲),心情十分低落(即缺乏举一反三能力,也就是泛化能力不佳)。我们希望得到泛化能力强的模型,就好比希望学生对课程学得好,获得举一反三的能力。训练样本相当于给学生练习的习题,测试过程就相当于考试。显然,若测试样本被用作训练了,则会得到过于“乐观”的结果。
综上可知,每个模型在训练集上可以得到一个训练误差,在每个测试集上得到一个测试误差。我们认为最佳的模型是其在测试集上的测试误差越小越好。为了使测试误差最小化,训练误差是否越小越好呢?
在实际中,我们希望得到的是在新样本上预测能力最佳的模型,也就是模型在测试集上的误差越小越好。为了达到这个目的,应该从训练集中尽可能学出适用于所有潜在数据的普遍规律,训练误差越小越好。
然而,当模型使得训练误差越来越小的时候,很可能把训练集自身的一些特点当作了所有潜在数据都会有的性质,这样就会导致模型缺乏举一反三能力(就像机械刷题),即泛化能力下降,这种现象在机器学习中称为过拟合(overfitting)。与过拟合相对的是欠拟合(underfitting),指对训练样本的一般性质尚未学习好。
简而言之,并非在训练集上误差越小的模型,其预测能力就最佳,需要同时兼顾在训练集上的训练误差和在测试集上的测试误差。
🕤 8.2.1 语法
导入划分训练集和测试集的函数:
from sklearn.model_selection import train_test_split
划分数据集,测试集数据占全集的30%:
train, test = train_test_split(data, test_size=0.3)
在线文档:🔎 划分训练集和测试集的库
🕒 9. 交叉验证
继续前面刷题的例子,仅凭一次月考的成绩(单一数据集)就对模型的好坏进行评判显然是不合理的,因为很容易翻车,所以接下来引出交叉验证法的概念。
- 将数据集随机分为互斥的k个子集,每个子集都尽可能保持数据分布的一致性,即每个子集仍然要进行分层采样。
- 将k个子集随机分为k-1个子集为一组,剩下一个子集为另一组,有k种分法。
- 将每一种分组结果中k-1个子集的组当作训练集,另外一个当作测试集,这样就产生了k次预测,对k次预测结果的评分取平均,就得到了对该模型的总的评分。
交叉验证法评估结果的稳定性和保真性在很大程度上取决于k的取值,因此通常把交叉验证法称为“k折交叉验证”(k-fold crossvalidation)
例如,10折交叉验证如下图所示
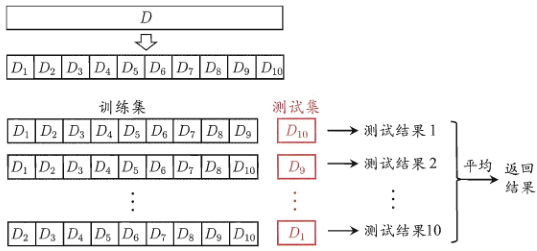
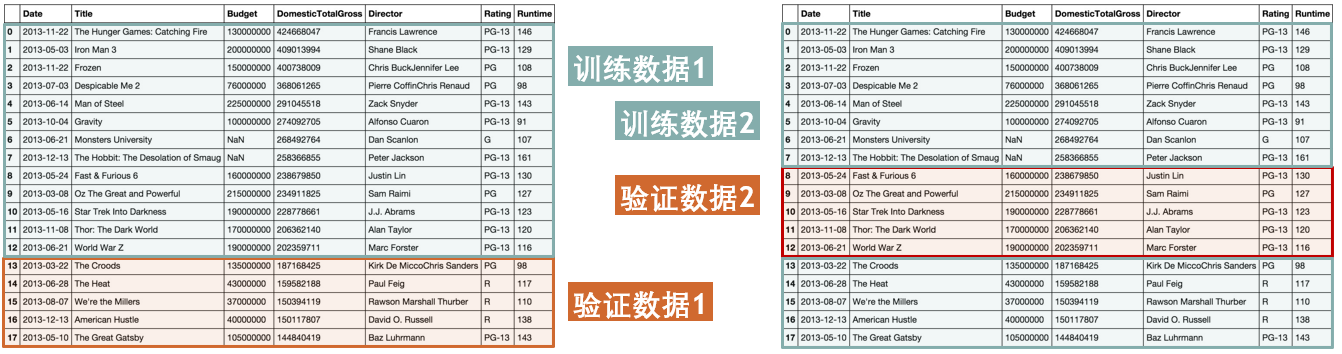
打个比方,交叉验证就像你高三的一轮复习,第一周复习立体几何,第二周复习等差数列(训练数据1)…,但是周测是高考历年真题卷(验证数据1),一个月后,你自信满满的觉得复习好了,把高考历年真题卷(训练数据2)都刷了一遍,结果月考出了道第二周复习时老师讲过的原题(验证数据2),不巧你早忘了怎么做,这就说明学习能力尚需加强。
🕘 9.1 语法
导入划分训练集和测试集的函数:
from sklearn.model_selection import cross_val_score
用一个给定的模型执行交叉验证:
cross_val = cross_val_score(KNN, X_data, y_data, cv=4,scoring='neg_mean_squared_error')
在线文档:🔎 交叉验证的库
cv的可能取值:
None, to use the default 3-fold cross validation,
integer, to specify the number of folds in a (Stratified)KFold,
CV splitter,
An iterable yielding (train, test) splits as arrays of indices.
其他CV splitter:
LeaveOneOut, ShuffleSplit, StratifiedShuffleSplit ……
在线文档:🔎 交叉验证:评估评估器性能
sklearn.datasets 模块主要提供一些导入、在线下载及本地生成数据集的方法,可以通过 dir 或 help 命令查看,会发现主要有三种形式:load_<dataset_name>、fetch_<dataset_name> 及 make_<dataset_name> 的方法。
- 自带的小数据集(packaged dataset):sklearn.datasets.load_
- 可在线下载的数据集(Downloaded Dataset):sklearn.datasets.fetch_
- 计算机生成的数据集(Generated Dataset):sklearn.datasets.make_
svmlight/libsvm格式的数据集:sklearn.datasets.load_svmlight_file(…)- 从买了data.org在线下载获取的数据集:sklearn.datasets.fetch_mldata(…)
🕒 10. 综合案例——鸢尾花分类
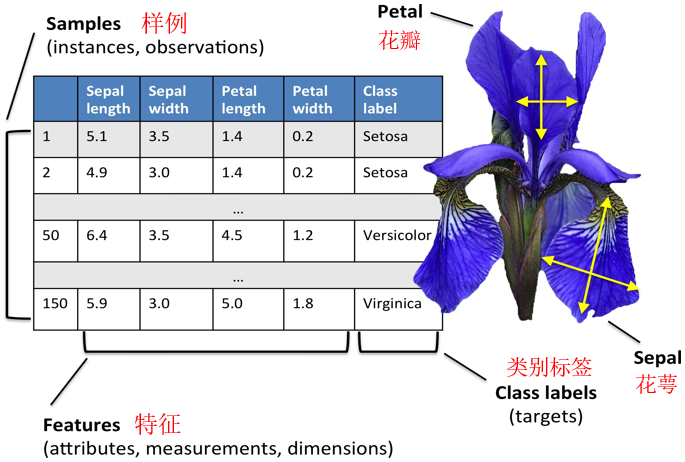
iris数据集介绍:
- 150个鸢(yuān)尾花样例
- 来自3个不同的属种
Setosa, Versicolor, Virginica
每种50个样例 - 用4个特征度量
花萼的长度和宽度,花瓣的长度和宽度
分类问题:给定一株鸢尾花,判定其属种
创建机器学习应用路线图
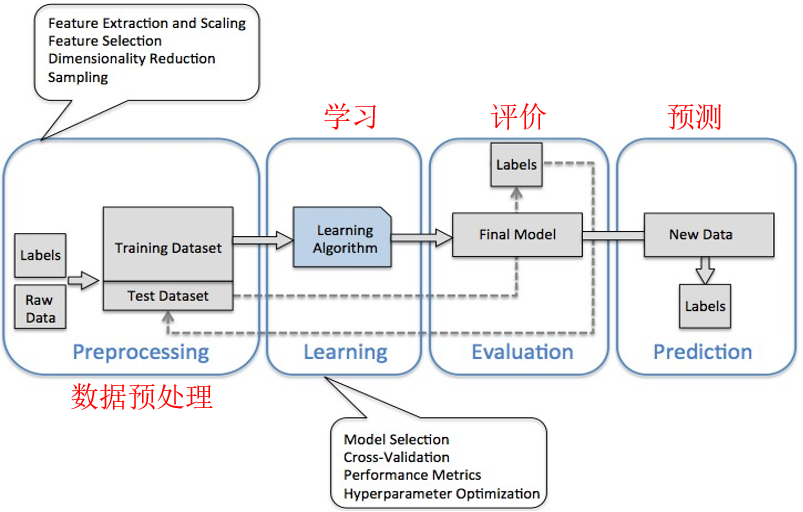
首先导入库
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
接着装载数据集,数据集的形式是Pandas的DataFrame
url = "iris.csv"
# 为数据集分配列名
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']
# 将数据集读取到pandas的dataframe
dataset = pd.read_csv(url, names=names)
dataset.head() # 查看数据集的前5行
sepal-length sepal-width petal-length petal-width Class 0 5.1 3.5 1.4 0.2 Iris-setosa 1 4.9 3.0 1.4 0.2 Iris-setosa 2 4.7 3.2 1.3 0.2 Iris-setosa 3 4.6 3.1 1.5 0.2 Iris-setosa 4 5.0 3.6 1.4 0.2 Iris-setosa \begin{array}{|l|l|l|l|l|l|} \hline & \text { sepal-length } & \text { sepal-width } & \text { petal-length } & \text { petal-width } & \text { Class } \\ \hline \mathbf{0} & 5.1 & 3.5 & 1.4 & 0.2 & \text { Iris-setosa } \\ \hline \mathbf{1} & 4.9 & 3.0 & 1.4 & 0.2 & \text { Iris-setosa } \\ \hline \mathbf{2} & 4.7 & 3.2 & 1.3 & 0.2 & \text { Iris-setosa } \\ \hline \mathbf{3} & 4.6 & 3.1 & 1.5 & 0.2 & \text { Iris-setosa } \\ \hline \mathbf{4} & 5.0 & 3.6 & 1.4 & 0.2 & \text { Iris-setosa } \\ \hline \end{array} 01234 sepal-length 5.14.94.74.65.0 sepal-width 3.53.03.23.13.6 petal-length 1.41.41.31.51.4 petal-width 0.20.20.20.20.2 Class Iris-setosa Iris-setosa Iris-setosa Iris-setosa Iris-setosa
把数据集分解成属性(X)和标签(y),使用Pandas的纵向切割方法。
X = dataset.iloc[:, :-1].values # 取行索引为全部,列索引从开始到最后一个的前一个的数据。
y = dataset.iloc[:, 4].values # 取行索引为全部,列索引从开始到第3个的数据。
iloc[ ]函数(Pandas库)介绍
作用:对数据进行位置索引,从而在数据表中提取出相应的数据。
使用:
df.iloc[a,b]:其中df是DataFrame数据结构的数据,a是行索引(从0开始),b是列索引(从0开始)。含义是取行索引为a列索引为b的数据。df.iloc[a:b,c]:取行索引从a到b-1,列索引为c的数据。注意:在iloc中a:b是左到右不到的,即lioc[1:3,:]是从行索引从1到2,所有列索引的数据。iloc[].values,用values属性取值,返回ndarray,但是单个数值无法用values函数读取。 如果不带values则表示数据结构是Seriesiloc[a:b,c:d]:取行索引从a到b-1,列索引从c到d-1的数据。iloc[:,:d]:取行索引为全部,列索引从开始到d-1的数据。
把数据集划分成训练集和测试集,80%的数据划分到训练集,20%的数据划分到测试集。
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)
原始数据的取值范围变化很大,有必要对数据进行规范化处理,在这里对属性X进行缩放。
欧式距离需要在规范化的数据上运算,才能给出正确的结果。而梯度下降算法(神经网络的训练方法)在规范化的数据上收敛得更快。
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
对模型进行训练
from sklearn.neighbors import KNeighborsClassifier
classifier = KNeighborsClassifier(n_neighbors=5)
classifier.fit(X_train, y_train)
# 当前训练器的参数:KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',metric_params=None, n_jobs=None, n_neighbors=5, p=2,weights='uniform')
# 注:当p=1时,是曼哈顿距离;p=2时,是欧式距离;p=∞时,是切比雪夫距离
在测试集上进行预测
y_pred = classifier.predict(X_test)
为评估一个模型的优劣,可以使用混淆矩阵,以及准确率、召回率和F1评分等指标。
from sklearn.metrics import classification_report, confusion_matrix
print(confusion_matrix(y_test, y_pred))
print(classification_report(y_test, y_pred))
[ [ 8 0 0 ] [ 0 9 1 ] [ 0 1 11 ] ] [ \ [ \ 8 \ 0 \ \ 0 \ ] \\ \ \ [ \ 0 \ 9 \ \ 1\ ] \\ \ \ [ \ 0 \ 1 \ 11 \ ] \ ] [ [ 8 0 0 ] [ 0 9 1 ] [ 0 1 11 ] ]
precision recall f1-score support Iris-setosa 1.00 1.00 1.00 8 Iris-versicolor 0.90 0.90 0.90 10 Iris-virginica 0.92 0.92 0.92 12 accuracy 0.93 30 macro avg 0.94 0.94 0.94 30 weighted avg 0.93 0.93 0.93 30 \begin{array}{rrrrr} & \text { precision} & \text { recall} & \text { f1-score } & \text { support } \\ \text { Iris-setosa } & 1.00 & 1.00 & 1.00 & 8 \\ \text { Iris-versicolor } & 0.90 & 0.90 & 0.90 & 10 \\ \text { Iris-virginica } & 0.92 & 0.92 & 0.92 & 12 \\ \text { } & & & & \\ \text { accuracy } & & &0.93 &30 \\ \text { macro avg } & 0.94 & 0.94 & 0.94 & 30 \\ \text { weighted avg } & 0.93 & 0.93 & 0.93 & 30 \end{array} Iris-setosa Iris-versicolor Iris-virginica accuracy macro avg weighted avg precision1.000.900.920.940.93 recall1.000.900.920.940.93 f1-score 1.000.900.920.930.940.93 support 81012303030
输出的混淆矩阵显示,只有一个样本分类错误。分类器的各项中,三个类别都达到很高的准确率和召回率,获得超过0.90的Fl评分。
在KNN算法中,什么样的参数K能够获得较好的分类效果(准确率)呢?我们可以把K的各种可能取值及其对应的分类误差率绘制在一张图上。在这里,我们选择的K的取值范围为[1,40]。
error = []
# 计算K值在1和40之间的误差
for i in range(1, 40):
knn = KNeighborsClassifier(n_neighbors=i)
knn.fit(X_train, y_train)
pred_i = knn.predict(X_test)
error.append(np.mean(pred_i != y_test))
画图
plt.figure(figsize=(12, 6))
plt.plot(range(1, 40), error, color='red', linestyle='dashed', marker='o',
markerfacecolor='blue', markersize=10)
plt.title('Error Rate K Value')
plt.xlabel('K Value')
plt.ylabel('Mean Error')
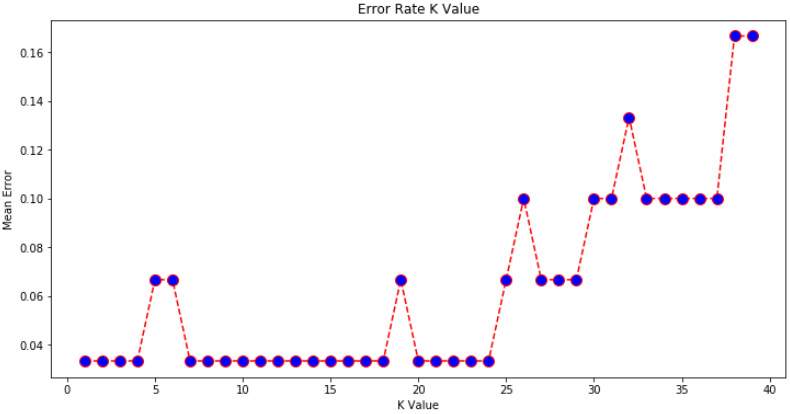
当K取值在[1,4]、[7,18] 和 [20, 24]的时候,分类器的错误率最低。所以取其中的任何一个值,作为模型的K参数,都是可以的。
Scikit-learn是利用model_selection模块中的cross_val_score函数来实现交叉验证的。下面我们在 iris数据集上对 KNeighborsClassifier模型使用交叉验证进行评估。
from sklearn import datasets
iris_dataset = datasets.load_iris() # 导入iris数据集
X = iris_dataset.data
y = iris_dataset.target
X.shape, y.shape
# 输出:((150, 4), (150,))
from sklearn.model_selection import cross_val_score # 导入K折交叉验证模块
knn = KNeighborsClassifier(n_neighbors=5) # 建立一个5近邻模型
# 进行10折交叉验证,即把样本分成10份,每一份都作为测试集,得到10次预测精度
scores = cross_val_score(knn, X, y, cv=10, scoring='accuracy')
print(scores)
[ 1. 0.93333333 1. 1. 0.86666667 0.93333333 0.93333333 1. 1. 1. ] [ \ 1. \hspace{2cm} 0.93333333 \hspace{0.2cm} 1. \hspace{2cm} 1. \hspace{2cm} 0.86666667 \hspace{0.3cm} 0.93333333 \\ \hspace{0.2cm} 0.93333333 \hspace{0.6cm} 1. \hspace{1.6cm} 1. \hspace{2cm} 1. \hspace{2cm} ] [ 1.0.933333331.1.0.866666670.933333330.933333331.1.1.]
# 将10次预测精度的平均值打印出来
print(scores.mean())
# 输出:0.966666666667
选取最优的K值,训练不同K值的K近邻模型,得到其10折交叉验证的预测精度值,最后通过绘制精度随K值变化的图来选择精度最高的K值
k_range = list(range(1, 31))
k_scores = []
for k in k_range:
knn = KNeighborsClassifier(n_neighbors=k)
scores = cross_val_score(knn, X, y, cv=10, scoring='accuracy')
k_scores.append(scores.mean())
print(k_scores)
[ 0.95999999999999996 , 0.95333333333333337 , 0.96666666666666656 , 0.96666666666666656 , 0.96666666666666679 , 0.96666666666666679 , 0.96666666666666679 , 0.96666666666666679 , 0.97333333333333338 , 0.96666666666666679 , 0.96666666666666679 , 0.97333333333333338 , 0.98000000000000009 , 0.97333333333333338 , 0.97333333333333338 , 0.97333333333333338 , 0.97333333333333338 , 0.98000000000000009 , 0.97333333333333338 , 0.98000000000000009 , 0.96666666666666656 , 0.96666666666666656 , 0.97333333333333338 , 0.95999999999999996 , 0.96666666666666656 , 0.95999999999999996 , 0.96666666666666656 , 0.95333333333333337 , 0.95333333333333337 , 0.95333333333333337 ] \begin{array}{lll} {[0.95999999999999996,} & 0.95333333333333337, & 0.96666666666666656, \\ 0.96666666666666656, & 0.96666666666666679, & 0.96666666666666679, \\ 0.96666666666666679, & 0.96666666666666679, & 0.97333333333333338, \\ 0.96666666666666679, & 0.96666666666666679, & 0.97333333333333338, \\ 0.98000000000000009, & 0.97333333333333338, & 0.97333333333333338, \\ 0.97333333333333338, & 0.97333333333333338, & 0.98000000000000009, \\ 0.97333333333333338, & 0.98000000000000009, & 0.96666666666666656, \\ 0.96666666666666656, & 0.97333333333333338, & 0.95999999999999996, \\ 0.96666666666666656, & 0.95999999999999996, & 0.96666666666666656, \\ 0.95333333333333337, & 0.95333333333333337, & 0.95333333333333337] \end{array} [0.95999999999999996,0.96666666666666656,0.96666666666666679,0.96666666666666679,0.98000000000000009,0.97333333333333338,0.97333333333333338,0.96666666666666656,0.96666666666666656,0.95333333333333337,0.95333333333333337,0.96666666666666679,0.96666666666666679,0.96666666666666679,0.97333333333333338,0.97333333333333338,0.98000000000000009,0.97333333333333338,0.95999999999999996,0.95333333333333337,0.96666666666666656,0.96666666666666679,0.97333333333333338,0.97333333333333338,0.97333333333333338,0.98000000000000009,0.96666666666666656,0.95999999999999996,0.96666666666666656,0.95333333333333337]
import matplotlib.pyplot as plt
# 绘制KNN的K值(x轴)与交叉验证精度(y轴)
plt.plot(k_range, k_scores)
plt.xlabel('Value of K for KNN')
plt.ylabel('Cross-Validated Accuracy')
plt.show()
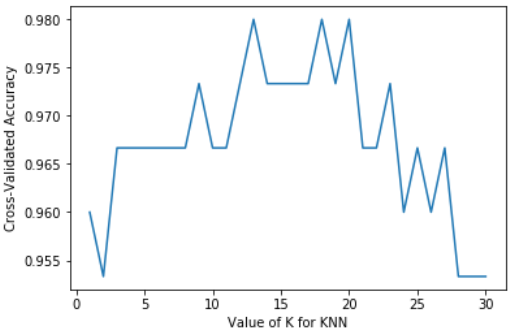
🕒 11. 课后习题
- 【单选题】为了对某类数据进行分类,采集了一批数据,保存在数据框架dataset中,dataset内数据总数为560,将dataset分解成X(特征)和y标签后,执行以下python程序:
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
scaler = StandardScaler()
scaler.fit(X)
X = scaler.transform(X)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)
K = [1, 25, 400]
for i in K:
classifier = KNeighborsClassifier(n_neighbors=i)
classifier.fit(X_train, y_train)
y_pred = classifier.predict(X_test)
print('当K=%d时,训练集准确率为%0.3f,验证集准确率为%0.3f' %
(i,classifier.score(X_train, y_train),classifier.score(X_test, y_test)))
输出结果为:
k=1:训练集准确率为1.000,验证集准确率为0.895
k=25:训练集准确率为0.949,验证集准确率为0.947
k=400:训练集准确率为0.629,验证集准确率为0.623
对输出结果的分析,以下( )更合理。
A. 训练所得的三个模型中,K=1时的模型最好,K=25时的模型欠拟合,K=400时的模型过拟合。
B. 训练所得的三个模型中,K=25时的模型最好,K=1时的模型欠拟合,K=400时的模型过拟合。
C. 训练所得的三个模型中,K=25时的模型最好,K=400时的模型欠拟合,K=1时的模型过拟合。
D. 训练所得的三个模型中,K=1时的模型最好,K=400时的模型欠拟合,K=25时的模型过拟合。
-
【判断题】机器学习中,如发生过拟合现象,可在分析过拟合产生原因基础上,尝试采取降低模型复杂度、引入正则化项等措施提高模型泛化性能,如减少模型的参数个数(去除非重要特征)等。
-
【判断题】在同一训练集上,经过机器学习训练出来的不同模型中,训练误差越小的模型越好。
-
【判断题】机器学习中,预测能力好的模型才是好模型。
-
【判断题】机器学习中,如发生欠拟合现象,可在分析欠拟合产生原因基础上,尝试采取增加新特征、使用模型容量(拟合各种函数能力)大的模型等措施提高模型拟合能力,如使用深度学习模型等。
答案:1.C 2.√ 3.×(好比只会做真题而不会做模拟题) 4.√ 5.√
推荐书籍:《机器学习》周志华
推荐视频:
(强推|双字)2022吴恩达机器学习Deeplearning.ai课程
人工智能教程(100讲)之 用K近邻来进行分类
参考文章:🔎 一文搞懂k近邻(k-NN)算法(一)
OK,以上就是本期知识点“K近邻与模型选择”的知识啦~~ ,感谢友友们的阅读。后续还会继续更新,欢迎持续关注哟📌~
💫如果有错误❌,欢迎批评指正呀👀~让我们一起相互进步🚀
🎉如果觉得收获满满,可以点点赞👍支持一下哟~
❗ 转载请注明出处
作者:HinsCoder
博客链接:🔎 作者博客主页




![[python][学习]循环与嵌套---打印乘法口诀](https://img-blog.csdnimg.cn/05e15267dbd841d392683f07ecc61909.png)