12.1排序

news2025/1/11 11:16:07

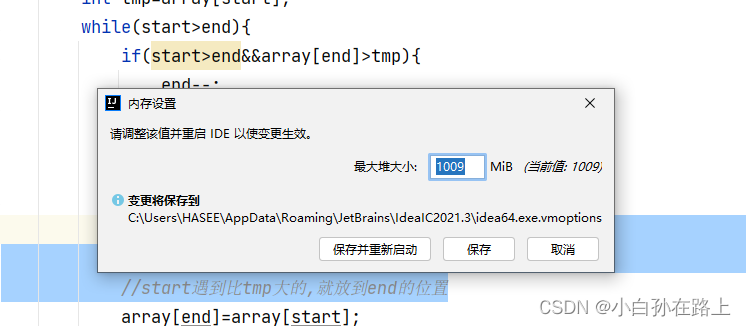
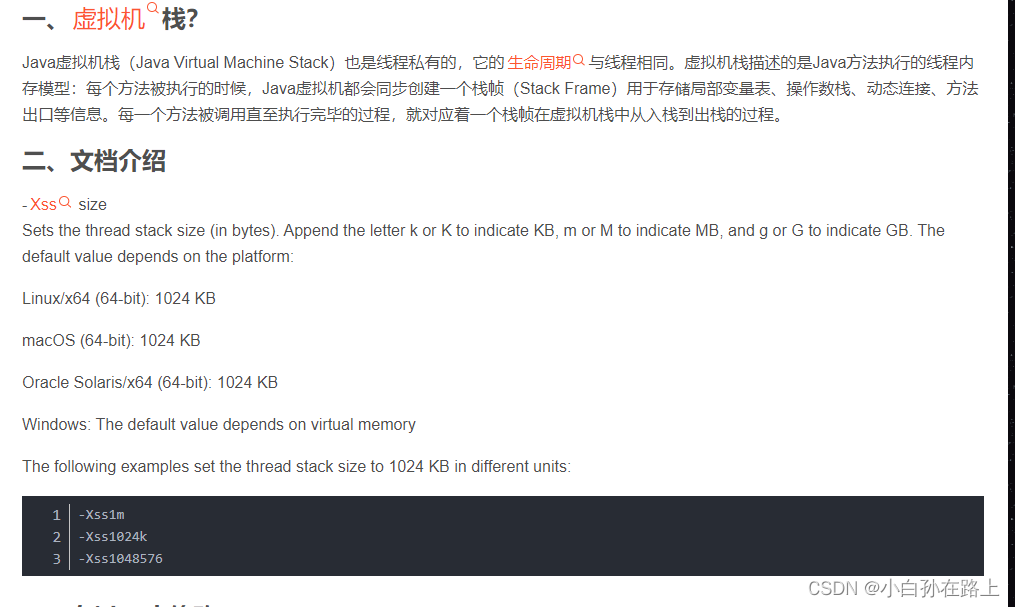
0.修改栈堆内存

一.堆排序

1 原理

2.代码实现

3.分析

二.冒泡排序

1 原理

2.实现

3.分析

三.快速排序(重要)

1 原理-总览

2.方法:挖坑法

步骤一

步骤二

步骤三

步骤四

步骤五

步骤六

3.代码实现挖坑法

4.分析

四.字符串转整数

1.字符串方法

2.字符数组方法

3.sb方法

五.笔试强训

0.修改栈堆内存

一.堆排序

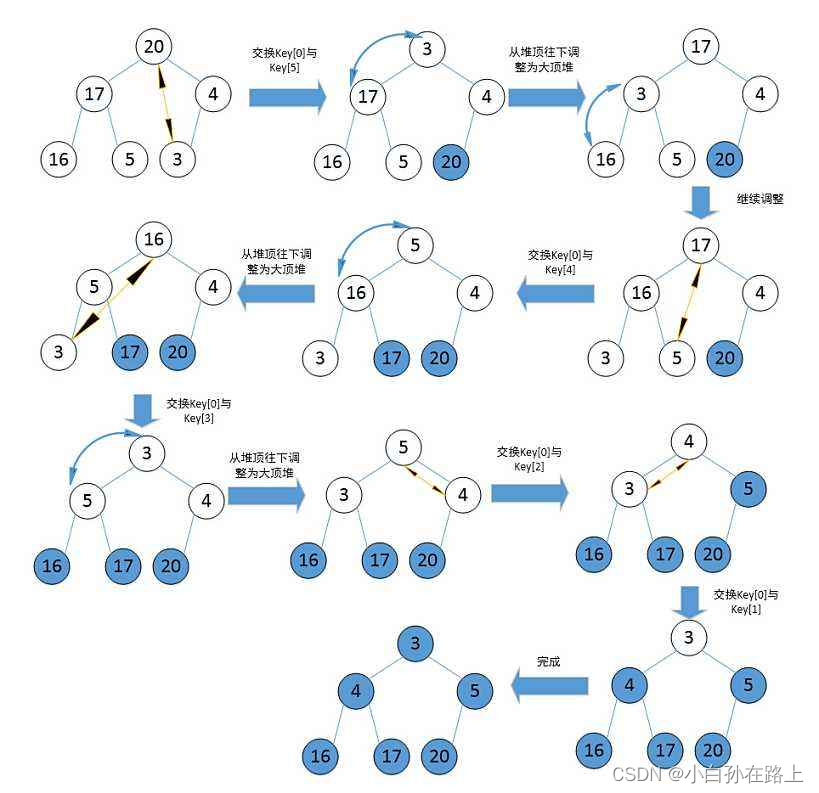
1 原理

基本原理也是选择排序，只是不在使用遍历的方式查找无序区间的最大的数，而是通过堆来选择无序区间的最大的数。

注意：排升序要建大堆；排降序要建小堆

2.代码实现

/**
 * 堆排序
 */
public static void heapSort(int[] array){
    createHeap(array);
    int end=array.length-1;
    while(end>0){//等于0的时候就不需要调整了
        swap(array[0],array[end]);
        shiftDown(array,0,end);
        end--;
    }
}
public static void createHeap(int[] array) {
    for (int parent =(array.length-1-1)/2; parent >=0 ; parent--) {
        shiftDown(array,parent,array.length);
    }
}
public static void shiftDown(int[] array,int parent,int len){
    int child=parent*2+1;

    while(child<len){
        if(child+1<len&&array[child]<array[child+1]){
            child++;
        }
        if(array[child]>array[parent]){
            swap(array[child],array[parent]);
            parent=child;
            child=parent*2+1;
        }else{
            break;
        }
    }
}

3.分析

/**
 * 堆排序
 */
/**
 * 时间复杂度：O(N * log N)
 *
 * 空间复杂度：O(1)
 *
 * 稳定性：不稳定
 *
 * 面试 写堆排序  就是 写的调整过程
 *
 * @param array
 */

因为要遍历每个元素所以就是n然后最坏情况下要从上往下一直调整就是树的高度logn

所以就是时间复杂度：O(N * log N)

二.冒泡排序

1 原理

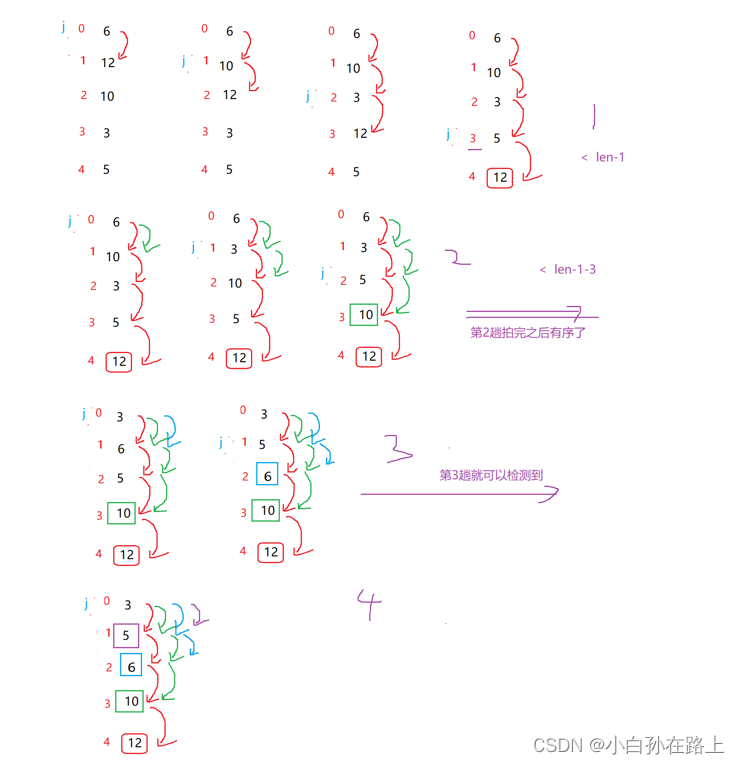
在无序区间，通过相邻数的比较，将最大的数冒泡到无序区间的最后，持续这个过程，直到数组整体有序

2.实现

/**
 * 冒泡排序
 */
public static void bubbleSort(int[] array) {
    for (int i = 0; i < array.length; i++) {
        //int max=i;
        int j = i+1;
        boolean flg=true;
        for (; j < array.length-i-1; j++) {
            if(array[j]>array[j+1]){
                swap(array[j],array[j+1]);
                flg=false;
            }
        }
        if(flg) return;
    }
}

3.分析

/**
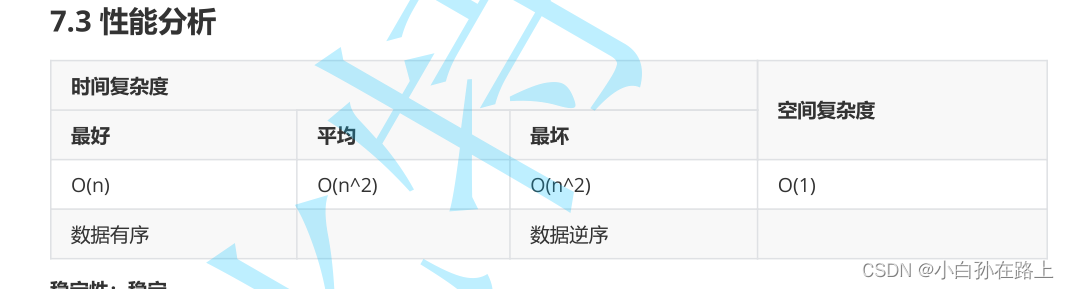
 * 冒泡排序
 * 时间复杂度：O(N^2)
 * 有序情况下：O(n)
 * 空间复杂度：O(1)
 * 稳定性：稳定的排序
 * @param array
 */

三.快速排序(重要)

1 原理-总览

从待排序区间选择一个数，作为基准值(pivot)；
Partition: 遍历整个待排序区间，将比基准值小的（可以包含相等的）放到基准值的左边，将比基准值大的（可

以包含相等的）放到基准值的右边；

3. 采用分治思想，对左右两个小区间按照同样的方式处理，直到小区间的长度 == 1，代表已经有序，或者小区间

的长度 == 0，代表没有数据。

2.方法:挖坑法

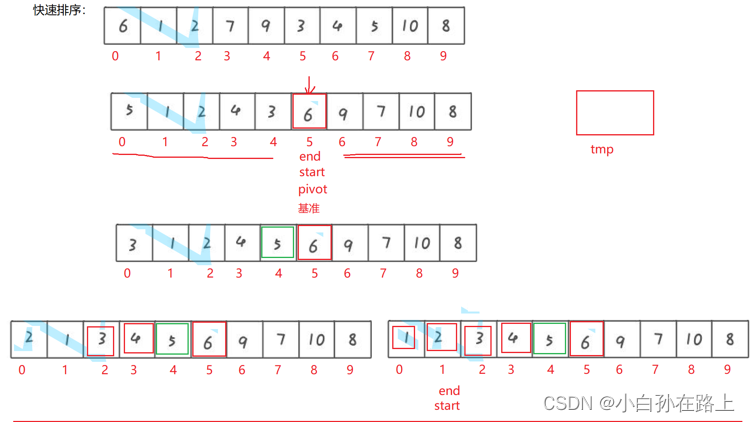
步骤一

先定义数组第一个元素tmp.挖坑

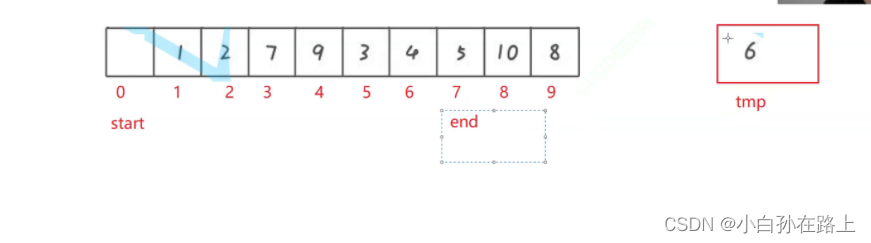
步骤二

再定义两个指针一个是end另外一个是start

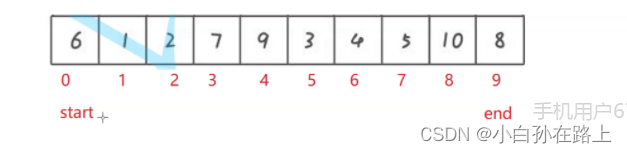
步骤三

遍历end 如果比tmp大的end就往右移也就是end--

遇到比tmp小的就放到坑里

停止遍历

步骤四

遍历start,遇到比tmp小的就左移,也就是start++

遇到比tmp大的就放在end所在坑里

停止遍历

步骤五

直到start与end相遇那么这个位置放入tmp的值,

这个位置也是基准

这样就发现基准的左边就比他小.基准的右边就比他大

步骤六

分而治之,再次递归.分别对基准的左边和右边做同样的行为

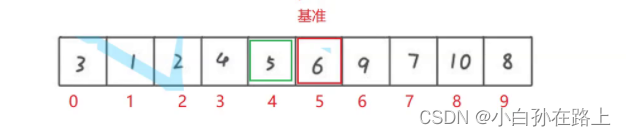
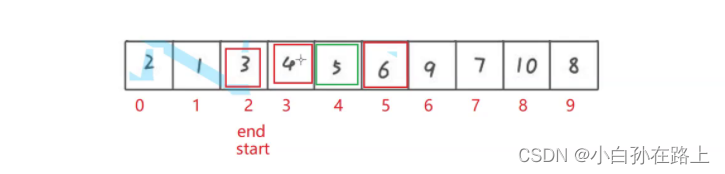
再次递归发现.3右边只有一个元素或者没有元素,就代表有序了.4默认有序

3.代码实现挖坑法

第一步快排的时候需要找基准

第二步,分别递归左边和右边

左边:

右边

第三步递归结束条件

也就是left>=right

/**
 * 快速排序
 */
public static void quickSort(int[] array) {
    quick(array,0,array.length-1);
}
public static void quick(int[]array,int left,int right){
    if(left>=right) return;

    int pivot=partition(array,left,right);

    quick(array,left,pivot-1);//分支左边
    quick(array,pivot+1,right);
}
public static int partition(int[] array,int start,int end){
    int tmp=array[start];
    while(start>end){
        if(start>end&&array[end]>tmp){
            end--;
        }
        //end遇到tmp小的,就放到start的位置
        array[start]=array[end];
        if(start>end&&array[start]<=tmp){
            start++;
        }
        //start遇到比tmp大的,就放到end的位置
        array[end]=array[start];
    }
    //到这里,start与end相遇
    array[start]=tmp;
    return start;
}

4.分析

每一层都需要n 一共有logn 所以就是相乘

空间复杂度就是

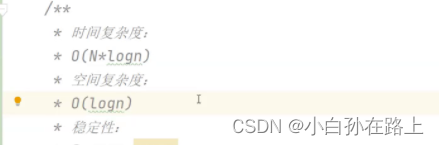
  * 时间复杂度：
       * 最好【每次可以均匀的分割待排序序列】：O(N*logn)
* 最坏：数据有序 或者逆序的情况 O(N^2)
* 空间复杂度：
       * 最好：O(logn)
* 最坏：O(n)   单分支的一棵树
* 稳定性：不稳定的排序
* @param array
*/

最坏的情况下就是有序的树,

他是数据敏感的

跟对排类似,但是前面的k要小

如果对空间复杂度没有要求.用快排

对空间复杂度又要求用堆排或者归并

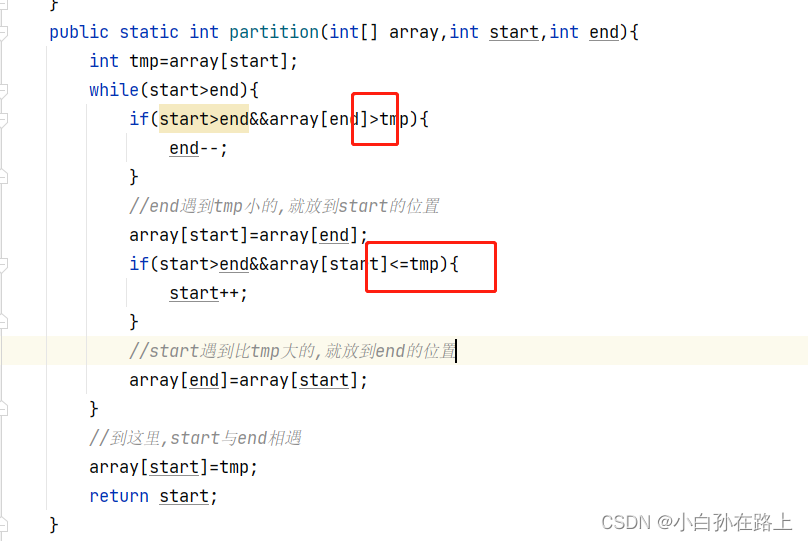
不可以不取等号

不然的话,遇到两个数相等的情况,进不了if语句

end和start就一直互相换

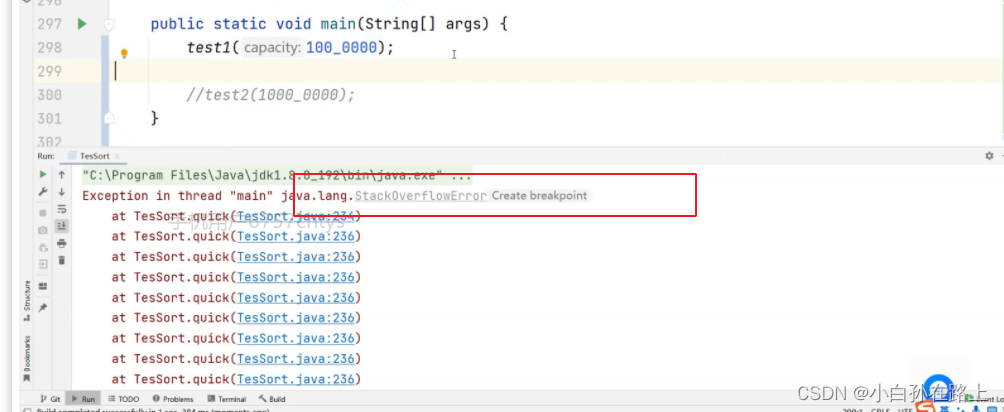
因为递归需要在栈上开辟内存,

idea可以设置栈的大小

四.字符串转整数

先看几种情况

字符串底层是一个数组

是被final修饰不可以改.

字符串转整数如果用自带的方法就是

Integer.valueof(String)

如果自己用就是

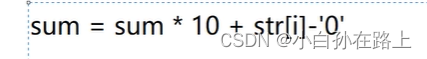
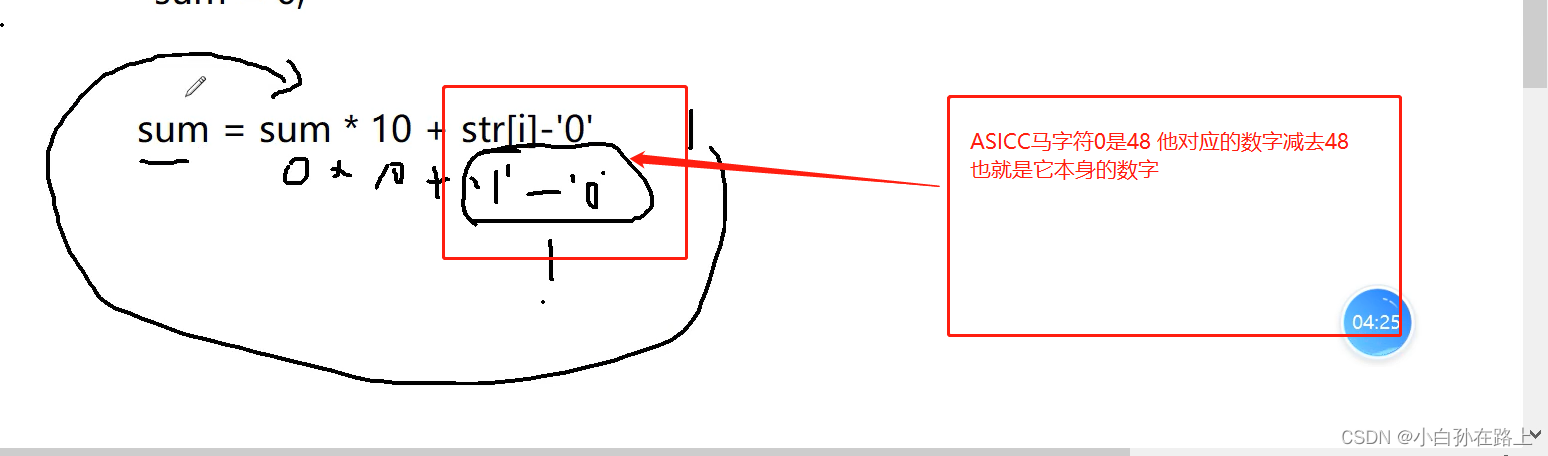
要注意这两种情况的关系

一个是不指向任何对象.一个是有对象,但是对象里面是空的

1.字符串方法

import java.util.*;
public class Main{
    public static void main(String[] args){
        Scanner sc=new Scanner(System.in);
        while(sc.hasNext()){
            String str=sc.nextLine();
            if(str==null||str.isEmpty()) return;
            int flg=0;
            if(str.charAt(0)=='+'){
                flg=1;
            }
            if(str.charAt(0)=='-'){
                flg=-1;
            }
            int sum=0;
            for(int i=0;i<str.length();i++){
                if(i==0){
                    if(flg==0){
                      if(str.charAt(i)<'0'||str.charAt(i)>'9'){
                          //System.out.println(sum);
                        break;
                      }
                        if(str.charAt(i)==0){
                            break;
                        }
                      sum=(str.charAt(i)-'0');
                    }
                }else{
                   if(str.charAt(i)<'0'||str.charAt(i)>'9'){
                        sum=0;break;
                    }
                    sum=sum*10+(str.charAt(i)-'0');
                }
            }
            if(flg==0) flg=1;
            System.out.println(flg*sum);
        }
    }
}

因为字符串本身不能改变所以只能用这样的方式不停地比较.

如果用字符数组把第一个是+-号的改成0即可.

2.字符数组方法

import java.util.*;
public class Solution {
    public int StrToInt(String str) {
        //Scanner sc=new Scanner(System.in);
        if(str==null||str.isEmpty()) return 0;
            int sum=0;
          // String str=sc.nextLine();
           char[] arr=str.toCharArray();
            int flg=1;
            if(arr[0]=='+'){
              //  flg=1;
                arr[0]='0';
            }
            if(arr[0]=='-'){
                flg=-1;
                arr[0]='0';
            }
            for(int i=0;i<arr.length;i++){
                if(arr[i]<'0'||arr[i]>'9'){
                    sum=0; break;
                }
                sum=sum*10+arr[i]-'0';
            }
            return sum*flg;
        
    }
}

3.sb方法

import java.util.*;
public class Solution {
    public int StrToInt(String str) {
        if(str.length()==0) return 0;
    StringBuilder sb=new StringBuilder();
        if(str.charAt(0)!='+'&&str.charAt(0)!='-'){
            if(str.charAt(0)>='0'&&str.charAt(0)<='9'){
                sb.append(str.charAt(0));
            }else{
                return 0;
            }
         }//不是加减的情况
        int flg=1;
         if(str.charAt(0)=='-'){
            flg=-1;
        }
        for(int i=1;i<str.length();i++){
            if(str.charAt(i)<'0'||str.charAt(i)>'9'){
                return 0;
            }else{
                   sb.append(str.charAt(i));
                }
            }
       sb.reverse();
       int sum=0;
       int m=1;
       int n=0;
       for(int i=0;i<sb.length();i++){
            n=(int)sb.charAt(i)-48;
                sum+=n*m;
                m*=10;
         }
            return sum*flg;
    }
}