目录

实验十 符号计算基础与符号微积分

1.1实验目的

1.3流程图

1.4程序清单

1.5运行结果及分析

1.6实验的收获与体会

1.1实验目的

 

1.2实验内容

符号计算基础与符号微积分

课本第372页

1.3流程图

 

1.4程序清单

实验十

1

clear

x=sym('6');

y=sym('5');

z=(1+x)/(sqrt(3+x)-sqrt(y))

2

syms x y ;

t=sym('5135');

a=x^4+y^4;

factor(a)

factor(t)

3

clc

clear

syms bta1 bta2 x;

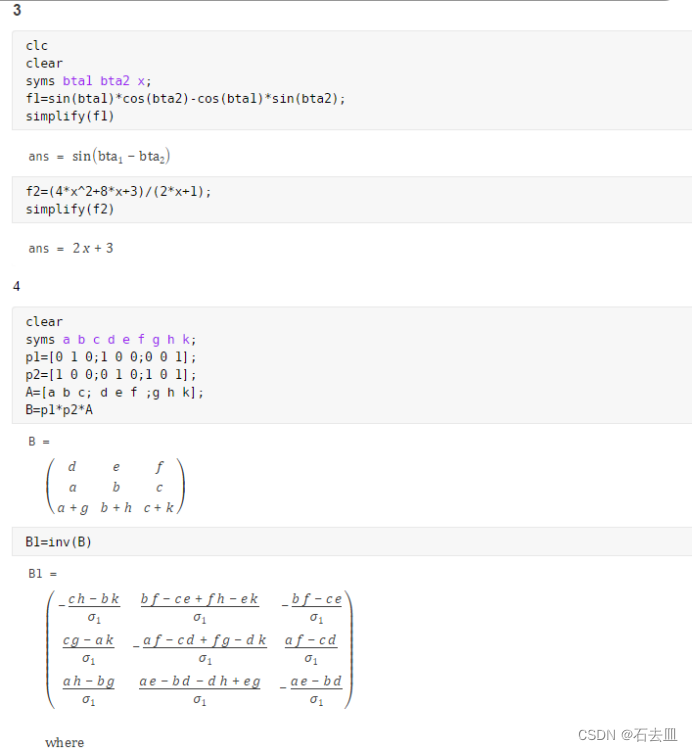
f1=sin(bta1)*cos(bta2)-cos(bta1)*sin(bta2);

simplify(f1)

f2=(4*x^2+8*x+3)/(2*x+1);

simplify(f2)

4

clear

syms a b c d e f g h k;

p1=[0 1 0;1 0 0;0 0 1];

p2=[1 0 0;0 1 0;1 0 1];

A=[a b c; d e f ;g h k];

B=p1*p2*A

B1=inv(B)

inv(B)*B

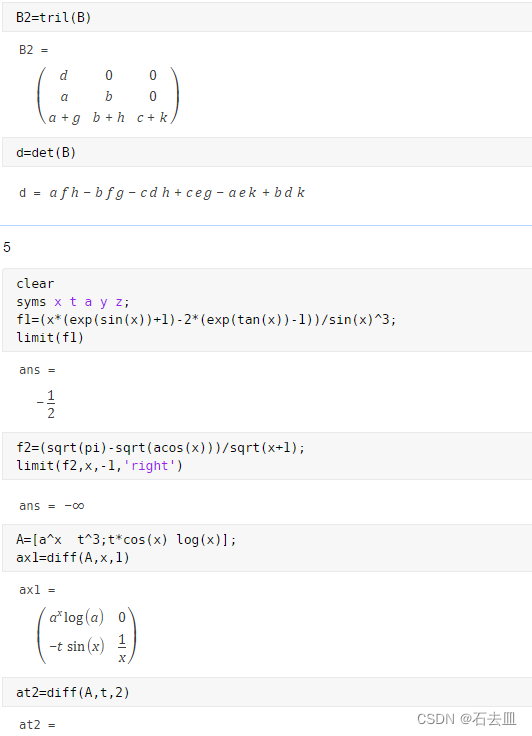
B2=tril(B)

d=det(B)

5

clear

syms x t a y z;

f1=(x*(exp(sin(x))+1)-2*(exp(tan(x))-1))/sin(x)^3;

limit(f1)

f2=(sqrt(pi)-sqrt(acos(x)))/sqrt(x+1);

limit(f2,x,-1,'right')

A=[a^x t^3;t*cos(x) log(x)];

ax1=diff(A,x,1)

at2=diff(A,t,2)

axt=diff(ax1,t)

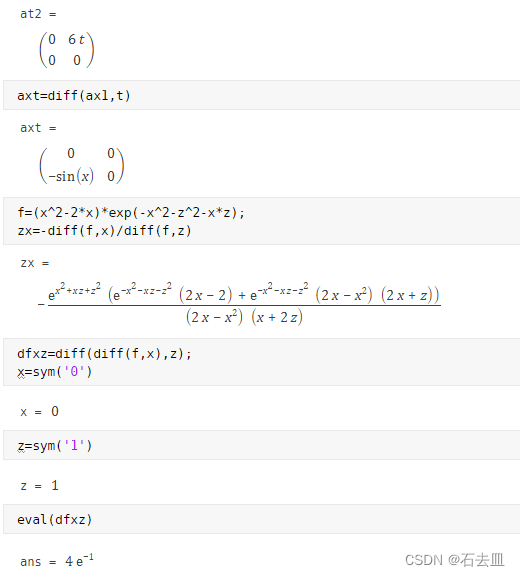
f=(x^2-2*x)*exp(-x^2-z^2-x*z);

zx=-diff(f,x)/diff(f,z)

dfxz=diff(diff(f,x),z);

x=sym('0')

z=sym('1')

eval(dfxz)

6

clc

clear

x=sym('x');

f1=1/(1+x^4+x^8);

f3=(x^2+1)/(x^4+1);

F1=int(f1)

F3=int(f3,0,inf)

1.5运行结果及分析

 

 

 

 

 

 

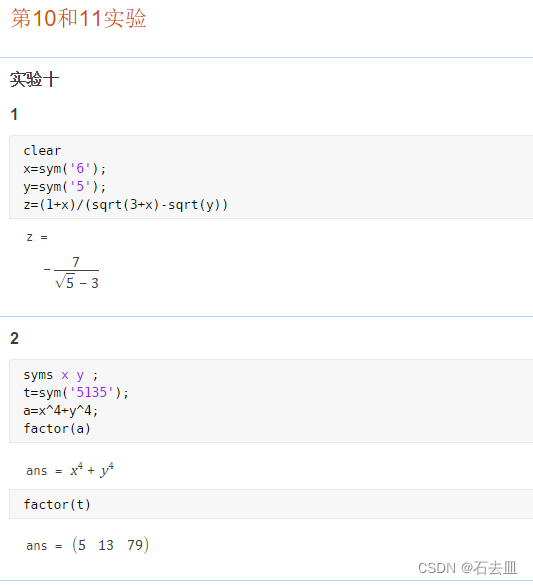
1.6实验的收获与体会

本次实验过后，我掌握了定义符号对象的方法和符号表达式的运算和求解的方法，同时也掌握了符号极限及导数、定积分不定积分的方法。

matlab是一个实用性很强，操作相对容易，比较完善的工具软件，使用起来比较方便，通过操作可以很快看到结果，能够清晰的感觉到成功与失败，虽然课程中也会出现一些小问题，但是很喜欢这门课程。

学习matlab体会最多的是这个软件的功能强大，好多数学题都被轻易的解出。但是有一点遗憾，不知是我不会用，还是它没个功能，已知空间的电荷分布，求空间的电场分布。其中电场分布是无法用函数表达式表示。我知道计算机肯定可以实现，但是这个软件能不能实现就不知道了，我看过许多资料，但是在这方面没有提到相关信息。

总之，经过这次实验收获很大，对学习帮助很大