leecode654——最大二叉树

news2024/10/6 0:37:43

leecode最大二叉树

🌻题目要求：

给定一个不重复的整数数组 nums 。最大二叉树可以用下面的算法从 nums 递归地构建:
创建一个根节点，其值为 nums 中的最大值。
递归地在最大值左边的子数组前缀上构建左子树。
递归地在最大值右边的子数组后缀上构建右子树。
返回 nums 构建的最大二叉树。

🌻思路一：递归

🌻思路二: 单调栈

使用递归虽然每次对数组进行了拆分，但是会对数组中的元素也进行多次遍历，那么会不会有一种方式，可以仅通过一次遍历就可以得出最终结果。
单调栈的思路：

🔵（1）如果栈顶元素大于待插入的元素，那么直接入栈；

🔵（2）如果栈顶元素小于待插入的元素，那么栈顶元素出栈

在对比节点的同时，也要进行二叉树得到构造，即：

🔵（1）如果栈顶元素大于待插入的元素，则栈顶元素.right=待插入元素

🔵（2) 如果栈顶元素小于待插入的元素，则待插入元素.left=栈顶元素。

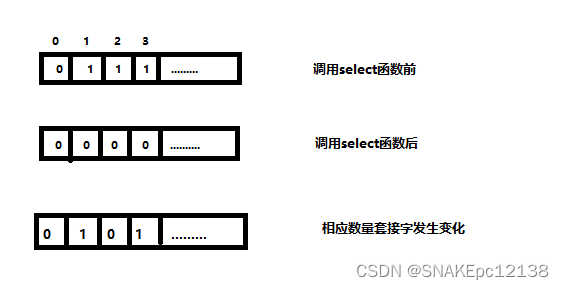
图来自：leecode大佬思路

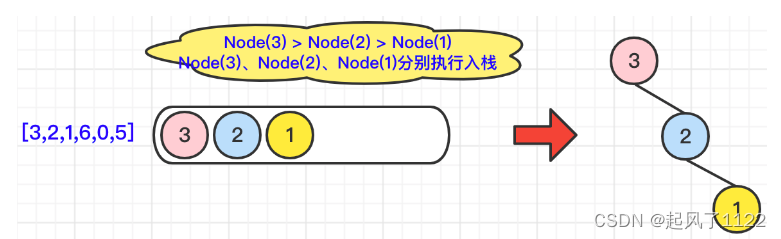
🌻 以nums=[3,2,1,6,0,5]为例，看单调栈如何创建二叉树。

🌿首先，对于数组前3个元素，满足Node(3)>Node(2)>Node(1),所以3个元素直接入栈，并且构造二叉树Node(3).right=Node(2),Node(2).right=Node(1)

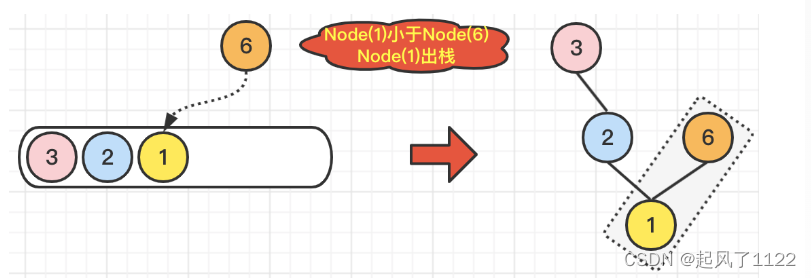
在这里插入图片描述

🌿当遍历到Node(6)时，由于Node(1)<Node(6),所以Node(1)出栈，并且执行Node(6).left=Node(1),又由于Node(2)<Node(6),所以Node(2)也出栈，并且执行Node(6).left=Node(2)，

🔔注意：此时Node(6)的左节点从Node(1)变成了Node(2),由于Node(3)<Node(6),所以Node(6).left=Node(3)，注意：此时Node(6)的左节点从Node(2)变成了Node(3)，由于栈中没有元素可以出栈了，没有可以和Node(6)对比的元素了，因此Node(6)入栈。

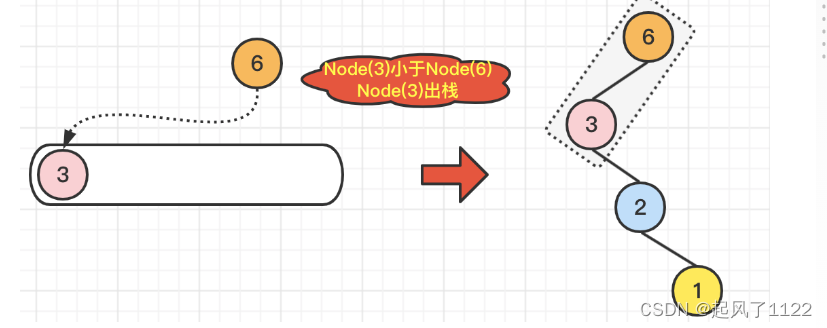
在这里插入图片描述

🌿我们继续遍历到Node(0)，由于Node(0)小于栈顶元素Node(6)，所以Node(0)直接入栈就可以了。但是，别忘记维护一下二叉树，也就是说，配置一下Node(6).right = Node(0)。具体操作，如下图所示：

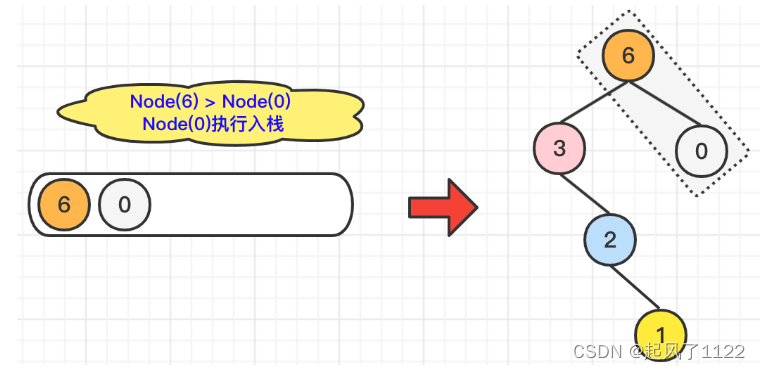
在这里插入图片描述

🌿最后，我们遍历到了Node(5)，由于Node(5)大于当前栈顶元素Node(0)，所以Node(0)执行出栈操作，并维护二叉树结构Node(5).left = Node(0);在对比Node(5)小于当前栈顶元素Node(6)，所以，Node(5)直接入栈即可。维护二叉树结构Node(6).right = Node(5)。具体操作，如下图所示：

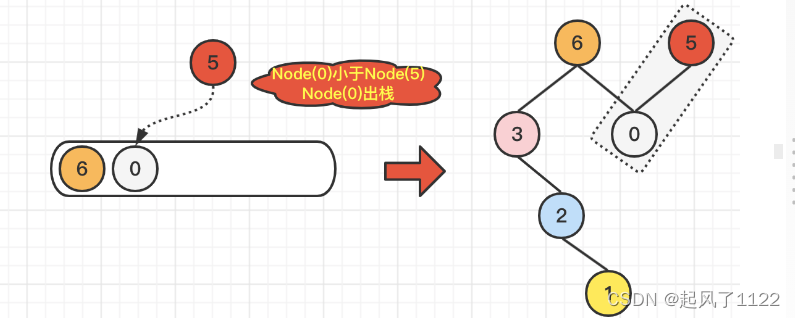
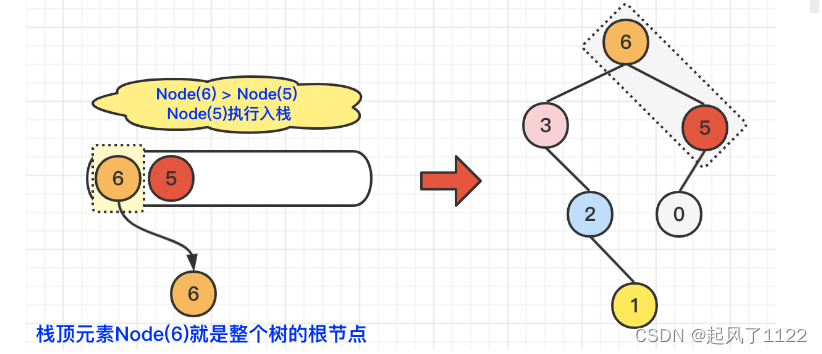
在这里插入图片描述

🌻代码如下：

class Solution {
      public TreeNode constructMaximumBinaryTree(int[] nums) {
          Deque<TreeNode> q=new ArrayDeque<>();
          for(int i=0;i<nums.length;i++){
              TreeNode node=new TreeNode(nums[i]);
              while(!q.isEmpty()){
                  TreeNode topNode=q.peekLast();
                  if(topNode.val>node.val){
                      q.addLast(node);
                      topNode.right=node;
                      break;
                  }else{
                      q.removeLast();
                      node.left=topNode;
                  }

              }
              if(q.isEmpty()){
                  q.addLast(node);
              }

          }
          return q.peek();

    }
}

🌻补充：

`1.单调栈`

🟢单调栈是一种特殊的栈数据结构，它的特点是栈内的元素保持单调递增或单调递减的顺序。具体来说，单调栈可以分为单调递增栈和单调递减栈两种类型。

在使用单调栈时，通常需要解决与元素的大小关系相关的问题，例如找到数组中元素的下一个更大元素、下一个更小元素等。单调栈提供了一种高效的方法来解决这些问题。

🟢单调递增栈的特点是栈内的元素从栈底到栈顶保持递增的顺序，而单调递减栈则是栈内的元素从栈底到栈顶保持递减的顺序。

🟢使用单调栈的好处包括：

快速找到某个元素的下一个更大或更小元素。通过保持栈内元素的单调性，可以在 O(1) 的时间复杂度内找到下一个更大或更小的元素，而无需遍历整个数组或其他数据结构。
节省空间和时间复杂度。相比其他数据结构，单调栈通常可以以更少的空间和更低的时间复杂度来解决一些特定的问题。解决一些特定的问题。单调栈常用于解决与元素大小相关的问题，如找到数组中元素的下一个更大元素、下一个更小元素，或者计算数组中每个元素的距离最近的更大或更小元素等。