BAPC 2022 Pre 部分题解
- K (11). Lots of Liquid
- 题目描述
- 题意
- 思路
- 代码
- F (6). Fastestest Function
- 题目描述
- 题意
- 思路
- 代码
- B (2). Bubble-bubble Sort
- 题目
- 代码
- A (1). Abbreviated Aliases
- 题目
- 题意
- 思路
- 代码
- I (9). Jabbing Jets
- 题目
- 题意
- 思路
- 代码
- E (5). Extended Braille
- 题目
- 题意
- 思路
- 代码
K (11). Lots of Liquid
题目描述
题目描述
You work at a warehouse that sells chemical products, where somebody just placed an order for all the Boron Acetate Phosphoric Carbonate (BAPC) that you have in store. This liquid is stored in many separate lots, in cube-shaped containers, but your client requires the order to be delivered in a single cubeshaped container that fits all the BAPC liquid perfectly. What should be the size of this container?
输入描述
The input consists of:
One line with an integer n
(1≤n≤105
), the number of cube-shaped containers that you have in store.
One line with n
floating-point numbers c
(1≤c≤109
), the length of one of the sides for each of these containers.
输出描述
Output the length of one of the sides of the cube-shaped container that will contain all the BAPC liquid.
Your answer should have an absolute or relative error of at most 10−6
.
样例
输入 复制
3
21 28 35
输出 复制
42
输入 复制
3
22.10 2022 1337
输出 复制
2200.6131345362505
输入 复制
3
1.41421356 2.718281828 3.1415926535
输出 复制
3.777901284526486
题意
有n个边长不同的液体,正好分别放在一个立方体容器内,如果想把这些液体放在一个大的立方体容器内,问这个立方体边长为多少
思路
将这n个数的立方和相加,最后开立方就行。(注意不要用pow开立方,精度差会很大,用cbrt)
代码
#include <bits/stdc++.h> // include万能头文件
using namespace std;
int main(){
int n; // 定义整型变量n
cin>>n; // 输入n
double ans=0; // 定义双精度浮点数ans并初始化为0
for (int i=1;i<=n;i++){ // 循环n次
double x; // 定义双精度浮点数x
cin>>x; // 输入x
ans+=pow(x,3); // 计算x的3次方并加入ans中
}
ans=cbrt(ans); // 对ans进行立方根运算
printf("%.7lf",ans); // 输出结果,保留小数点后7位
}
F (6). Fastestest Function
题目描述
题目描述
You are working as a software developer for the Bug Acquisition Programming Company. They developed a specific piece of software called Program C that they sell to their clients. For the past weeks, you have been working on optimising a specific function foo in the
main code path in Program C. You have made it a lot faster and would like to show off to your boss about it.
Your IDE has a nice tool that allows you to profile your code and tell you what percentage of the total running time foo takes. You can run this on the version before your change and after your change. However, you think it looks a lot cooler if you can just tell your boss how
much faster you have made foo itself.
输入描述
The input consists of:
One line with two integers x
and y
(0<x,y<100
), where x
is the percentage of the total running time that foo took before optimising and y
the percentage of the total running time it took after optimising.
输出描述
Output the factor of how much faster foo got after your optimization.
Your answer should have an absolute or relative error of at most 10−6
.
样例
输入 复制
75 50
输出 复制
3.0
输入 复制
50 75
输出 复制
0.3333333333333333
输入 复制
50 50
输出 复制
1.0
题意
有一堆数据,C开始花时占总时长比例为X,C经过修改后花时占修改后总时长比例为Y,问开始花的时间/修改后花的时间为多少
思路
C花的时间在改变,但其他的时间为改变,因此我们可以通过修改前后的其他的时间占比变化,来求出修改后花的时间
代码
#include <bits/stdc++.h> // 引入万能头文件
using namespace std;
int main(){
double a1,a2; // 定义双精度浮点数变量a1和a2
cin>>a1>>a2; // 输入两个数,分别存储到变量a1和a2中
double b1=100-a1,b2=100-a2; // 计算a1和a2的补数,分别赋值给变量b1和b2
double bs; // 定义用于存储结果的变量bs
bs=b1/b2; // 计算b1与b2的比值
a2=bs*a2; // 根据比值计算新的a2
bs=a1/a2; // 再次计算a1和a2的比值
printf("%.7lf",bs); // 输出计算结果,保留小数点后7位
}
B (2). Bubble-bubble Sort
题目描述
Bubbles! As a fanatical supporter of the Bubbles Are Perfect Creatures movement, you have accumulated a large collection of bubbles in all colours and sizes. Being a long time member, your bubbles are among the best in the world, and now is the time to show this. Tomorrow, the yearly Bubble Exposition will be held, and your goal is to win the Bubble Prize and become the Bubble Champion!
However, this is not an easy competition. In order to win, you do not only need the most beautiful bubbles, you also need the best-looking placement of bubbles. You have decided to order the bubbles by bubbliness: less bubblier bubbles to the left, more bubblier bubbles to the right. However, it is hard to compare all the bubbles in your collection at once. In fact, you can only compare up to k
bubbles by eye before losing track of all the bubbles. Since your collection consists of more than k
bubbles, you need a fancier sorting algorithm.
Your first thought is to use the best sorting algorithm for bubbly purposes, namely Bubble Sort. However, this is the most prestigious bubble competition, so you decide to do better: Bubble-bubble Sort. It works as follows.
Initially, your bubbles are placed in an arbitrary order. Every hour, you do the following: you look at the first k
bubbles and place them in the optimal order. Then, you look at bubbles 2∼k+1
and place those in the correct order. Then, you look at bubbles 3∼k+2
, and so on, until you have placed the last k
bubbles in the correct order. You then admire how the bubble collection looks so far until the next hour begins and you start at the first bubbles again.
Is this algorithm fast enough to place all your bubbles, or do you need to go further and invent a Bubble-bubble-bubble Sort algorithm? To be precise, after how many hours are the bubbles in the optimal positions?
输入描述
The input consists of:
One line with two integers N,K(2≤K<N≤2500
), the number of bubbles and the number of bubbles you can sort at once.
One line with N
integers a(0≤a≤109
), the bubbliness of each bubble in the initial placement of your bubble collection.
输出描述
Output the number of hours needed to sort your bubble collection.
样例
输入 复制
5 2
3 4 1 5 2
输出 复制
3
输入 复制
8 3
60 8 27 7 68 41 53 44
输出 复制
2
输入 复制
6 3
3 2 4 2 3 1
输出 复制
3
题目
问每一轮从头到尾遍历,遍历的时候每一次都对区间长度为m的序列进行排序,直到序列长度严格从小到大才结束,问有多少轮
代码
#include <bits/stdc++.h> // 引入万能头文件
using namespace std;
int a[2550]; // 定义大小为2550的整型数组a
int main(){
int n,m; // 定义两个整型变量n和m
cin>>n>>m; // 输入n和m的值
for (int i=1;i<=n;i++){ // 循环读入n个数字
cin>>a[i];
}
int ans=0; // 定义整型变量ans,并初始化为0
while (1){ // 循环执行以下操作,直到整个数组为升序为止
int flag=0;
for (int i=1;i<n;i++){ // 判断数组是否已经为升序
if (a[i]>a[i+1]){
flag=1; // 如果存在逆序,则flag置为1
break;
}
}
if (flag==0){ // 如果整个数组已经为升序,则跳出循环
break;
}
for (int i=1;i+m-1<=n;i++){ // 对每m个元素为一组进行排序
sort(a+i,a+i+m);
}
ans++; // 统计排序次数
}
cout<<ans; // 输出排序次数
}
A (1). Abbreviated Aliases
题目
You are the owner of a large successful internet site with lots of users. All these users have chosen an alias of exactly L
characters for logging into the site. Recently, you noticed that you started running into disk space issues: storing all these aliases takes up a lot of data!
You do not have enough money to buy extra storage, so you are looking for ways to reduce the storage space needed. A friend gives you the following compression idea that might help: instead of storing the full alias for each user, you might get away with only storing a prefix of that alias, as long as no other alias has the same prefix. For example, if you just have the aliases james and jacob, you can store only jam and jac and still be able to identify them both.
This idea sounds quite interesting to you, and you are looking forward to finally having more space available on your disk again. You would like to find out how much space you need to store all aliases using this compression technique.
输入描述
The input consists of:
One line with two integers N,L(2≤N≤104,1≤L≤103
),the number of aliases and the length of each alias.
N
lines, each with an alias:a string consisting of exactly L
English lowercase characters(a-z), Each alias is unique.
输出描述
Output the total number of characters you still need to store if you apply this compression technique.
样例
输入 复制
2 5
james
jacob
输出 复制
6
输入 复制
4 4
xxxx
yxxx
xxyx
yxxy
输出 复制
14
题意
求几个字符串最短不同子字符串的总长度
思路
先对给出的字符串进行排序,然后通过和前一个,后一个字符串的比较,找到最大不同字符串的长度,但需要对第一个和第n个做特殊处理
代码
#include <bits/stdc++.h> // 引入万能头文件
using namespace std;
string s[10005]; // 定义大小为10005的字符串型数组s
int main(){
int n,m; // 定义两个整型变量n和m
cin>>n>>m; // 输入n和m的值
for (int i=1;i<=n;i++){ // 循环读入n个字符串
cin>>s[i];
}
sort(1+s,1+s+n); // 对字符串数组进行排序
int ans=0; // 定义整型变量ans,并初始化为0
for (int i=1;i<=n;i++){ // 循环计算总代价
int cnt1=0,cnt2=0;
if (i==1){ // 如果当前字符串是第一个字符串
for (int j=0;j<m;j++){ // 判断它与第二个字符串之间的不同字符数
if (s[i][j]!=s[i+1][j]){
ans+=j+1;
break;
}
}
}else if (i==n){ // 如果当前字符串是最后一个字符串
for (int j=0;j<m;j++){ // 判断它与倒数第二个字符串之间的不同字符数
if (s[i][j]!=s[i-1][j]){
ans+=j+1;
break;
}
}
}else{ // 如果当前字符串不是第一个也不是最后一个
for (int j=0;j<m;j++){ // 计算它与下一个字符串之间的不同字符数
if (s[i][j]!=s[i+1][j]){
cnt1=j+1;
break;
}
}
for (int j=0;j<m;j++){ // 计算它与上一个字符串之间的不同字符数
if (s[i][j]!=s[i-1][j]){
cnt2=j+1;
break;
}
}
ans+=max(cnt1,cnt2); // 将这两个计数器中的最大值累加到总代价中
}
}
cout<<ans; // 输出总代价
}
I (9). Jabbing Jets
题目
You have just gotten a new job at the Bathroom Accessories Production Company. The first task you are given is to jab holes into showerheads. To prove yourself, you have decided you want to create as many holes as possible.
However, you cannot just randomly drill holes everywhere in the showerhead. (At least, not without getting fired.) In order to ensure that the showerheads look aesthetically pleasing, the company has composed some guidelines which you will have to follow. See Figure J.1 for some examples of aesthetically pleasing showerheads.
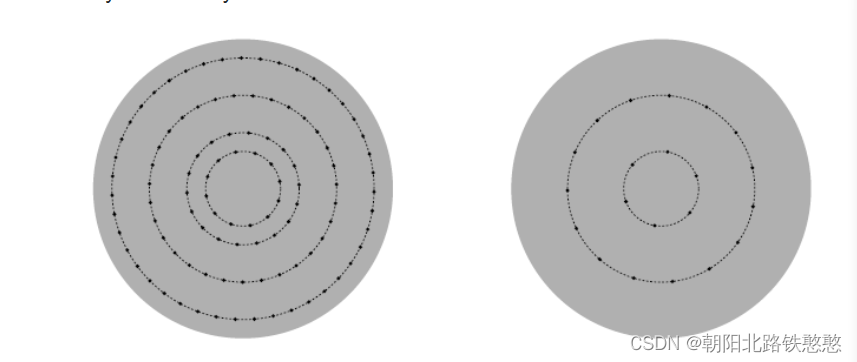
-
The holes should be arranged in concentric circles of radii r1,r2,…,rn
-
the center of every hole should be on one of these circles.
The distance between the centers of any two holes should be at least e
.
How many holes can you make at most?
输入描述
The input consists of:
One line with two integers n
and e
(1≤n,e≤104
), the number of circles and the minimal distance between holes.
One line with n
integers r1,…,rn
(1≤ri≤104
), the radii of the circles.
It is guaranteed that the numbers ri
are given in increasing order, and that ri+1−ri≥e
. Furthermore, it is guaranteed that increasing any radius ri
by at most 10−6
will not change the final answer.
输出描述
Output the maximal number of holes that you can make in the showerhead.
样例
输入 复制
4 1
2 3 5 7
输出 复制
104
输入 复制
2 2
2 5
输出 复制
21
输入 复制
3 20
14 53 80
输出 复制
44
题意
求半径为r的圆上,能打多少个直线距离为m的点
思路
知道弦长和半径通过余弦定理可以求出该弦对应的余弦值,再通过对这个余弦值求反函数得到角度,然后在看能打多少点(注意:至少能打一个点,以及精度误差所以得加上一个1e-6)
代码
#include <bits/stdc++.h> // 引入万能头文件
using namespace std;
const double pai=acos(-1.0); // 定义常量pai,并赋值为acos(-1.0)
int main(){
double n,m; // 定义两个双精度浮点数n和m
cin>>n>>m; // 输入n和m的值
long long ans=0; // 定义长整型变量ans,并初始化为0
for (int i=1;i<=n;i++){ // 循环读入 n 个数字
double x;
cin>>x;
if (2*x<m){ // 判断是否只需放置一个正方形就可将当前数字覆盖
ans+=1;
continue;
}
double c=(x*x+x*x-m*m)/(2*x*x); // 计算正方形角度
c=acos(c);
double ds=(2*pai/c+1e-6); // 求当前数字需要覆盖的正方形数量
ans+=(long long)ds;
}
cout<<ans; // 输出覆盖数字所需正方形的总数
}
E (5). Extended Braille
题目
题目描述
The Blind Association for Pretty Calligraphy is annoyed by the lack of emoticons and math symbols in the braille alphabet. Given that the braille alphabet is supported by the Unicode format, it only makes sense to make all Unicode characters supported in braille.
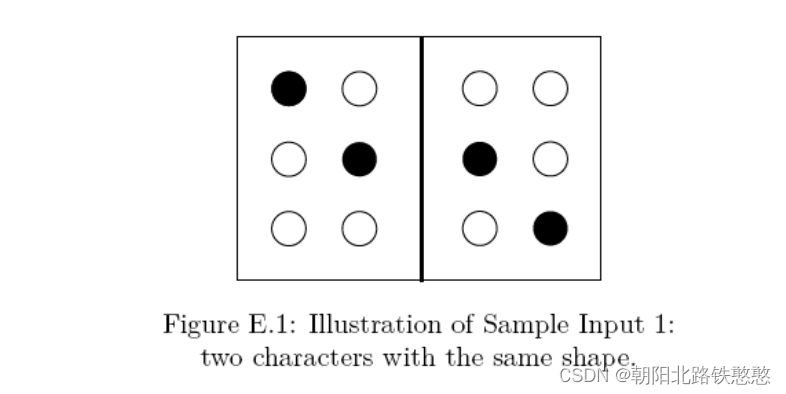
The goal is to extend the braille alphabet to include all Unicode characters. Of course, this will not fit in the standard 2×3
format, so using a bigger box is allowed. Important is that no two braille characters are the same up to translation, i.e., have the same shape. See Figure E.1 for an example. You let a designer make up a large braille alphabet, and your job is to check how many unique shapes there are among the characters.
输入描述
The input consists of:
One line with an integer n
(1≤n≤105
), the number of braille characters.
Then for each of the n
braille characters:
One line with an integer m
(1≤m≤1000
), the number of dots.
m
lines, each with two integers x
and y
(|x|,|y|≤1000
), the coordinates of the dots.
The total number of dots is at most 106
.
输出描述
Output the number of distinct braille characters up to translation.
样例
输入 复制
2
2
0 2
1 1
2
0 1
1 0
输出 复制
1
输入 复制
2
3
-1 0
0 1
1 0
3
-1 0
0 -1
1 0
输出 复制
2
题意
相当于给了n张白纸,每张白纸上有m个黑点,求不同的图案数
思路
对每张白纸上的点排序,以第一张图的第一个点为标准,然后计算以后每一张图的第一个点与其的差,然后将点的坐标规范到一起
代码
#include <bits/stdc++.h>
using namespace std;
typedef pair<int,int> p;
vector<pair<int,int>> v[100005];
set<vector<pair<int,int>>> st;
bool cmp(p x,p y){
if (x.first==y.first){
return x.second<y.second;
}else{
return x.first<y.first;
}
}
int main(){
int t;
cin>>t;
int n,x,y;
for (int i=0;i<t;i++){
cin>>n;
for (int j=0;j<n;j++){
cin>>x>>y;
v[i].push_back({x,y});
}
sort(v[i].begin(),v[i].end(),cmp);
}
st.insert(v[0]);
int k,m;
for (int i=1;i<t;i++){
k=v[0][0].first-v[i][0].first;
m=v[0][0].second-v[i][0].second;
for (int j=0;j<v[i].size();j++){
v[i][j].first+=k;
v[i][j].second+=m;
}
st.insert(v[i]);
}
cout<<st.size();
}