目录
3.1.1 引子(顺序查找)
什么是树
查找
3.1.2 引子 二分查找例子(BinarySearch)
二分查找
3.1.3 引子 二分查找实现
二分查找代码
二分查找的启示
3.1.4 树的定义
一些基本术语:
3.1.5 树的表示
3.1.1 引子(顺序查找)
什么是树
在客观世界上许多事物存在层次关系。如人类社会的家谱、社会组织管理结构、省市县乡镇的分级,计算机中为了还原这种结构,使用了树这种数据结构。
那么为什么要使用这种层次结构?因为分层组织在数据管理方面有更高的效率
下面以数据管理的基本操作之一:查找为例来分析,如何实现有效的查找?
查找
实质:根据某个给定的关键词K,从集合R中找出与关键词K相同的数据
1. 静态查找
- 定义:集合中的数据是固定的。没有插入和删除,对数据集的操作只有查找。——比如一本出版字典
- 实现:一般使用数组存放数据
- 方法:顺序查找
2. 动态查找
- 定义:集合中数据是动态变化的。对数据集的操作有查找、插入和删除。——比如一个论文数据库
顺序查找详解:(实际上就是遍历)时间复杂度:O(n)
typedef struct LNode *List;
struct LNode{
ElementType Element[MaxSize];
int length;
};
int SequentialSearch(List Tbl,ElementType K)
{//遍历ElementType查找关键字为K的数据元素
int i;
Tbl->Element[0] = K;//建立哨兵,预先设立边界值而不需要每次都判断
for(i = Tbl->Length; Tbl->Element[i] != K; i--);
//查找成功返回下标,不成功返回0
return i;
}
//不用哨兵的
int SequentialSearch(List Tbl,ElementType K)
{
int i;
//两个退循环条件,i控制边界,tbl检测是否相等
for(i = Tbl->Length; i>0 && Tbl->Element[i] != K; i--);
return i;
}3.1.2 引子 二分查找例子(BinarySearch)
假设两个地点AB之间的高压电站有100w个,从A向B输电,某一天两个地方都突然停电了,现在需要排查是哪里的电站出问题。如果一个一个排查过去,平均需要50w次才能排查结束。如果先从最中央的一个电站开始排查,再向断电的那一半的中间...每次折半查找,那么只需要log2(1000000)=20次就可以排查完毕。
二分查找
- 前提:数据元素的关键字需要是有序且连续存放
- 退出条件:1.初始时right>left,结束时left>right,二者错位,说明查找失败2.查找成功,返回
3.1.3 引子 二分查找实现
二分查找代码
//函数参数表为存放着数据的列表Tbl和要找的元素K
int BinarySearch(List Tbl, ElementType K)
{
//定义左中右标识变量,赋初值,-1为方便返回NoFound
int left,right,mid,NoFound = -1;
//初始左右边界,先让左边界为最左侧元素,右边界为表尾
left = 1;
right = Tbl->length;
while(left <= right)
{
mid = (left + right)/2;
//若中值大于要找的元素K
if(K < Tbl->Element[mid]){
right = mid - 1;//说明应该往左半侧找,把右边界更新为此时的中值-1即可
}else if(K > Tbl->Element[mid]){
left = mid + 1;
}else{
return mid;
}
}
//如果找到了会提前退出循环,没找到会返回NoFound即-1
return NoFound;
}这个算法的时间复杂度是对数级的O(logN)
二分查找的启示
由二分查找判断元素的顺序可以绘制出如下判定树
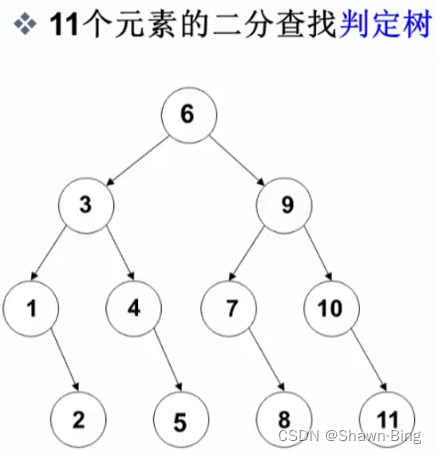
从图中可以发现:
- 每个结点需要查找的次数刚好等于这个结点所在的层数
- 查找次数的上限是这个判定树的深度
- 如果有n个结点,那么判定树的深度为[log2(N)]+1
- 平均查找次数ASL = (每层个数*层数之和)/总结点数。此树ASL = (1+2*2+4*3+4*4)/11=3
那么如果直接将数据存储成树这样的形式,会不会对数据的查找更有裨益呢?当然会。之后我们就将讲到查找树这种存储形式。
3.1.4 树的定义
树(Tree):n(n>=0)个结点构成的有限集合
空树:n=0,即没有结点。其对应的是非空树。
对于任意一颗非空树,它具备以下性质:
树中有一个称为根(Root)的特殊结点,用r表示
其余结点可分为m(m>0)个互不相交的有限集T1、T2、...、Tm,其中每个集合本身也是一棵树,称为原来树的子树(SubTree)
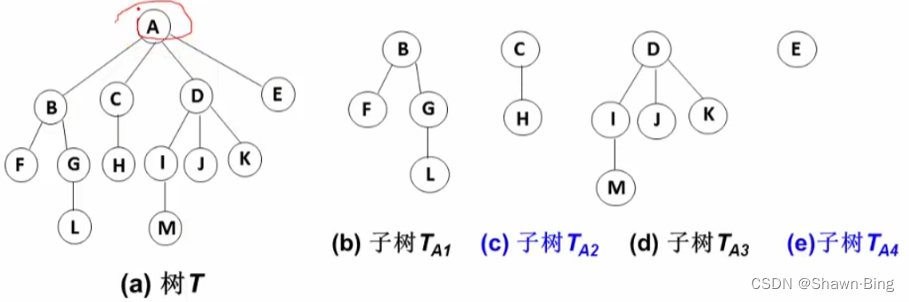
非树:
- 子树之间有相交
树:—— 一种保证结点联通方式最小的连接方式
- 子树之间不能相交
- 除根结点以外,每个结点有且仅有一个父结点
- 一颗N个结点的树有N-1条边
一些基本术语:
- 结点的度:结点子树个数(有几个直接相连的子结点)
- 树的度:树的所有结点中最大的度数(树所有结点里子树最多的那一项,子树的个数)
- 叶结点(Leaf):度为0的结点
- 父结点(Parent):有子树的结点是其子树的根节点的父结点
- 子结点(Child):也称孩子节点。若A结点是B结点的父结点,则称B结点是A结点的子结点。
- 兄弟结点(Sibiling):具有同一父结点的各结点彼此是兄弟结点
- 路径和路径长度:从结点n1到nk的路径为一个结点序列n1,n2,...,nk,ni是ni+1的父结点。路径所包含边的个数为路径的长度。
- 祖先结点(Ancestor):沿树根到某一结点路径上所有结点都是这个结点的祖先结点。(层数高的是层数低的祖先)
- 子孙结点(Descendant):某一结点的子树中的所有结点是这个结点的子孙
- 结点的层次(Level):规定根结点在一层,其它任一结点的层数是其父结点层数+1
- 树的深度(Depth):树中所有结点中的最大层次是这棵树的深度
3.1.5 树的表示
知道了树的抽象结构和基本概念,下面我们需要能在计算机中表示树这种结构。首先我们肯定是需要在已有的结构中选择一种。
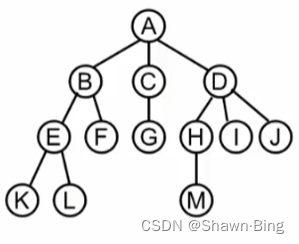
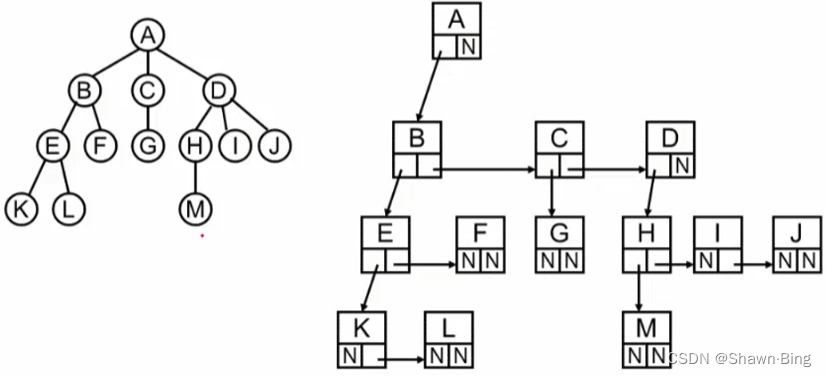
使用结构+链表
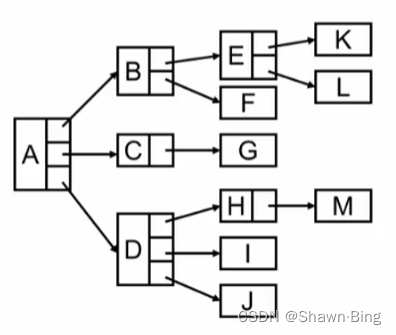
看似结构很像,实则在实现过程中,每个结点指向其他结点的个数并不相同,结构不一定能囊括所有情况。那如果将所有的结点都设计成一个形式,比如都留3个指针域,有的结点可能只用一个,但这样能保证结点结构统一,处理方便。但当树的体积非常庞大时候,这样的做法会造成巨大的浪费。
有一种较好的表示方法,同样是使用结构+链表的形式,所有结点结构相同。每个结点包含两个指针域,一个是FirstChild,指向这个结点的第一个孩子结点,另一个是NextSibiling,指向它的下一个兄弟结点。这种形式的树我们称为:二叉树(链表)