结合自由能计算

打分函数

背景

打分函数广泛应用于基于结构的计算辅助药物设计，其通过定量化评估药-靶的相互作用为药物研发中的药效评估提供理论依据，提高活性化合物甄别的效率。定量评估药物与靶标蛋白的相互作用通常分为两步，一步是对接处理（docking process），主要指构象搜索，找出潜在的binding pose；另一步是打分处理（scoring process），通常指打分，预测药-靶结合力。大部分打分函数并不基于完整的物理模型而作近似处理，因此往往不严格遵循多体扩展理论，守恒定律，对称不变性等，甚至有些基于知识的打分函数的表达式完全不含物理意义。事实上，作为应用于药物高通量筛选场景下的一种工具，大部分打分函数以效率为中心，通过近似的手段追求精度与效率的平衡。

打分函数分类

从上世纪的90年代起，已报道的打分函数已经有超过一百种。先前已有一些工作综述过打分函数的分类，比如将打分函数分为基于力场的，基于经验的，基于知识的三种类型。近年来随着这个领域的研究不断深化，一些新的技术比如机器学习的引入带来的描述符的引入，加上基于经验的打分函数的表达式与基于力场的表达式的相似性，原有的打分函数分类描述会让初涉此领域的研究人员感到迷惑，因此王任小课题组在2015年结合打分函数研究的进展，对打分函数做出了新的分类的阐述[6]。其将打分函数大致进行了以下四类的阐述：分别是基于物理（力场）的打分函数，基于经验（回归）的打分函数，基于平均力势（知识）的打分函数，基于描述符（机器学习）的打分函数。

炼金术自由能计算方法（AFEM）

炼金术自由能计算的定义特征：利用一系列修改的势能函数$U(x;\lambda )$来做模拟。其中，参数入可以调控在真实化学体系中不会出现的相互作用。用一个或者多个模拟来收集所有热力学态的能量以计算初态$({\lambda }_0)$和末态（${\lambda }_1$）之间的自由能差：

$$\Delta f\equiv f\left({\lambda }_1\right)-f\left({\lambda }_0\right)=-\ln \frac{Z\left({\lambda }_1\right)}{Z\left({\lambda }_0\right)}$$

适用性如何
当需要（缓慢或昂贵的）合成才能进行实验或实验成本过高时，自由能计算才有吸引力。而且自由能计算可以给出实验难以得到的答案。
准确度是否足够
如果是为了在合成许多化合物时优化先导化合物，那么即使在1-2kcal/mol的范围内精确地计算自由能也是很有吸引力的。
成本如何
关于“成本”，与实验相比，不仅指的是计算所产生的花费成本，还有时间成本，即计算是否快于实验。
是否需要探索性研究
如果不确定所研究项目是否可行，一个可能的选择是先进行一个简短的探索性严究，以评估为数不多的配体的可行性。这足以初步了解所提出目标计算的可行性和准确性。

溶剂化自由能的意义

自由能是最重要的热力学性质之一，一个物理、化学过程的自由能变化可以帮助我们了解平衡状态下该过程自发进行的程度。根据ben-Naim定义，溶剂化过程是在恒温恒压下，溶质分子在固定位置从理想气体状态下进入到液相的过程若溶剂为水，则该过程被称为水合过程。溶剂化过程的自由能变化即为溶剂化自由能，它描述的是溶质分子在溶剂中溶解的难易程度。溶剂化自由能与诸多热力学性质相关，可以用于计算配分系数、溶解度、结合或解离常数（结合自由能、酸碱解离常数）等，计算溶剂化自由能能够帮助我们理解和处理诸多环境问题，改善药物溶解性而提高药效、减小其负作用等。

MMPBSA

$$\left(\Delta G_{Solv,Rec}+\Delta G_{Solv,Lig}\right)+\Delta G_{Solv,\text{ bind }}=\Delta G_{Gas,\text{ bind }}+\Delta G_{Solv,\text{ Comp }}$$

进入液相中时溶剂化能的变化; $\Delta G_{Solv,bind}$ 和 $\Delta G_{Gas,\text{ bind }}$ 分别为液相中和气相 中的结合自由能。上式变形即可得结合自由能的公式:
$$\Delta G_{\text{Solv,bind }}=\Delta G_{Gas,\text{ bind }}+\Delta G_{Solv,Comp}-\left(\Delta G_{Solv,Rec}+\Delta G_{Solv,Lig}\right)$$

通过该热力学循环可以巧妙地避开液态环境中复杂的能量变化，使得生物大分子体系中的结合自由能的计算变得可行且简便，这也正是MM/PB(GB)SA的优势所在。

结合自由能用吉布斯自由能方式表达可得：
$$\Delta G_{\text{solv,bind }}=\Delta H-T\Delta S$$
$\text{ 上式种焓变 }(\Delta H)\text{ 为气相能 }\left(\Delta E_{MM}\right)\text{ 和溶剂化能 }\left(\Delta G_{sol}\right)\text{ 之和: }$
$$\Delta H=\Delta E_{MM}+\Delta G_{sol}$$

$\text{ 式中, 气相能 }\left(\Delta E_{MM}\right)\text{ 可被分解成如下: }$
$$\Delta E_{MM}=\Delta E_{\text{ele }}+\Delta E_{vdW}+\Delta E_{int}$$

其中 $\Delta E_{ele}、\Delta E_{vdW}$ 和 $\Delta E_{int}$ 分别代表静电项、范德华项和内能项。 $\Delta E_{int}$ 内能由键能、 键角能和二面角能。 $\Delta G_{sol}$ 是极性溶剂化能 $\left(\Delta G_{pb}\right)$ 和非极性溶剂化能 $\left(\Delta G_{np}\right)$ 之 和:
$$\Delta G_{sol}=\Delta G_{pb}+\Delta G_{np}$$
上式中 $\Delta G_{pb}$ 是使用AMBER软件中PBSA程序通过求解线性化泊松-波尔兹曼方程 得到; 非极性溶剂化能由溶剂可及表面积 (SASA) 使用如下公式计算
$$\Delta G_{np}=\gamma \cdot \mathrm{SASA}+\beta$$

泊松-玻尔兹曼模型（PB model）

• 溶质作为实体, 介电常数较低 (2-4)
• 溶剂作为连续介质, 介电常数较高 (80) 介电常数非常数的泊松方程为
  介电常数非常数的泊松方程为
  $$\nabla \cdot [\epsilon (\mathbf{r})\nabla \varphi (\mathbf{r})]=-4\pi \rho (\mathbf{r})$$
• 通过玻尔兹曼分布考虑到离子的存在
  线性的泊松-玻尔兹曼方程为
  $$\nabla \cdot [\epsilon (\mathbf{r})\nabla \varphi (\mathbf{r})]-\epsilon (\mathbf{r}){\kappa }^2\varphi (\mathbf{r})=-4\pi \rho (\mathbf{r})$$
• 通过一个数值网格上的有限差分方法解PB方程
  PB溶剂化自由能：
  $$\Delta G_{\text{elec }}=\frac{1}{2}\sum q_i\left[{\varphi }_{\epsilon =80}\left({\mathbf{r}}_i\right)-{\varphi }_{\epsilon =80}\left({\mathbf{r}}_i\right)\right]$$

广义波恩模型（GB model）

总的静电能是库伦作用能与在相对介电常数为=的溶剂的波恩自由能之和
$$\begin{array}{rl}\Delta G_{\text{elec }}& =-\left(1-\frac{1}{\epsilon }\right)\sum _{i<j}\frac{q_i{q}_j}{r_{ij}}-\frac{1}{2}\left(1-\frac{1}{\epsilon }\right)\sum _i\frac{q_i^2}{a_i}\\ & =-\frac{1}{2}\left(1-\frac{1}{\epsilon }\right)\sum _{i,j}\frac{q_i{q}_j}{f\left(r_{ij},a_{ij}\right)}\end{array}$$

$\text{ 不同的 GB模型对于 }\mathrm{f}\left(r_{ij},r_{ij}\right)\text{ 和半径 }{a}_{ij}=\sqrt{a_i{a}_j}\text{ 的定义不同 }$
$$f_{ij}\left(r_{ij}\right)=\sqrt{r_{ij}^2+a_{ij}^2\exp \left(-\frac{r_{ij}^2}{4a_{ij}^2}\right)}{a}_{ij}=\sqrt{a_i{a}_j}$$

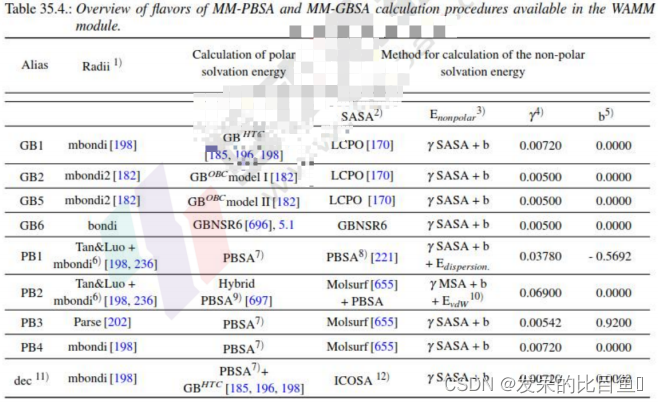
GBSA方法是通过广义Born模型计算极性溶剂化能，在amber中有如下GB模型：