动态规划之背包模型

news2024/10/6 1:39:11

文章目录

    • 采药（01背包）
    • 装箱问题（01背包）
    • 宠物小精灵之收服(二维费用01背包👍😘)
    • 数字组合(01背包)
    • 买书（完全背包）
    • 货币系统（完全背包）

采药（01背包）

✍
在这里插入图片描述
典型01背包模板题

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;

public class Main{
	static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
	static int N = (int) (2e5 + 10);
	static int[][] dp = new int[110][1100]; //最长不上升子序列
	static int k = 0, n = 0;
	static int[] t = new int[N];
	static int[] val = new int[N];
	static int cnt = 0;
	static int time = 0;
	public static void main(String[] args) throws Exception{
		String[] tm = br.readLine().split(" ");
		time = Integer.parseInt(tm[0]);
		n = Integer.parseInt(tm[1]);
		for(int i = 1; i <= n; i++) {
			String[] tv = br.readLine().split(" ");
			t[i] = Integer.parseInt(tv[0]);
			val[i] = Integer.parseInt(tv[1]);
		}
		for(int i = 1; i <= n; i++) {
			for(int j = 0; j <= time; j++) {
				if(t[i] > j) {
					dp[i][j]  = dp[i - 1][j];
				}else {
					dp[i][j] = Math.max(dp[i - 1][j],dp[i - 1][j - t[i]] +val[i]);
				}
			}
		}
		
		System.out.println(dp[n][time]);
	}
}

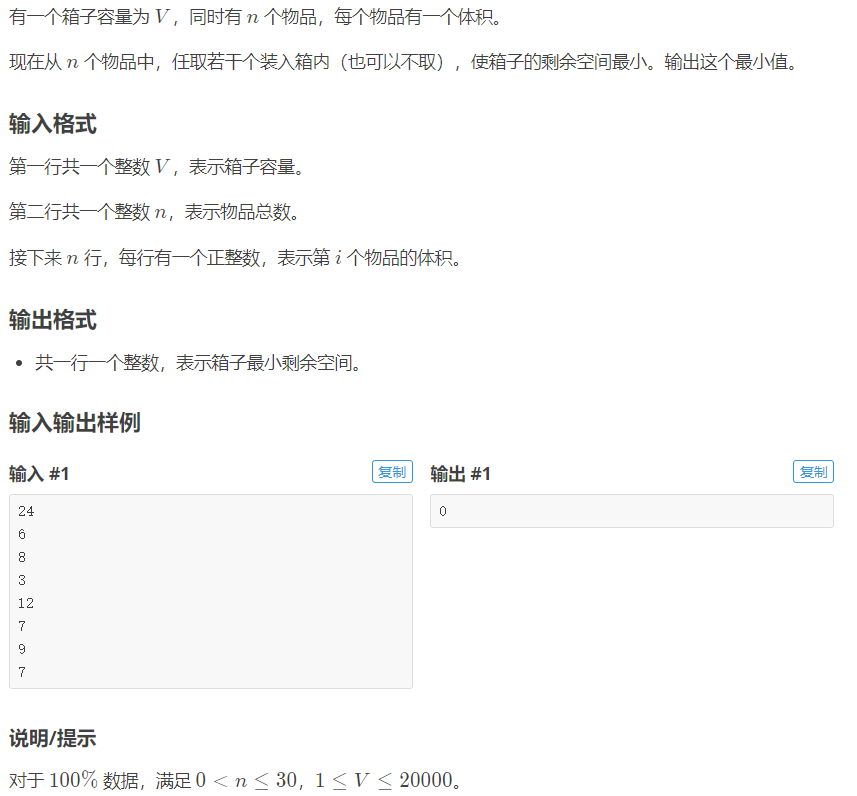
装箱问题（01背包）

✍
在这里插入图片描述
本题可以从两个方向去思考：

法一：
给定n个物品，及每个物品对应的体积，要让剩余空间最少，就是求放进去的体积的体积的最大值。我们将每个物品的体积当作背包的价值，不就等价于之前的求背包的最大价值了。
最后用总的体积-dp[n][vv]

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;

public class Main{
	static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
	static int[][] dp = new int[100][21000];
	static int[] v = new int[21000];
	static int n = 0,vv = 0;
	static long ans = 0;
	public static void main(String[] args) throws Exception{
		vv = Integer.parseInt(br.readLine());
		n = Integer.parseInt(br.readLine());
		for(int i = 1; i <= n; i++) {
			v[i] = Integer.parseInt(br.readLine());
		}
//
//		for(int j = 0; j <= vv; j++) {
//			dp[0][j] = j;
//		}

		for(int i = 1; i <= n; i++) {
			for(int j = 0; j <= vv; j++) {
				dp[i][j] = dp[i - 1][j];
				if(j >= v[i]) {
					dp[i][j] = Math.max(dp[i][j],dp[i - 1][j - v[i]] + v[i]);
				}
			}
		}
		System.out.println(vv - dp[n][vv]);
	}
}

法2：
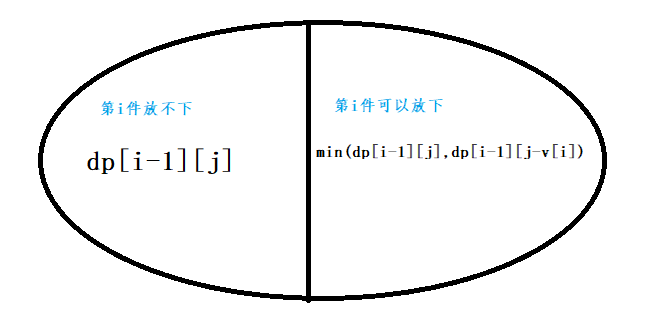
直接设dp[i][j]代表前i个物品，体积为j的最少剩余空间。
初始化dp[0][j]代表前0件物品，体积为j，那么它的最少剩余空间就是j,初始化这些状态。
然后进行转移
在这里插入图片描述

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;

public class Main{
	static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
	static int[][] dp = new int[100][21000];
	static int[] v = new int[21000];
	static int n = 0,vv = 0;
	static long ans = 0;
	public static void main(String[] args) throws Exception{
		vv = Integer.parseInt(br.readLine());
		n = Integer.parseInt(br.readLine());
		for(int i = 1; i <= n; i++) {
			v[i] = Integer.parseInt(br.readLine());
		}

		for(int j = 0; j <= vv; j++) {
			dp[0][j] = j;
		}

		for(int i = 1; i <= n; i++) {
			for(int j = 0; j <= vv; j++) {
				dp[i][j] = dp[i - 1][j];
				if(j >= v[i]) {
					dp[i][j] = Math.min(dp[i][j],dp[i - 1][j - v[i]]);
				}
			}
		}
		System.out.println(dp[n][vv]);
	}
}

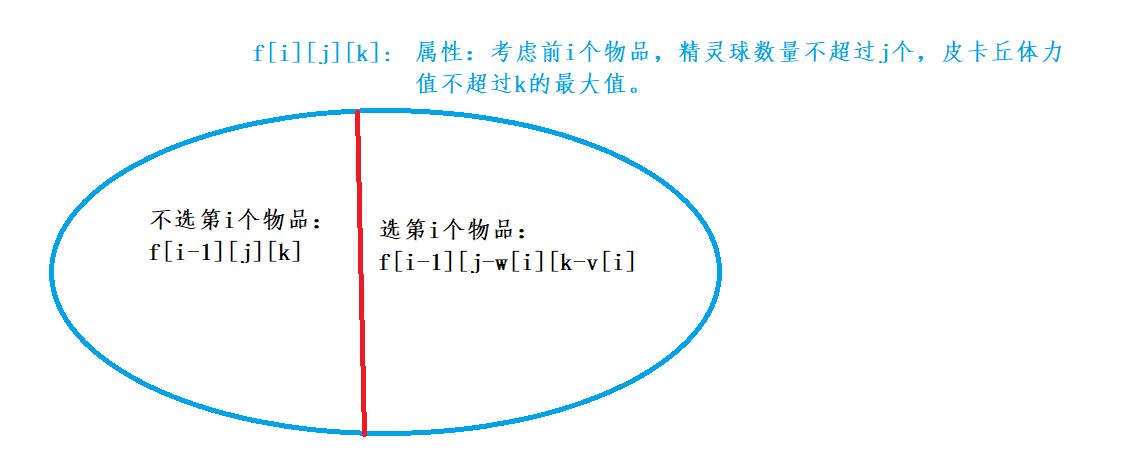
宠物小精灵之收服(二维费用01背包👍😘)

✍
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

本题是01背包的拓展版-二维费用背包
与平时的01背包（一维费用背包的不同是多了一维代价）
一维费用背包我们一般只考虑背包体积是否放的下。
二维费用背包是：同时考虑了背包容积与背包承重。
针对于这个题目：
在这里插入图片描述
本题的两个花费分别是：
精灵球的数量和皮卡丘体力值
而获得的价值就是野生小精灵的数量，需要注意的是，匹拉丘的体力值不能为0，所以皮卡丘的体力值的范围为0-m-1，最后在找一个消耗体力值最小的即可。
需要注意的是，本题必须使用滚动数组优化掉一层，否则会MLE。

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;

public class Main{
	static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
	static int[][] dp = new int[1100][510];
	static int[] v = new int[110]; //伤害
	static int[] w = new int[110]; //数量
	static int n = 0,m = 0,k = 0,num = 0;
	static long ans = 0;
	//dp[i][j][k]只考虑前i个，精灵球数量不超过j，皮卡丘体力值不超过k的最大值
	public static void main(String[] args) throws Exception{
		String[] nmk = br.readLine().split(" ");
		n = Integer.parseInt(nmk[0]); //精灵球数量
		m = Integer.parseInt(nmk[1]); //皮卡丘体力值
		num = Integer.parseInt(nmk[2]); //野生小精灵的数量
		
		for(int i = 1; i <= num; i++) {
			String[] wv = br.readLine().split(" ");
			w[i] = Integer.parseInt(wv[0]); 
			v[i] = Integer.parseInt(wv[1]);
		}
		
		for(int i = 1; i <= num; i++) {
			for(int j = n; j >= w[i]; j --) {
				for(int k = m - 1; k >= v[i]; k--) {
					dp[j][k] = Math.max(dp[j][k],dp[j - w[i]][k - v[i]] + 1);
				}
			}
		}
	
		int s = m;
		while(s > 0 && dp[n][m-1] == dp[n][s - 1]) {
			s--;
		}
		System.out.println(dp[n][m - 1] + " " + (m - s));
	}
}

数字组合(01背包)

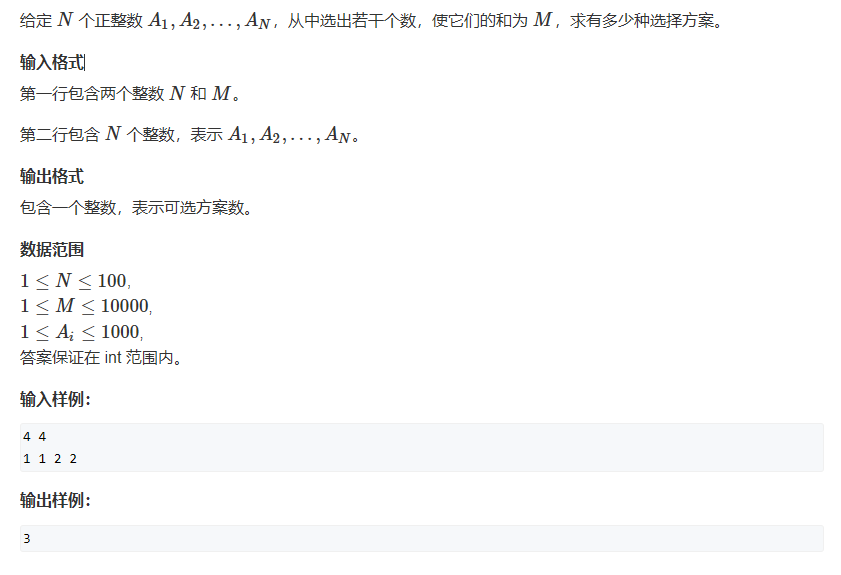
在这里插入图片描述
首相可以想到枚举所有数字的选不选的情况，然后判断是否可行，但是肯定是过不了的，时间复杂度太高了。
每个数字都有选不选，那不就和每个物品都可以放入或者不放入背包差不多嘛，所以可以采用01背包进行求解。
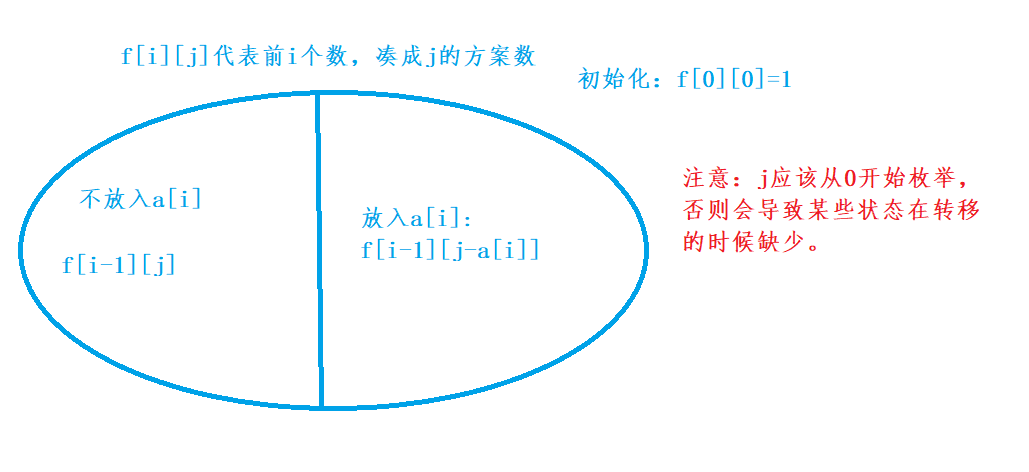
在这里插入图片描述


public class Main{
	static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
	static int N = 110;
	static int M = 11000;
	static int[][] dp = new int[N][M];
	//前i个数 构成m的方案数
	static int n = 0, m = 0;
	static int[] a= new int[N];
	public static void main(String[] args) throws IOException {
		String[] nm = br.readLine().split(" ");
		n = Integer.parseInt(nm[0]);
		m = Integer.parseInt(nm[1]);
		String[] aa = br.readLine().split(" ");
		for(int i = 1; i <= n; i++) {
			a[i] = Integer.parseInt(aa[i - 1]);
		}
		dp[0][0] = 1;
 		for(int i = 1; i <= n; i++) {
			for(int j = 0; j <= m; j++) {
				dp[i][j] += dp[i - 1][j];
				if(a[i] <= j) {
					dp[i][j] += dp[i - 1][j - a[i]];
				}
			}
		}
		System.out.println(dp[n][m]);
	}
}

买书（完全背包）

✍
在这里插入图片描述
因为每本书可以买多本，不需要考虑书本数量的限制，我们只需要考虑钱就行，所以是完全背包。
❗：一定要注意v那一维一定要从0开始，要不会导致有些状态转换不过来。

public class Main{
	static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
	static int M = 1100;
	static int[] v = {0,10,20,50,100};
	static int[][] dp = new int[5][M];
	static int n = 0, m = 0;
	public static void main(String[] args) throws IOException {
		n = Integer.parseInt(br.readLine());
		dp[0][0] = 1; 
		for(int i = 1; i <= 4; i++) { //书
			for(int j = 0; j <= n; j++) { //money
				for(int k = 0; k <= j / v[i]; k++) { //num
					dp[i][j] += dp[i - 1][j - v[i]*k];
				}
			}
		}
		System.out.println(dp[4][n]); 
	}
}

优化版本完全背包：

public class Main{
	static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
	static int M = 1100;
	static int[] v = {0,10,20,50,100};
	static int[] dp = new int[M];
	static int n = 0, m = 0;
	public static void main(String[] args) throws IOException {
		n = Integer.parseInt(br.readLine());
		dp[0] = 1; 
		for(int i = 1; i <= 4; i++) { //书
			for(int j = v[i]; j <= n; j++) { //money
				dp[j] += dp[j - v[i]];
			}
		}
		System.out.println(dp[n]); 
	}
}

货币系统（完全背包）

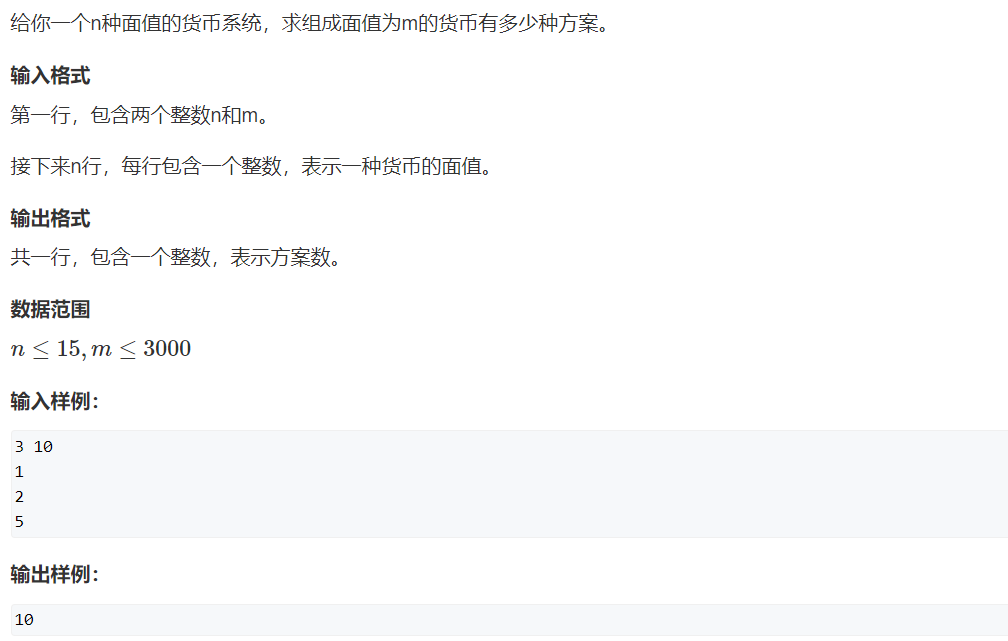
在这里插入图片描述
和上一题基本相同，需要注意数据范围，我们需要开long

public class Main{
	static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
	static int M = 3100;
	static int[] v = new int[20];
	static long[] dp = new long[M];
	static int n = 0, m = 0;
	public static void main(String[] args) throws IOException {
		String[] nm = br.readLine().split(" ");
		n = Integer.parseInt(nm[0]);
		m = Integer.parseInt(nm[1]);
		for(int i = 1; i <= n; i++) {
			v[i] = Integer.parseInt(br.readLine());
		}
		dp[0] = 1;
		for(int i = 1; i <= n; i++) {
			for(int j = v[i]; j <= m; j++) {
				dp[j] += dp[j - v[i]];
			}
		}
		System.out.println(dp[m]); 
		
	}
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/537111.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

ROS：yaml文件解析：base_local_planner、global_costmap、local_costmap、base_local_planner

ROS：yaml文件解析：base_local_planner、global_costmap、local_costmap、base_local_planner

一.costmap_common_params.yaml # 设置了代价地图中障碍物信息的阀值 # obstacle_range&#xff1a;确定了最大范围传感器读数&#xff0c;这将导致障碍物被放入代价地图中。 # 此处设置为2.5m&#xff0c;意为着机器人只会更新其地图包含距离移动基座2.5m以内的障碍物信息 obs…
阅读更多...
Python学习之用QTimer计时器实现摄像头视频的播放和暂停

Python学习之用QTimer计时器实现摄像头视频的播放和暂停

在上一篇文章《Python学习之简易视频播放器》中&#xff0c;通过python-opencv-pyqt5&#xff0c;实现了有界面的视频播放。但是&#xff0c;上文代码只有播放&#xff0c;却无法让播放的视频暂停。这是因为&#xff0c;我们在播放中使用的是while(self.cap.isOpened())循环。若…
阅读更多...
上海亚商投顾：沪指震荡调整跌0.21% 两市成交金额不足8000亿

上海亚商投顾：沪指震荡调整跌0.21% 两市成交金额不足8000亿

上海亚商投顾前言&#xff1a;无惧大盘涨跌&#xff0c;解密龙虎榜资金&#xff0c;跟踪一线游资和机构资金动向&#xff0c;识别短期热点和强势个股。 市场情绪 三大指数今日震荡调整&#xff0c;上证50午后一度跌超1%&#xff0c;以保险为首的权重板块走低。军工股逆市大涨&a…
阅读更多...
玩机搞机----电脑端几种反编译apk工具操作步骤解析

玩机搞机----电脑端几种反编译apk工具操作步骤解析

经常玩机的友友避免不了有时候需要反编译有些app或者JAR文件等等。目前各种反编译工具很多。各有所长吧。很多都是就过工具结合使用。而且很多app涉及到加密加壳。由于有些工具没有及时更新。老版本的底层还是apktool_2.4这些。对于新款的app反编译有点吃力且兼容性不太好。当然…
阅读更多...
yolov2

yolov2

yolov2相对于yolov1的改进&#xff1a; 1、加入Batch Normalization 2、yolov2使用更大的分辨率图片 V1训练使用图片分辨率为224*224&#xff0c;测试图片分辨率为448*448。 V2在V1上的改进为&#xff1a;V2训练时额外又进行了10次448*448的微调。 3、yolov2的网络结构 相…
阅读更多...
linux0.12-9-3-hd.c

linux0.12-9-3-hd.c

1、 没找到。 就是个变量。 #define DEVICE_INTR do_hd 2、 哪里用到 setup((void *) &drive_info); sys_setup [403页] 9-3 hd.c程序 9-3-1 功能描述 hd.c程序是硬盘控制器驱动程序&#xff0c;提供对硬盘控制器块设备的读写驱动和硬盘初始化处理。 程序中所有函数按照…
阅读更多...
C++ ---- 类和对象(下)

C++ ---- 类和对象(下)

目录 初始化列表 初始化列表的语法 初始化列表的特性 explicit关键字 构造函数的隐式转换 explicit的作用 static修饰成员变量和成员函数 static修饰成员变量 static修饰成员函数 友元 友元函数 友元类 内部类 匿名对象 拷贝对象时的一些编译器优化 初始化列表 …
阅读更多...
盘点 | 10大类企业管理系统有哪些

盘点 | 10大类企业管理系统有哪些

人类的发展史也是一部工具的进化史&#xff0c;企业管理手段同样不例外。移动互联网时代给了传统低下的手工操作方式致命一击&#xff0c;应运而生的各类企业管理系统工具为企业管理插上腾飞的翅膀&#xff0c;彻底颠覆了手动低效率的历史&#xff0c;变得更加移动化、智能化。…
阅读更多...
C语言——史上最全通讯录讲解（附源码）

C语言——史上最全通讯录讲解（附源码）

C语言——史上最全通讯录讲解&#xff08;附源码&#xff09; 一、开始界面的打印二、对六大板块进行定义操作三、对联系人进行初始化四、对通讯录进行初始化4.1动态版本4.2静态版本 五、通讯录六大功能的具体实现5.1判断是否需要扩容Checkcapcity5.2添加联系人ADDcontact5.3删…
阅读更多...
Salesforce许可证和版本有什么区别，购买帐号时应该如何选择？

Salesforce许可证和版本有什么区别，购买帐号时应该如何选择？

Salesforce许可证分配给特定用户&#xff0c;授予他们访问Salesforce产品和功能的权限。Salesforce版本和许可证是不同的概念&#xff0c;但极易混淆。 Salesforce版本&#xff1a;这是对组织购买的Salesforce产品和功能的访问权限。大致可分为Essentials、Professional、Ente…
阅读更多...
E-office Server_v9.0 漏洞分析

E-office Server_v9.0 漏洞分析

漏洞简介 泛微e-office是一款标准化的协同OA办公软件&#xff0c;实行通用化产品设计&#xff0c;充分贴合企业管理需求&#xff0c;本着简洁易用、高效智能的原则&#xff0c;为企业快速打造移动化、无纸化、数字化的办公平台。由于泛微 E-Office 未能正确处理上传模块中输入…
阅读更多...
解读赛力斯年报：华为智选车的B面

解读赛力斯年报：华为智选车的B面

作者 | Amy 编辑 | 德新 赛力斯&#xff0c;华为智选车的B面。 2021年&#xff0c;赛力斯SF5进入华为渠道销售&#xff0c;华为自此开启了智选车模式。到年末&#xff0c;双方更是推出AITO品牌。AITO凭借M5/M7等车型在2022年拿下了超过7.5万台的销量&#xff0c;成为增长最快的…
阅读更多...
无线模块|如何选择天线和设计天线电路

无线模块|如何选择天线和设计天线电路

无线模块的通信距离是一项重要指标&#xff0c;如何把有效通信距离最大化一直是大家疑惑的问题。本文根据调试经验及对天线的选择与使用方法做了一些说明&#xff0c;希望对工程师快速调试通信距离有所帮助。 一、天线的种类 随着技术的进步&#xff0c;为了节省研发周期&…
阅读更多...
Blender基础技巧小结（二）

Blender基础技巧小结（二）

本文续前一篇&#xff1a;Blender基础技巧小结_皮尔斯巴巴罗的博客-CSDN博客 由于2.83开始使用的是新版ui&#xff0c;但是2.83文档内并没有更新&#xff0c;所以最好参考3.3版文档 https://docs.blender.org/manual/zh-hans/3.3/interface/controls/buttons/menus.html 缩…
阅读更多...
单片机：实战练习

单片机：实战练习

目录 【1】GPIO 1.定义 2.应用 I - Input - 输入采集 O - Output - 输出控制 ​编辑​编辑 3.GPIO结构框图 4.功能描述 输入功能 输出功能 5.相关寄存器 【2】点亮一盏LED灯 1.实验步骤 2.编程实现 3.编译下载 4.复位上电 练习&#xff1a;实现LED灯闪烁…
阅读更多...
“视频AI+职业教育”会碰撞出什么样的火花？

“视频AI+职业教育”会碰撞出什么样的火花？

玩过腾讯智影、用过D-ID、体验过Vega Al&#xff0c;终于等到要出“视频AI教育”类的应用型产品了&#xff0c;很振奋。 展望&#xff1a; 已经实现AI情绪分析、AI智能审核、AI视频内容检索、AI多语言实时字幕、AI会议速记、AI窄带高清编码多种功能。 “视频AI职业教育”&#…
阅读更多...
ubantu22里面配置apache2的cgi

ubantu22里面配置apache2的cgi

在 Ubuntu 22.04 中配置 Apache2 的 CGI 1.安装 Apache2 在终端中使用以下命令安装 Apache2&#xff1a; sudo apt-get update sudo apt-get install apache22.启用 CGI 模块 在 Ubuntu 中默认情况下&#xff0c;CGI 模块是禁用的。您需要手动启用它。在终端中使用以下命令来启…
阅读更多...
为什么要使用Thrift与Protocol Buffers？

为什么要使用Thrift与Protocol Buffers？

编码数据的格式 程序通常&#xff08;至少&#xff09;使用两种形式的数据&#xff1a; 在内存中&#xff0c;数据保存在对象、结构体、列表、数组、散列表、树等中。 这些数据结构针对 CPU 的高效访问和操作进行了优化&#xff08;通常使用指针&#xff09;。如果要将数据写…
阅读更多...
centos7中安装mattermost

centos7中安装mattermost

centos7中安装mattermost 步骤如下: 第一步安装依赖项&#xff1a;在终端中执行以下命令以安装所需的依赖项 sudo yum install epel-release sudo yum install yum-utils sudo yum install wget第二步&#xff0c;下载Mattermost安装包&#xff1a;执行以下命令以下载Mattermo…
阅读更多...
PowerShell Install 二进制方式部署Python3

PowerShell Install 二进制方式部署Python3

Python 前言 Python 是一种解释型、面向对象、动态数据类型的高级程序设计语言。Python 由 Guido van Rossum 于 1989 年底发明&#xff0c;第一个公开发行版发行于 1991 年。像 Perl 语言一样, Python 源代码同样遵循 GPL(GNU General Public License) 协议。 Python downlo…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023